|
Kursprognose
Inhaltsübersicht
I. Einleitung
II. Lineare Modelle
III. Nichtlineare Modelle
IV. Entwicklung von Prognosemodellen
I. Einleitung
Unter Kursprognose versteht man die Vorhersage des zukünftigen Wertes oder dessen relative Veränderung (Renditeprognose) eines an organisierten Märkten gehandelten Titels. Mitunter beschränkt man sich auch nur auf die Vorhersage der Veränderungsrichtung (Richtungsprognose) von Kursen. Auf Finanzmärkten fallen darunter Kurse von Anleihen (Zinsprognosen), Aktien (Aktienkursprognosen), Währungen (Währungskursprognosen) und deren Derivaten (Rehkugler, H./Poddig, T. 1994).
Die Kursprognose stellt den entscheidenden Erfolgsfaktor im Asset Management dar, was sich (zumindest theoretisch) mit einem einfachen Gedankenexperiment verdeutlichen lässt: Wäre es nämlich einem Marktteilnehmer möglich, mit Sicherheit vorauszusagen, welches Anlageobjekt – bezogen auf seinen Anlagehorizont – die maximale Rendite besitzen wird, so wäre das Problem der Kapitalallokation bereits gelöst. Es müsste nur in dieses Objekt investiert werden, Fragen der Portfoliobildung wären irrelevant (Poddig, T. 1999).
Konträr zu dieser rein hypothetischen Überlegung stellt sich die aus praktischer Sicht bedeutsame Frage, ob überhaupt Kursprognosen und darauf basierende Handlungsstrategien möglich sind. Damit setzt sich die Informationseffizienzthese auseinander (Fama, 1970; Fama, 1991). Je nach Stufe der Effizienzthese wird die Sinnhaftigkeit von Prognosen generell oder in Bezug auf bestimmte Prognoseansätze negiert. Die Anwendung von Prognosetechniken impliziert damit, dass zumindest als Arbeitshypothese die Ungültigkeit bestimmter Stufen der Informationseffizienzthese (z.B. schwache oder halbstrenge) vorausgesetzt wird. Der Nachweis nachhaltig erzielbarer, systematischer Extragewinne bei Anwendung der jeweiligen Prognosetechnik würde damit zugleich eine Bestätigung der Arbeitshypothese und Falsifizierung der entsprechenden Stufe der Informationseffizienz darstellen (Rehkugler, H./Poddig, T. 1991).
In der Praxis werden die verschiedenen Prognoseansätze nach ihrer Herkunft in Verfahren der Technischen (Wertpapier-)Analyse, der Fundamentalanalyse und der quantitativen Analyse unterschieden. Die Technische Analyse geht von der Vorstellung aus (Pring, M.J. 1985), dass letztlich alle bewertungsrelevanten Informationen im Kurs abgebildet werden, jedoch erst allmählich im Rahmen eines langsamen Diffusionsprozesses. Dabei bilden sich typische Muster in den Kursverläufen heraus, welche sich für Prognosen nutzen lassen. Traditionelles Instrument ist hier die Chartanalyse, welche auf Basis einer „ visuellen Mustererkennung “ Aussagen über die zukünftige Veränderungsrichtung eines Kurses ableitet. Mittels der Technischen Indikatoren (z.B. Gleitende Durchschnitte) wird eine Operationalisierung der grundlegenden Ideen hinter der Chartanalyse angestrebt. Die Fundamentalanalyse geht von der Vorstellung eines „ inneren Wertes “ eines Finanztitels aus (Loistl, O. 1992). Dieser ist das Resultat der dahinter stehenden ökonomischen Bestimmungsgrößen. So ergibt sich der Wert einer Aktie z.B. aus dem Wert des zugehörigen Unternehmens. Jener Wert wird wiederum von dessen zukünftiger Ertragskraft bestimmt, welche von Größen wie Marktstellung, Produktprogramm, Forschung und Entwicklung oder Fähigkeiten des Managements beeinflusst wird. Die Fundamentalanalyse besitzt enge Bezüge zur Unternehmensbewertung. Eines ihrer wesentlichen Instrumente ist die Jahresabschlussanalyse. Die Technische Analyse wertet im Wesentlichen allein die vergangene Kurshistorie aus, um Prognosen über den zukünftigen Kursverlauf abzuleiten. Die Fundamentalanalyse betrachtet (zusätzlich) alle öffentlich verfügbaren Informationen über einen Finanztitel. Unter quantitativer Analyse wird der Einsatz mathematisch-statistischer Verfahren in der Finanzanalyse allgemein verstanden. Hier handelt es sich z.B. um Verfahren der Zeitreihenanalyse (z.B. ARIMA-Modelle), der Ökonometrie (z.B. Regressionsmodelle) oder der Künstlichen Intelligenz (z.B. Neuronale Netze). Diese in der Praxis gebräuchliche (traditionelle) Unterscheidung ist dabei eher historisch gewachsen. Unterscheidet man die grundlegenden Ansätze nach ihrer benutzten Informationsbasis, so könnte man alle zeitreihenanalytischen Verfahren, die allein auf der Analyse der vergangenen Kurshistorie basieren, der Technischen Analyse und alle anderen quantitativen Verfahren der Fundamentalanalyse zuordnen. Die eigenständige Kategorie der quantitativen Analyse ist insofern unnötig. Aufgrund der weiten Verbreitung in der Praxis soll die oben eingeführte traditionelle Systematisierung jedoch beibehalten und im Folgenden die quantitative Analyse näher betrachtet werden.
Bei den Prognosetechniken werden subjektive und objektive Verfahren unterschieden (Hüttner, M. 1982). Bei den subjektiven Verfahren handelt es sich z.B. um die Befragung von Experten, deren Urteil die Prognose darstellt (z.B. Delphi-Methode). Aber auch Verfahren, bei denen ein erhebliches subjektives Element seitens des Analysten mit einfließt (z.B. bei der Chartanalyse oder bei der Interpretation von Unternehmenskennzahlen im Zuge der Fundamentalanalyse), können hierzu gezählt werden. Unter den objektiven Verfahren wird die Anwendung mathematisch-statistischer Analyseverfahren verstanden. Da sie klar definiert sind, ist nach der Festlegung der jeweiligen Vorgehensweise die resultierende Prognose objektiv nachvollziehbar. Die Technische Analyse und die Fundamentalanalyse (im Sinne des oben skizzierten traditionellen Verständnisses) lassen sich also bei weit gefasster Interpretation den subjektiven, die quantitative Analyse den objektiven Verfahren zuordnen.
Die Verfahren der quantitativen Analyse lassen sich weiterhin nach der Art ihres grundlegenden methodischen und (bei der Analyse von Finanzmärkten) ökonomischen Ansatzes unterscheiden (Poddig, T./Rehkugler, H./Jandura, D. 1994; vgl. Abb. 1 in Anlehnung an Poddig, T. 1996). Hinsichtlich des methodischen Ansatzes werden hier lineare (z.B. die Regressionsanalyse) von nichtlinearen Verfahren (z.B. ARCH/GARCH-Modelle) unterschieden. Speziell bei der Analyse und Prognose von Finanzmärkten (statt Einzeltiteln) stellt sich die Frage, ob man den zu prognostizierenden Markt im Rahmen der Modellbildung eher isoliert betrachtet (Partialansatz) oder ob man zusätzlich die Interaktion mit anderen Finanzmärkten mit berücksichtigt (Simultanansatz).
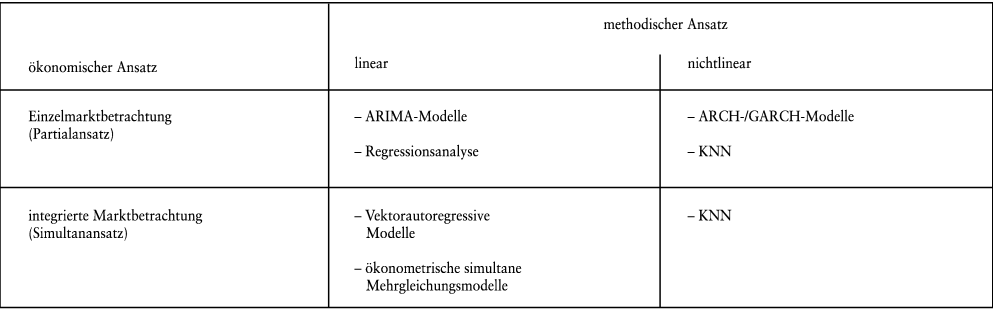
Abb. 1: Systematisierung der quantitativen Verfahren
In Abb. 1 sind einige wenige ausgewählte Verfahren, die nachfolgend näher betrachtet werden, den jeweiligen Quadranten zugeordnet. Aufgrund des sehr beschränkten Umfangs dieses Stichworts ist diese Übersicht weder erschöpfend noch vollständig. Die folgenden Betrachtungen verstehen sich daher auch als rein exemplarisch.
II. Lineare Modelle
1. ARIMA-Modelle
Die ARIMA-Modelle sind den zeitreihenanalytischen Verfahren zuzuordnen (Granger, C.W.J./Newbold, P. 1986; Loistl, O. 1992). Sie erklären in allgemeinster Form die Realisationen yt einer Zeitreihe als gewichtete Summe p früherer Realisationen (AR(p)-Prozess) und q vergangener Zufallsereignisse (MA(q)-Prozess).

Das Modell nach (1) wird als ARMA(p,q)-Prozess bezeichnet. Für die Beschreibung einer Zeitreihe yt durch einen ARMA(p,q)-Prozess muss diese zumindest schwach stationär sein. Eine Zeitreihe heißt dann (schwach) stationär, wenn (a) der Erwartungswert E(yt), (b) die Varianz Var(yt) und (c) alle Autokorrelationskoeffizienten ρk(yt) vom Zeitindex t unabhängig sind (Schlittgen, R./Steitberg, B.H.J. 1995). Da Kursreihen in aller Regel trendbehaftet sind, ist diese Voraussetzung nicht gegeben. Durch einfache (d = 1) oder mehrfache Differenzenbildung kann jedoch eine nicht stationäre Zeitreihe in eine stationäre überführt werden:
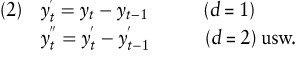
Die Modellierung nach (1) erstreckt sich dann auf die transformierte Zeitreihe. Bei der späteren Prognose ist der tatsächlich zu prognostizierende (Kurs-)Wert durch Rückrechnung ( „ integrating “ ) zu ermitteln. Man spricht deshalb auch von einem AR-Integrated-MA-Modell (kurz ARIMA(p,d,q)-Modell).
Die Verwendung (schwach) stationärer Reihen ist im Übrigen bei den meisten quantitativen Verfahren strenge Anwendungsvoraussetzung. Mitunter ist außerdem in Kursreihen ein exponenzieller Trend enthalten, der sich durch einfache Differenzenbildung nicht beseitigen lässt. Im Allgemeinen logarithmiert man daher zunächst die Kurs- bzw. Indexreihen und bildet dann erst die ersten Differenzen (sog. Log-Differenzen). Diese stellen zugleich stetige Renditen dar und besitzen somit eine leichte Interpretierbarkeit. Im Regelfall werden in der quantitativen Analyse also Renditeprognosen erstellt, aus denen sich erst durch Rückrechnung die eigentlichen Kurse bzw. Indexstände ergeben. Ohne es im Folgenden explizit zu erwähnen, wird vorausgesetzt, dass die Log-Differenzenbildung zur Stationarisierung einer Zeitreihe führt.
Nach der Stationarisierung der originären Kursreihe sind die Parameter p und q des die transformierte Reihe erklärenden ARMA-Prozesses zu ermitteln, was man als Phase der Modellidentifikation bezeichnet. Dieser schwierige Schritt lässt sich mittels grafischer Analysen oder durch ein aufwändiges, systematisches Testverfahren vollziehen. Im folgenden Schritt der Parameterschätzung werden nun anhand der Zeitreihe die Werte der Koeffizienten ϕi und φi geschätzt. Dies kann mit Hilfe der Kleinste-Quadrate Methode (bei reinen AR-Modellen) oder über die Lösung von Yule-Walker-Gleichungen erfolgen.
Damit verfügt man über die vermutliche Struktur des Datengenerierungsprozesses, einschließlich dessen geschätzter Koeffizienten. Der eigentlichen Prognose ist noch eine Phase der Modelldiagnose vorgeschaltet. Hier wird noch einmal überprüft, ob es ernsthafte Zweifel an der Gültigkeit des geschätzten Modells gibt. Sollte dies der Fall sein, ist zur Phase der Modellidentifikation zurückzugehen und eine andere Spezifikation des zu Grunde liegenden ARMA(p,q)-Prozesses vorzunehmen. Hält das geschätzte Modell dagegen der Modellüberprüfung stand, kann zur eigentlichen Prognose zukünftiger Werte übergegangen werden. Sie ergibt sich unmittelbar als schlichte Fortschreibung der Gleichung (1), indem der aktuelle Zeitpunkt t als t-1 und die Prognose für t+1 als t im Sinne von (1) interpretiert wird.
2. Die lineare Regression
Die lineare multiple Regression versucht, den Wert einer Zeitreihe yt zum Zeitpunkt t in Abhängigkeit von n (zeitverzögerten) exogenen Einflussgrößen xi,t-L zum Zeitpunkt t-L (L = Zeitverzögerung) zu erklären (Griffiths, W.E./Hill, R.C./Judge, G.G. 1993; Greene, W.H. 1997). Sie unterstellt dabei einen linearen funktionalen Zusammenhang und besitzt folgende Form:

Für eine unbedingte Prognose müssen die Einflussgrößen xi mit einer Zeitverzögerung L > 0 eingehen. Aus Vereinfachungsgründen wurde dabei in (3) eine einheitliche Zeitverzögerung L für alle n Einflussgrößen unterstellt. Diese kann jedoch auch je nach Einflussgröße unterschiedlich gewählt werden. Eine bedingte Prognose liegt dagegen vor, wenn für die Zeitverzögerung L = 0 gewählt wird. Bei individuellen Zeitverzögerungen liegt eine bedingte Prognose bereits dann vor, wenn diese Bedingung schon für eine Einflussgröße erfüllt ist. Während unbedingte Prognosemodelle eine Prognose auf Basis heute verfügbarer Informationen erlauben, besteht der Nachtteil bedingter Prognosemodelle darin, zunächst Prognosen aller Einflussgrößen zu erfordern, bevor die eigentlich interessierende Zielgröße vorhergesagt werden kann.
Ziel der Regressionsanalyse ist es, die Koeffizienten βi aus einer Reihe vorliegender Beobachtungen der Werte der Einflussgrößen xi und dem daraufhin eingetretenen Wert von y so zu schätzen, dass die quadrierte Differenz zwischen tatsächlich eingetretenem und vorhergesagtem Wert über alle Beobachtungen (Fehlerfunktion) minimal wird.

Wichtige Prämissen der Regressionsanalyse sind die lineare Beschreibbarkeit des Prognoseproblems, die „ white noise “ Eigenschaften der Störgröße εt und die lineare Unabhängigkeit der Einflussgrößen xi untereinander. Ist letztere Bedingung verletzt, liegt Multikollinearität vor, die zu erheblichen Problemen bei der Schätzung der βi führt. Sie erweisen sich dann auch als stark sensitiv gegenüber Datenänderungen (etwa beim Hinzunehmen weiterer Beobachtungen). Um dieses Problem im Vorfeld zu erkennen, kann eine Korrelationsanalyse der Einflussgrößen vorgenommen werden.
Setzt man in (3) x1=yt-1, x2=yt-2 usw., so entsteht offensichtlich ein AR(n)-Modell. Das Regressionsmodell kann also durch geeignete Interpretation der Einflussgrößen in ein reines Zeitreihenmodell überführt werden, auch wenn dies von der Regressionsanalyse eigentlich nicht intendiert wird. Ebenso ist ein „ Mischmodell “ aus einem Zeitreihen- und einem Regressionsmodell mit exogenen Einflussfaktoren möglich. In (5) wird z.B. yt aus seinen eigenen letzten k vergangenen Realisationen (AR(k)-Prozess) und aus den letzten k Realisationen einer exogenen Einflussgröße x erklärt.
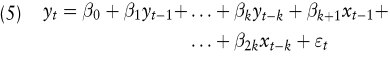
3. Vektorautoregressive Modelle
Die exemplarisch betrachteten ARIMA-Modelle und das Regressionsmodell eignen sich für die Modellierung eines Finanzmarktes, sofern dieser isoliert betrachtet wird (vgl. linker oberer Quadrant in Abb. 1). Um jedoch einen Marktverbund (z.B. die Aktienmärkte mehrerer Länder zusammen) zu modellieren und prognostizieren, werden komplexere Modelle benötigt (vgl. linker unterer Quadrant in Abb. 1). Vektorautoregressive Modelle (VAR-Modelle) gehören zu den einfacheren unter ihnen (Hamilton, J.D. 1994). Um sie kurz zu illustrieren, sei das Modell nach (5) als Ausgangspunkt herangezogen. Zusätzlich sei aber angenommen, dass auch xt Werte eines interessierenden und gleichzeitig zu prognostizierenden anderen Finanzmarktes darstelle. Das (vektorautoregressive) Modell des Marktverbundes ist in (6) dargestellt.
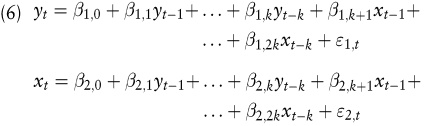
Bei größeren vektorautoregressiven Modellen wird die in (6) gewählte Notation schnell unübersichtlich. Man schreibt (6) daher üblicherweise in Matrizennotation.

Vektorautoregressive Modelle können zugleich als Hybridansatz aus Methoden der technischen und fundamentalen Analyse angesehen werden. Stellt z.B. in (6) yt die Rendite des DAX und xt die Rendite des Dow Jones zum Zeitpunkt t dar, dann wird der DAX zum einen aus der eigenen Renditehistorie ( „ technischer Ansatz “ ) und zum anderen aus der Renditehistorie des Dow Jones ( „ fundamentaler Ansatz “ ) prognostiziert. Natürlich würde dies im Beispiel ebenso für xt (die Rendite des Dow Jones) in analoger Weise gelten. VAR-Modelle können außer als Prognoseinstrument auch zur Analyse des Verhaltens ökonomischer Systeme eingesetzt werden. Ein Beispiel sind hier Impulsantwortanalysen zur Untersuchung der Wirkung von Schocks auf das ökonomische System (wie z.B. ein System von Aktien-, Renten- und Devisenmärkten auf Zinsänderungen reagiert).
In (6) (bzw. (7)) kommen in jeweils einer Gleichung neben autoregressiven Komponenten nur verzögerte Werte von endogenen Variablen jeweils anderer Gleichungen als exogene Variablen vor. Würde man in der ersten Gleichung von (6) die Variable xt und in der zweiten Gleichung die Variable yt zusätzlich als unabhängige Variablen auf der jeweils rechten Seite einsetzen, würde ein simultanes Mehrgleichungsystem entstehen (simultaneous equation model, SEM). SEM gehen weiter als VAR-Modelle, indem sie zusätzlich die zeitgleichen Wechselwirkungen aller betrachteten Variablen des Gleichungssystems untereinander in die Modellierung mit einbeziehen. Sie entsprechen in idealer Weise der Vorstellung integrierter Finanzmärkte, auf denen sich die Preisbildungsprozesse auf den einzelnen nationalen Teilmärkten in Wechselwirkung mit denen anderer Märkte vollziehen. Ferner können bei der Schätzung eines SEM die in den Beobachtungsdaten enthaltenen Informationen effizienter als bei der Schätzung von VAR-Modellen genutzt werden. Für die Schätzung von SEM können verschiedene, teilweise mathematisch sehr komplexe Verfahren herangezogen werden. In der praktischen Anwendung verbinden sich mit ihnen allerdings vielfältige Detailprobleme. Schätzverfahren und Anwendungsprobleme können hier aus Platzgründen nicht näher diskutiert werden. Sie führen jedoch bei vielen Anwendungen dazu, dass der Einsatz von SEM als impraktikabel abgelehnt wird.
VAR-Modelle sind dagegen keine SEM, da jede einzelne Modellgleichung unabhängig von allen anderen ist (vgl. (6)). Sie werden deshalb im Regelfall auch unabhängig voneinander mittels des Verfahrens der Kleinsten-Quadrate einzeln geschätzt. Insofern handelt es sich hier um einen „ Verbund unabhängiger Regressionsmodelle “ . Aufgrund der Komplexität von SEM und den damit verbundenen Problemen werden VAR-Modelle dennoch gerne als „ Ersatzlösung “ für die Modellierung, Analyse und Prognose eines Marktverbundes herangezogen. Ein wesentliches Problem von VAR-Modellen besteht bei der praktischen Anwendung oftmals in der hohen Anzahl freier Parameter. So sind z.B. bei einem VAR-System mit n = 3 Zeitreihen und einer Lagordnung von k = 3 schon 3 · (3 · 3 + 1) = 30 Koeffizienten zu schätzen. VAR-Systeme neigen schnell zur Überanpassung (vgl. Abschnitt IV.4.).
III. Nichtlineare Modelle
1. ARCH/GARCH-Modelle
Im rechten oberen Quadranten der Abb. 1 werden quantitative Verfahren betrachtet, welche es erlauben, Nichtlinearitäten in den Preis- bzw. Renditegenerierungsprozessen von Finanztiteln zu berücksichtigen. Unter den Partialansätzen sind insbesondere die ARCH/GARCH-Modelle hervorzuheben, die in der Finanzanalyse nachhaltige Beachtung gefunden haben (Engle, R.F. 1982; Bollerslev, T. 1986). Sie sollen stellvertretend für jenen Quadranten vorgestellt werden. Zur Illustration sei auf den AR(p)-Prozess aus Gleichung (1) zurückgegriffen (der MA(q)-Prozess in (1) sei hier vernachlässigt). Als wesentliche Voraussetzung zur Erklärung und Prognose einer Zeitreihe yt durch einen AR(p)-Prozess wird dort von der Stationarität der Zeitreihe yt, d.h. u.a. der Varianzstationarität von yt, ausgegangen. Nun weisen jedoch die Varianzen empirisch beobachtbarer Renditeverläufe einen anscheinend zeitabhängigen Verlauf auf, wobei Phasen hoher Varianzen der Renditen (Phasen hoher „ Volatilität “ ) und Phasen niedriger Varianzen einander abwechseln. Diese sich ständig ändernde Varianz der Zeitreihe yt besitzt im hier interessierenden Kontext der Kurs- bzw. Renditeprognose zwei wichtige Aspekte. Zum einen kann die Modellierung und Prognose der Varianz (Volatilität) selbst eine eigenständige Bedeutung besitzen. Innerhalb der Optionspreistheorie stellt etwa die Volatilität der Rendite eines Finanztitels den zentralen Parameter zur Findung des „ fairen “ Preises einer Option auf diesen Titel dar. Damit kann die Modellierung und Prognose der Volatilität schon für sich allein eine wichtige Aufgabe für praktische Anwendungen darstellen. Zum anderen führt aber eine sich ändernde Varianz zu einer verschlechterten Schätzung der Koeffizienten des AR(p)-Prozesses nach (1). ARCH/GARCH-Modelle erlauben Volatilitätsprognosen und eine verbesserte Koeffizientenschätzung. Zur Illustration eines ARCH-Modells sei nun in Gleichung (1) (gedanklich) die Störgröße εt durch die Störgröße ut ersetzt, welche keinen „ white noise “ Prozess mehr darstellt. Dann wird im nächsten Schritt die Zeitreihe der Störgröße ut selbst mit (8) und (9) modelliert.

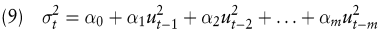
Die Folge der Störgröße ut in (8) wird damit selbst als eine Art autoregressiver Prozess modelliert und als autoregressive conditional heteroskedastic process der Ordnung m bezeichnet (ut?ARCH(m)). Ein ARCH-Modell besteht damit aus zwei Teilen, nämlich (i) dem Modell der Zeitreihe yt (etwa als AR-Modell nach (1) oder als lineares Regressionsmodell) und (ii) dem Modell der Störgröße ut in Form eines autoregressiven konditionalen heteroskedastischen Prozesses (z.B. nach (8) in Verbindung mit (9)). Die Schätzung eines ARCH-Modells kann in Form einer vierstufigen Prozedur erfolgen, die letztlich zu einer durch die Heteroskedastizität von ut (und damit von yt) bedingten und notwendigen Korrektur der Schätzung der Koeffizienten ϕi gegenüber der einer gewöhnlichen Kleinste-Quadrate Schätzung von (1) führt.
Bei der Erweiterung des ARCH-Modells zum GARCH-Modell werden bei der Modellierung der Varianz des Störterms ut nicht nur die Realisationen vergangener Schocks ut-1, ut-2, ut-3 usw. berücksichtigt, sondern ebenfalls die historische (bedingte) Varianz σ2t-1, σ2t-2, σ2t-3 usw. Mit dieser zusätzlichen Berücksichtigung ergibt sich (10) in Erweiterung von (9):
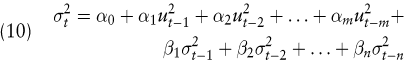
Entsprechend wird nun von einem GARCH(n,m)-Modell gesprochen.
2. Künstliche Neuronale Netzwerke
Künstliche Neuronale Netzwerke (KNN) sind insbesondere im rechten oberen und rechten unteren Quadranten der Abb. 1 einzuordnen. Sie dienen originär innerhalb der Künstlichen Intelligenz zur Erforschung der Arbeitsweise natürlicher neuronaler Netzwerke und zur ingenieurmäßigen Umsetzung von deren Leistungspotenzial. Sie haben mittlerweile aber auch bei ökonomischen Anwendungen Einzug gehalten, vornehmlich im Bereich der Kursprognosen. KNN ist ein Sammelbegriff, der etwa 20 bis 30 verschiedenartige Typen umfasst, teilweise in zahlreichen Untervarianten (Rehkugler, H./Kerling, M. 1995). Im Folgenden sei daher nur der bisher bei Kursprognosen meist verwendete Typ, das Multilayer-Perceptron (MLP), skizziert (vgl. Abb. 2). 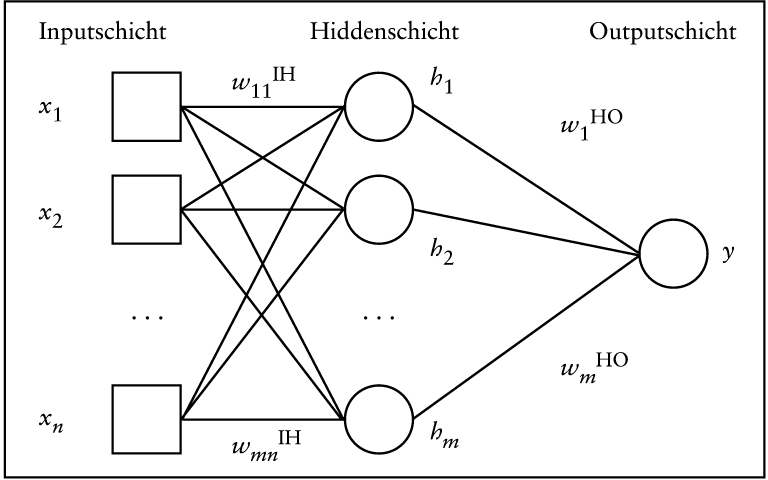
Abb. 2: Ein Neuronales Netz (Multilayer-Perceptron)
Die Abb. 2 stellt eine einfache Grundvariante eines dreilagigen MLP mit einer Input-, einer Hidden- und einer Outputschicht dar. Die Anzahl der Zwischenschichten und der Verarbeitungseinheiten (in Abb. 2 durch Kreise symbolisiert) auf den einzelnen Schichten ist problemabhängig. Die Arbeitsweise des abgebildeten Modells lässt sich wie folgt beschreiben: An die Inputschicht werden die Werte der Einflussgrößen xi angelegt. Diese Werte werden nun von jeder Verarbeitungseinheit der Zwischenschicht gewichtet und durch Summation zu einem Nettoeingangssignal zusammengefasst. Dieses führt nach einer nichtlinearen Transformation zum Ausgangssignal hi einer Verarbeitungseinheit auf der Zwischenschicht. Die Verarbeitungseinheit der Outputschicht gewichtet ihrerseits die Ausgangssignale der Zwischenschicht und fasst sie durch Summation zu einem Nettoeingangssignal zusammen (ggf. wendet sie hierauf wiederum eine nichtlineare Transformation an).
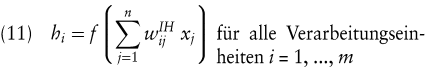

Vergleicht man das hier grob skizzierte Modell mit dem einfachen linearen Regressionsmodell nach (3), so sind gewisse Parallelen erkennbar (Poddig, T./Huber, C. 1998). Innerhalb der Transformationsfunktionen f bzw. g in (11) bzw. (12) erfolgen lediglich Linearkombinationen von Eingangsgrößen, genauso wie beim Regressionsmodell. Die Erweiterung besteht hier „ nur “ in der nachfolgenden nichtlinearen Transformation und der mehrfachen Wiederholung dieses Vorgangs mittels verschiedener Verarbeitungseinheiten. Grob vereinfacht lässt sich das in Abb. 2 dargestellte MLP als „ mehrstufiges Regressionsverfahren mit nichtlinearen Transformationen “ umschreiben. Durch diese mehrstufige Verarbeitung und nichtlineare Transformation der Eingangsgrößen xi können beliebige funktionale Zusammenhänge approximiert werden, was die besondere Mächtigkeit dieses Analyseinstruments ausmacht. Wie auch bei den vorangegangenen Verfahren sind die Werte der Gewichte (diese entsprechen inhaltlich den Koeffizienten der vorangegangenen Verfahren) zunächst unbekannt und müssen anhand von Beobachtungen der Vergangenheit geschätzt werden. Dieser Schätzprozess stellt eine besondere Problematik dar. Während bei den vorangegangenen Verfahren eindeutige Lösungen zur Schätzung der Koeffizienten aus den vorliegenden Beobachtungen existieren, ist dies hier nicht der Fall. Aufgrund der Nichtlinearität des MLP kann nämlich nicht mehr analytisch und eindeutig die Lage des globalen Minimums der Fehlerfunktion bestimmt werden. Die Werte der Gewichte werden vielmehr durch eine langwierige, iterative Schätzprozedur approximiert ( „ Lernen “ eines KNN), die durchaus in lokalen Minima der Fehlerfunktion enden kann. Dann würde aber das MLP bei späteren Prognosen nur suboptimal arbeiten.
Dem besonderen Leistungspotenzial der KNN stehen eine Vielzahl anderer, teilweise erheblicher Probleme gegenüber. Vor diesem Hintergrund ist oftmals die Anwendung der vorher dargestellten Verfahren weitaus einfacher und im praktischen Einsatz nicht immer schlechter.
IV. Entwicklung von Prognosemodellen
Zur Lösung eines konkreten Prognoseproblems ist neben der Auswahl des problemadäquaten Verfahrens (vgl. auch Abb. 1) dessen sachgerechte Anwendung mindestens ebenso entscheidend für den Erfolg. Praktische Erfahrung zeigt deutlich, dass z.B. bei sorgfältiger und gewissenhafter Anwendung der Regressionsanalyse weitaus bessere Prognoseergebnisse erzielt werden als beim unsachgemäßem Einsatz von KNN, obwohl sie der Regressionsanalyse vom Leistungspotenzial her weitaus überlegen sind. Zur Entwicklung eines leistungsfähigen Prognosemodells haben sich verschiedene, verfahrensunabhängige Prinzipien und Vorgehensweisen bei der Modellentwicklung bewährt (Poddig, T./Huber, C. 1998; Kerling, M. 1998; Poddig, T. 1999). Aus Platzgründen können die dabei zu beachtenden Aspekte nur genannt, jedoch nicht tiefer diskutiert werden.
1. Zusammenstellung und Vorbereitung der Daten
Der erste wichtige Schritt besteht in der geeigneten Definition der zu prognostizierenden Zielgröße. Ferner sind zusätzlich potenzielle Einflussgrößen in Bezug auf die Zielgröße zu identifizieren. Da die meisten der später einzusetzenden Verfahren stationäre Zeitreihen voraussetzen, ökonomische Zeitreihen in aller Regel jedoch trendbehaftet sind, sind sie in „ Rohform “ nicht verwendbar. Neben der zumeist erforderlichen (Log-) Differenzenbildung der Zeitreihen können weitere Datenvortransformationen erforderlich sein, um z.B. Ausreißer zu beseitigen. Ein in der praktischen Anwendung oftmals schwieriges Problem ist der Umgang mit fehlenden Daten ( „ missing values “ ).
2. Analyse der Problemstruktur und Wahl des geeigneten Instruments
Die Zielgröße sollte im Vorfeld der eigentlichen Modellierung mittels linearer und nichtlinearer Testverfahren auf vorhandene Strukturen (in Bezug auf die eigene Historie und in Bezug auf mögliche exogene Einflussfaktoren) untersucht werden. Sind nämlich trotz des Einsatzes fortgeschrittener, auch nichtlinearer Testverfahren keine Strukturen identifizierbar, besteht wenig Aussicht auf eine erfolgreiche Prognose. Ferner sind in dieser Phase wesentliche Grundsatzentscheidungen, insbesondere basierend auf den Ergebnissen der Testverfahren, zu treffen. Exemplarisch seien die Auswahl des (i) geeigneten Verfahrens, (ii) Typs der Prognose (bedingt vs. unbedingt) oder (iii) Festlegung des Prognosehorizonts genannt.
3. Vorselektion der relevanten Einflussgrößen
In diesem Schritt geht es um die gezielte Auswahl der im Modell zu verwendenden Variablen. Da man oftmals als Ergebnis der vorhergehenden Schritte über eine Vielzahl an möglichen Einflussgrößen verfügt, sollte der Datenpool zunächst um Redundanzen bereinigt werden. Mittels Korrelations- oder Faktorenanalyse lassen sich Variablen mit ähnlichem Informationsgehalt identifizieren und ggf. aussondern. Alternativ oder ergänzend kann der verbleibende Datenpool auf wenige (synthetische) Faktoren, ebenfalls mittels einer Faktorenanalyse, verdichtet werden (Datenkompression). Im letzten Teilschritt sind die relevanten Einflussfaktoren unter Verwendung geeigneter Testverfahren zu identifizieren.
4. Spezifikation, Schätzung und Postprocessing des Prognosemodells
Nach der Identifikation der wahrscheinlich relevanten Einflussgrößen sind die (vorläufig) endgültige Spezifikation des Prognosemodells vorzunehmen und dessen Koeffizienten anhand der Beobachtungsdaten zu schätzen. Vor der realen Anwendung des Modells ist es jedoch sorgfältig zu überprüfen. Unter Postprocessing sind hier eine erste Modelldiagnose anhand statistischer Testverfahren und die Validierung an Testdaten zu verstehen, die schon vor dem Beginn der Modellbildung ausgesondert und bisher nicht benutzt wurden. Wegen der besonderen Bedeutung des Validitätstests soll dieser etwas näher ausgeführt werden.
Die Hauptursache für unbefriedigende Prognoseleistungen ist nämlich nicht immer die vermeintliche und schnell herangezogene Erklärung, dass in der Vergangenheit beobachtete Zusammenhänge sich eben nicht auf die Zukunft übertragen ließen. Vielmehr liegt die schlechte Prognoseleistung oftmals in der Überanpassung (Overfitting) der Modelle auf die Schätzperiode begründet. Unerfahrene Analysten versuchen mitunter, eine möglichst hohe Anpassungsgüte der Modelle auf den Beobachtungsdaten zu erreichen. Dem liegt der Trugschluss zu Grunde, dass die Prognosegüte eines Modells umso höher sei, je besser es auf die Verhältnisse der Schätzperiode abgestimmt ist. Aber allein durch die Erhöhung der Anzahl an Einflussgrößen (auch sinnloser!) gelingt für die Schätzperiode eine immer bessere Anpassung des Modells, da zunehmend Scheinzusammenhänge die Güte der Anpassung steigern. Dadurch sinkt aber gleichzeitig die Prognoseleistung des Modells auf unbekannten Daten.
Zur Erkennung von Überanpassungen wird der Schätzzeitraum zerlegt, indem aus ihm zufällige Zeitpunkte oder ganze Zeitabschnitte mit ihren zugehörigen Daten ausgesondert werden (Validierungsmenge). Der oben skizzierte Prozess der Modellentwicklung findet jetzt nur noch auf den verbleibenden Daten (Trainingsmenge) statt. Nach der Schätzung des Prognosemodells und einer ersten Modelldiagnose wird es dann an der Validierungsmenge getestet. Zeigt das Prognosemodell schon hier unbefriedigende Prognoseleistungen, hat es offensichtlich nicht die für den Beobachtungszeitraum relevanten Zusammenhänge abgebildet. Dann ist das Prognosemodell anders zu spezifizieren und der gesamte Entwicklungsprozess mit der neuen Spezifikation zu wiederholen.
5. Fiktive Anwendung des Modells und Test gegen eine Benchmark
Wenn das Modell die Validierung erfolgreich durchlaufen hat, sollte der fiktive Einsatz des Modells anhand realer Daten simuliert werden. Diese können ebenfalls ganz zu Beginn der Modellentwicklung ausgesondert worden sein oder es handelt sich hier bereits um „ Echtzeitdaten “ . Um die Güte des Modells beurteilen zu können, sollte ein Referenzmodell (Benchmark) herangezogen werden. Eine einfache Benchmark ist z.B. die naive Prognose, welche den zuletzt beobachteten Wert einer Zeitreihe als Schätzer für den folgenden benutzt. Kann das Prognosemodell in diesem abschließenden Test nicht die Benchmark überbieten, liegt möglicherweise ein Strukturbruch vor. Mitunter kann aber eine erneute Änderung der Modellspezifikationen (etwa ein kompletter Austausch der hypothetischen Einflussgrößen) zu einem robusteren Modell führen.
Literatur:
Bollerslev, T. : Generalized Autoregressive Conditional Heteroskedasticity, in: Journal of Econometrics 1986, No. 31, S. 307 – 327
Engle, R.F. : Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation, in: Econometrica 1982, No. 4, S. 987 – 1007
Fama, E.F. : Efficient Capital Markets: A Review of Theory and Empirical Work, in: JF 1970, S. 383 – 417
Fama, E.F. : Efficient Capital Markets: II, in: JF 1991, S. 1575 – 1617
Granger, C.W.J./Newbold, P. : Forecasting Economic Time Series, 2. A., Orlando 1986
Greene, W.H. : Econometric Analysis, 3. A. (International Edition), New York 1997
Griffiths, W.E./Hill, R.C./Judge, G.G. : Learning and Practicing Econometrics, New York 1993
Hamilton, J.D. : Time Series Analysis, Princeton, New Jersey 1994
Hüttner, M. : Markt- und Absatzprognosen, Stuttgart 1982
Kerling, M. : Moderne Konzepte der Finanzanalyse – Markthypothesen, Renditegenerierungsprozesse und Modellierungswerkzeuge, Bad Soden/Ts. 1998
Loistl, O. : Computergestütztes Wertpapiermanagement, 4. A., München, 1992
Poddig, T./Huber, C. : Renditeprognosen mit Neuronalen Netzen, in: Handbuch Portfoliomanagement, hrsg. v. Kleeberg, J.M./Rehkugler, H., Bad Soden/Ts. 1998, S. 349 – 384
Poddig, T./Rehkugler, H./Jandura, D. : Ein „ Weltmodell “ integrierter Finanzmärkte, in: Neuronale Netze in der Ökonomie, hrsg. v. Rehkugler, H./Zimmermann, H.G., München 1994, S. 337 – 425
Poddig, T. : Analyse und Prognose von Finanzmärkten, Bad Soden/Ts. 1996
Poddig, T. : Handbuch Kursprognose, Quantitative Methoden im Asset Management, Bad Soden/Ts. 1999
Pring, M.J. : Technical analysis explained, New York 1985
Rehkugler, H./Kerling, M. : Einsatz Neuronaler Netze für Analyse- und Prognose-Zwecke, in: BFuP 1995, H. 3, S. 306 – 324
Rehkugler, H./Poddig, T. : Künstliche Neuronale Netze in der Finanzanalyse: Eine neue Ära der Kursprognosen?, in: WI 1991, H. 5, S. 365 – 374
Rehkugler, H./Poddig, T. : Kurzfristige Wechselkursprognosen mit Künstlichen Neuronalen Netzwerken, in: Finanzmarktanwendungen neuronaler Netze und ökonometrischer Verfahren, hrsg. v. Bol, G./Nakhaeizadeh, G.//Vollmer, K.-H., Heidelberg 1994, S. 1 – 24
Schlittgen, R./Steitberg, B.H.J. : Zeitreihenanalyse, 6. A., München 1995
|