|
Losgröße
Inhaltsübersicht
I. Die Losgrößenplanung als Teil der Produktionsplanung
II. Entscheidungsrelevante Kosten bei der Losgrößenbestimmung
III. Das Grundmodell der Losgrößenplanung
IV. Einstufige Losgrößenmodelle mit endlicher Lagerauffüllgeschwindigkeit
V. Mehrstufige Modelle
VI. Simultanplanung von Losmenge und Lossequenz
VII. Kapazitätsbeschränkungen in Losgrößenmodellen
VIII. Reduzierung der Losgrößen durch Rüstkostensenkung
I. Die Losgrößenplanung als Teil der Produktionsplanung
In der Produktionsplanung stellt sich neben dem Problem der Planung des qualitativen und quantitativen Produktionsprogramms die Frage, in welcher Weise die Produktion durchgeführt (Durchführungs-, Prozessplanung) und wie die hierfür erforderlichen Produktionsfaktoren bereitgestellt (Bereitstellungsplanung) werden sollen. Damit wird auch die Frage aufgeworfen, wie viele Einheiten eines Gutes als zusammenhängender Posten (Los) beschafft (Beschaffungslosgröße) bzw. gefertigt (Fertigungslosgröße) werden sollen und wann diese herzustellen sind.
Das Problem der Bestimmung von (optimalen) Los- bzw. Auftragsgrößen ergibt sich immer dann, wenn weder die einmalige noch die bedarfssynchrone Beschaffung oder Fertigung von Gütern zur Deckung des auftretenden Bedarfs möglich oder wirtschaftlich ist.
Während sich das Problem der Ermittlung optimaler Beschaffungslosgrößen grundsätzlich bei allen denkbaren Produktionstypen und Nachfragestrukturen stellen kann, gewinnt das Problem der Ermittlung der optimalen Fertigungslosgröße bei der Sorten- und der Serienfertigung besondere Bedeutung. Hierbei werden mehrere produktions- und häufig auch absatzverwandte Erzeugnisse nacheinander auf derselben Produktionsanlage hergestellt, wobei von den Erzeugnisarten jeweils eine bestimmte Menge gefertigt wird, ohne dass deren Produktion durch die Fertigung anderer Erzeugnisse unterbrochen wird.
Um einen vollständigen Produktionsplan zu erhalten, ist neben den Losgrößen die zeitliche Abfolge der Loserstellung verschiedener Erzeugnisarten festzulegen. Dabei ist zu beachten, dass die Bedarfsanforderungen befriedigt werden und sich überschneidungsfreie Maschinenbelegungspläne ergeben. Neben diesem Lossequenzproblem ergibt sich ein Reihenfolgeproblem, sobald der Rüstaufwand für Aufträge von der Reihenfolge ihrer Bearbeitung abhängt (Adam, D. 2001).
Liegen Engpässe im Fertigungsbereich vor, sodass in der Planungsperiode nicht alle Erzeugnisarten in Höhe der jeweiligen Absatzhöchstmenge hergestellt werden können (alternative Fertigung), so sind die optimalen Losgrößen simultan mit dem Produktionsprogramm zu planen. Ursache für diese Interdependenz ist die Abhängigkeit der auftretenden Kosten sowie der verfügbaren Produktionszeiten und damit der Erlöse von der Höhe der Losgrößen (Adam, D. 1990). Im Folgenden werden einige statische deterministische Modelle betrachtet, die Konstanz der Parameter im Zeitablauf voraussetzen und die existierende Unsicherheit vernachlässigen.
II. Entscheidungsrelevante Kosten bei der Losgrößenbestimmung
Die Bestimmung optimaler oder wirtschaftlicher Losgrößen muss sich an der Zielsetzung des Unternehmens ausrichten. So resultieren aus dem Ziel der Gewinnmaximierung deutlich höhere Losgrößen als bei Maximierung der Rentabilität des gebundenen Kapitals (Pack, L. 1989). Wird – wie im Folgenden – die Maximierung des Gewinns angestrebt, so reduziert sich das wirtschaftliche Ziel bei der Bestimmung von Losgrößen auf die Minimierung der durch die Losgrößenentscheidung anfallenden Kosten, sofern die Erlöse von der Höhe der Losgrößen und der zeitlichen Verteilung der Produktion unabhängig sind.
Im Rahmen der hier beschriebenen, kurzfristig orientierten, operativen Losgrößenplanung sind nur solche Kostenarten entscheidungsrelevant, bei denen sich die anfallenden periodenbezogenen Kosten durch die Höhe der Losgröße und die zeitliche Verteilung der Loserstellung verändern lassen. Nicht relevant für die operative Losgrößenplanung sind dann Kosten, die durch die Bereitstellung von Kapazitäten anfallen.
Kosten, die unabhängig von der Höhe der Losgröße bei jedem gefertigten oder beschafften Los anfallen, werden als losfixe Kosten bezeichnet. Im Bereich der Fertigung ist bei Sorten- und Serienfertigung davon auszugehen, dass mit jeder Umstellung der betreffenden Produktionsanlage von der Bearbeitung einer Erzeugnisart auf eine andere die Anlage umgerüstet bzw. eingerichtet wird. Neben den durch auftretenden Faktorverzehr anfallenden direkten Rüstkosten entstehen indirekte Rüstkosten, falls die betrachtete Produktionseinheit einen Engpass darstellt und damit die verfügbare Produktionszeit durch die Rüstzeiten gewinnmindernd reduziert wird. Zusätzlich zu den Rüstkosten i.e.S. entstehen häufig Anlaufkosten aufgrund einer geringeren Produktivität während der Anlaufphase des neuen Produktionsloses. Diese losfixen Kosten wirken damit in Richtung auf möglichst wenige Losauflagen je Erzeugnisart.
Eine entgegengesetzte Wirkung haben die Kosten der Lagerhaltung, deren Hauptbestandteil die Kapitalbindungskosten darstellen. Diese ergeben sich mittels Multiplikation der im Zeitablauf auftretenden wertmäßigen Lagerbestände mit dem planungszeitraumbezogenen Kalkulationszinssatz. Werden Aufwendungen für die Handhabung, Pflege und Versicherung der gelagerten Güter erforderlich, so sind die hiermit verbundenen Kosten immer dann im Rahmen einer operativen Planung entscheidungsrelevant, wenn sie direkt mit der Höhe der Losgröße variieren. Eine Minimierung von Lagerhaltungskosten wird damit bei einer möglichst großen Anzahl Lose bzw. einer geringstmöglichen Losgröße erreicht; dies würde einer vollständigen Anpassung (Synchronisation) der Versorgungsströme an den Bedarf im Zeitablauf entsprechen.
Die Kosten des zu beschaffenden Materials im Falle der Beschaffungslosgrößenplanung sowie die Kosten der Bearbeitung der Erzeugnisse im Falle der Produktionslosgrößenplanung sind so lange nicht entscheidungsrelevant, wie diese sich nicht mit der Höhe der Losgröße ändern.
III. Das Grundmodell der Losgrößenplanung
Das von Harris (Harris, F. 1913) eingeführte Grundmodell der Losgrößenplanung ist identisch für die Fertigungs- und Beschaffungslosgrößenplanung. Folgende Modellprämissen sind zu beachten:
| - | Es wird nur genau ein Lager für eine Erzeugnisart betrachtet, das sich hinter einer Fertigungsstufe, auf der die betrachtete Produktart hergestellt wird, befindet bzw. welches das Wareneingangslager darstellt (einstufiges Einproduktartenmodell). | | - | Die Bedarfsrate ist im Zeitablauf konstant, der Lagerabgang erfolgt kontinuierlich. | | - | Die Lagerauffüllzeit ist null, d.h. gelieferte Beschaffungsmengen stehen mit dem Lieferzeitpunkt sofort zum Verbrauch bereit bzw. die Produktion des Loses erfolgt ohne Zeitverzug. | | - | Alle planungsrelevanten Daten sind bekannt und nicht mit Unsicherheit behaftet (deterministisches Modell). | | - | Beschränkungen hinsichtlich der Losgröße oder der Anzahl Lose im Planungszeitraum werden nicht wirksam. Die Losauflagezeitpunkte sind beliebig wählbar. | | - | Eine geplante Herbeiführung von Bedarfsunterdeckungen (Fehlmengen) ist unzulässig. |
Zur mathematischen Formulierung des Modells werden die folgenden Variablen eingeführt:
| - | kR: losfixe Kosten in Geldeinheiten [GE] je Bestell- bzw. Rüstvorgang | | - | kL: Lagerkostensatz in [GE] je Mengeneinheit [ME] und Zeiteinheit [ZE] | | - | z: Zinssatz je [ZE] zur Ermittlung der Kapitalbindungskosten | | - | w: Wert je gelagerter [ME] | | - | b: Bedarfsrate je [ZE] | | - | T: Länge des Planungszeitraums in [ZE] | | - | x: Losgröße | | - | n: Losauflagehäufigkeit im Planungszeitraum (vgl. Abb. 1) |
Die gesamten losfixen Kosten in Abhängigkeit von der Losauflagehäufigkeit betragen im Planungszeitraum:
KR(n) = kR · n (1)
Soll die optimale Losgröße ermittelt werden, so ist diese Funktion in Abhängigkeit von x auszudrücken. Da der Gesamtbedarf im Planungszeitraum durch das Auflegen/Beschaffen von n Losen gedeckt wird, ergibt sich:

Durch Substitution von n in (1) erhält man:
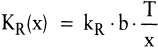 (2) (2)
Aufgrund des unterstellten kontinuierlichen Lagerabgangs in Höhe der Bedarfsrate b ergibt sich eine lineare Lagerbestandsfunktion. Zu jedem Lieferzeitpunkt erfolgt eine Auffüllung des soeben auf einen Bestand von null gesunkenen Lagerbestands bis auf die maximale Lagermenge, die exakt der Losgröße entspricht. Somit kann der Lagerbestand im Zeitablauf auf einfache Weise bestimmt werden: Er entspricht im Durchschnitt der Hälfte des maximalen Lagerbestands. Die Funktion der Lagerhaltungskosten in Abhängigkeit von der Losgröße lautet:
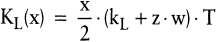 (3) (3)
Die zu minimierende Zielfunktion der Gesamtkosten setzt sich aus (2) und (3) zusammen:
K(x) = KL(x) + KR(x) ⇒ min! (4)
Als notwendige Bedingung für ein Minimum ergibt sich:
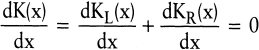 (5) (5)
Hieraus kann die Aussage abgeleitet werden, dass sich die Steigungen der Funktionen der losfixen Kosten und der Lagerhaltungskosten im Optimum betragsmäßig entsprechen müssen:
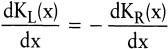 (6a) (6a)
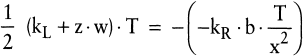 (6b) (6b)
Werden ausschließlich entscheidungsrelevante Kosten in die Zielfunktion aufgenommen, so liegt im Optimum auch Gleichheit von Lagerhaltungskosten und losfixen Kosten vor, wie durch Multiplikation von (6b) mit der Losgrößenvariable x nachvollzogen werden kann.
Durch Umformung von (6b) kann die optimale Losgrößenformel entwickelt werden:
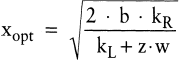 (7) (7)
Die hinreichende Bedingung für ein Minimum ist erfüllt, da alle Größen in dieser Bedingung nicht negativ sein müssen:
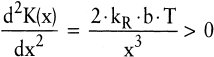 (8) (8)
Es wird deutlich, dass die optimale Losgröße ohne Kenntnis der Länge des Planungszeitraums ermittelt werden kann. Übersteigt jedoch xopt den Wert b · T, so wäre der Gesamtbedarf im Planungszeitraum die optimale Losgröße. Unter praktischen Gegebenheiten ist bei der Umsetzung einer in dieser Weise ermittelten Losgröße zu beachten, dass sich sowohl für die Losgröße als auch für die Anzahl der Lose im Planungszeitraum nicht ganzzahlige Größen ergeben können. Insofern wäre die Losgröße auf eine liefer- bzw. produzierbare Anzahl Mengeneinheiten festzulegen, wobei für die beiden direkt benachbarten ganzzahligen Werte ein Kostenvergleich durchzuführen wäre. Dabei kann ein Aufrunden der Losgröße aufgrund des flacheren Zielfunktionsverlaufs für zunehmende Stückzahlen auch dann vorteilhaft sein, wenn das ermittelte xopt näher an der benachbarten, kleineren ganzzahligen Losgröße liegt. Ein entsprechender Kostenvergleich ist auch für die beiden benachbarten ganzzahligen Losauflagehäufigkeiten durchzuführen, sofern nicht angenommen werden kann, dass die Parameter auch für folgende Planungszeiträume Gültigkeit besitzen und der Planungszeitraum theoretisch als unendlich angenommen werden kann.
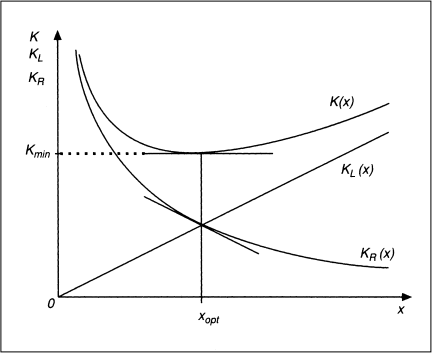
Abb. 1: Typischer Kostenfunktionsverlauf beim statischen Losgrößenmodell
IV. Einstufige Losgrößenmodelle mit endlicher Lagerauffüllgeschwindigkeit
Die Annahme einer unendlichen Lagerauffüllgeschwindigkeit ist nur dann haltbar, wenn die für die Auffüllung des Lagers erforderliche Zeit in Relation zur Verbrauchszeit eines Loses vernachlässigbar gering ist. Während dies für die Beschaffungslosgrößenplanung in vielen Fällen gerechtfertigt erscheint, dürfte diese Situation für die Planung der Fertigungslosgröße eher eine Ausnahme darstellen. Im Folgenden sei angenommen, dass auf einer Produktionsanlage je [ZE] xp [ME] einer betrachteten Erzeugnisart gefertigt werden können und die Lagerentnahmerate dieser Erzeugnisart xv [ME/ZE] beträgt. Des Weiteren soll davon ausgegangen werden, dass eine offene Produktion vorliegt, d.h. erzeugte Güter sofort dem Lager zwecks Verkauf oder Weiterverarbeitung entnommen werden können. Für xp > xv wird die vorübergehende Einstellung der Fertigung der betrachteten Produktart auf der Anlage erforderlich, um den Lagerbestand nicht zu stark anwachsen zu lassen. Diesen, als Staulager bezeichneten, Fall zeigt Abb. 2.
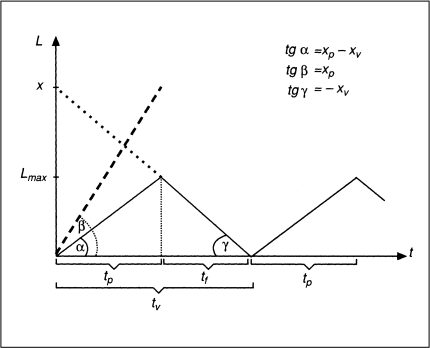
Abb. 2: Staulager bei offener Produktion
Während der Produktionsdauer tp des Loses erfolgt bereits ein Lagerabbau, wobei zwecks einfacherer Formulierung des Problems unterstellt wird, dass eine Lagerentnahme bereits erfolgen kann, während die erste Einheit noch produziert wird. Die Losmenge x wird innerhalb von tv [ZE] verbraucht, womit für die betrachtete Anlage eine verfügbare Restzeit – innerhalb derer u.a. andere Sorten gefertigt werden können – von tf = tv – tp [ZE] verbleibt. Der durchschnittliche Lagerbestand entspricht der Hälfte des maximalen Bestandes Lmax, der u.a. mittels der Beziehung tp · (xp – xv) ermittelt werden kann. Da tp · xp = x und damit tp = x/xp gilt, kann der durchschnittliche Lagerbestand Ld beschrieben werden durch:
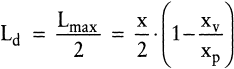 (9) (9)
Der Gesamtbedarf B im Planungszeitraum T entspricht xv · T. Bei verkürzter Schreibweise mit cL = (kL + z · w) sind die zu minimierenden entscheidungsrelevanten Kosten:
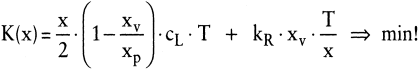
(10)
Nach Differentiation und Nullsetzen der ersten Ableitung sowie Umformung ergibt sich die Losgrößenformel für den Fall eines Staulagers mit offener Produktion:
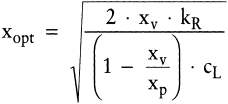 (11) (11)
Mit Kenntnis der optimalen Losgröße xopt können die weiteren interessierenden Größen bestimmt werden:
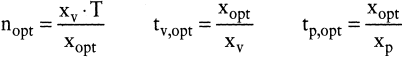
Alternativ kann die Zielfunktion in Abhängigkeit einer dieser Größen formuliert und die optimale Losgröße so indirekt bestimmt werden. Die optimale verfügbare Restzeit der Fertigungsstufe vor dem betrachteten Lager beträgt tf,opt = tv,opt – tp,opt; die Folgestufe arbeitet bzw. der Absatz erfolgt permanent.
Ist entgegen der bisherigen Annahme die Lagerentnahmerate größer als die Produktionsrate (xv > xp), so müsste die betrachtete Produktionsstufe permanent arbeiten, um die jeweils unterbrechungsfreie Einstellung der einzelnen Lose auf der Folgestufe zu ermöglichen. Vor Auflegen eines Loses auf der Folgestufe müsste also bereits ein gewisser Lagerbestand gefertigt worden sein. Diese als Zerreißlager bezeichnete Situation ist in Abb. 3 skizziert, wobei tf hier die verfügbare Restzeit der Folgestufe angibt.
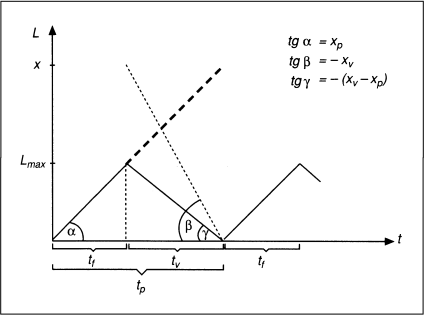
Abb. 3: Zerreißlager bei offener Produktion
Der durchschnittliche Lagerbestand ergibt sich in diesem Fall u.a. über die Beziehung:
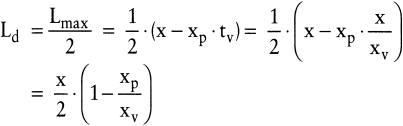
(12)
Wie ein Vergleich von (12) und (9) zeigt, unterscheiden sich der durchschnittliche Lagerbestand und damit die Lagerhaltungskostenfunktion von Zerreiß- und Staulagerfall lediglich darin, dass im Multiplikator für die Losgröße x im Quotienten eine Vertauschung von Zähler und Nenner stattgefunden hat, sodass die kleinere Geschwindigkeit – hier xp, vorher xv – im Zähler steht. Da die Rüstkosten gegenüber dem Staulagerfall unverändert bleiben, ergibt sich als optimale Losgrößenformel:
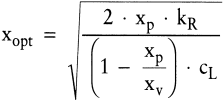 (13) (13)
Offensichtlich unterscheiden sich (11) und (13) lediglich dadurch, dass die Variablen xp und xv jeweils gegeneinander ausgetauscht sind. Durch Erweitern von (11) mit 1/xv und (13) mit 1/xp wird deutlich, dass eine gemeinsame Formel für die optimale Losgröße bei offener Produktion im Stau- und im Zerreißlagerfall verwendet werden kann:
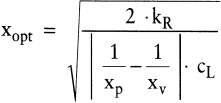 (14) (14)
Ist ein Los auf einer betrachteten Produktionsstufe erst vollständig fertig zu stellen, bevor es abgesetzt oder weiterverarbeitet werden kann (geschlossene Fertigung), so wird zunächst während der Produktionszeit tp das gesamte Los produziert, sodass sich ein maximaler Lagerbestand in Höhe von x ergibt, unabhängig davon, ob es sich um ein Stau- oder Zerreißlager handelt. Anschließend wird das Los während der Verbrauchszeit tv vollständig dem Lager entnommen. Die Liegezeit des durchschnittlichen Lagerbestandes Lmax/2 = x/2 beträgt somit – unabhängig vom Lagertyp – je Los tp + tv = x/xp + x/xv. Die Anzahl Lose im Planungszeitraum ist n = B/x, sodass die Kostenfunktion lautet:
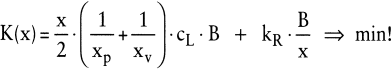
(15)
Die hieraus abzuleitende Formel für die optimale Losgröße bei geschlossener Fertigung lautet:
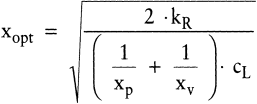 (16) (16)
V. Mehrstufige Modelle
Für mehrstufige Produktionsprozesse ist die isoliert für einzelne Fertigungsstufen vorgenommene Ermittlung von Losgrößen im Rahmen der Modellannahmen nicht sinnvoll, da unterschiedliche Losgrößen lediglich zusätzliche Lagerbestände vor solchen Stufen verursachen, für die vergleichsweise geringere Losgrößen bestimmt wurden. Bei der Bestimmung einer gemeinsamen, für alle Produktionsstufen geltenden Losgröße für eine betrachtete Erzeugnisart ist zu berücksichtigen, dass in Fertigungsstufen, die schneller als die langsamste Stufe arbeiten bzw. die mit einer größeren Geschwindigkeit als der Absatzrate produzieren, bei optimaler Fertigung zeitweise keine Zwischenlagerbestände vorhanden sind. Abb. 4 verdeutlicht diese Situation anhand des Beispiels einer zweistufigen Fertigung mit Zwischenprodukt-Zerreißlager und Fertigprodukt-Staulager.
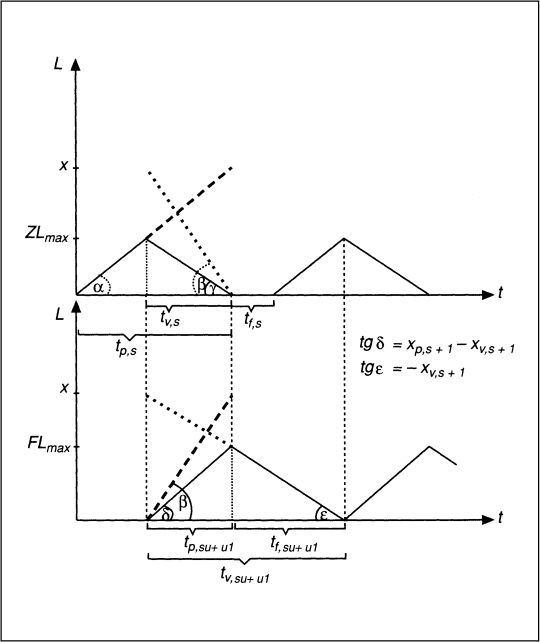
Abb. 4: Zweistufige Fertigung mit Zwischenprodukt-Zerreißlager und Fertigprodukt-Staulager
Aufgrund der Tatsache, dass u.U. in den Lagern der Fertigungsstufen zeitweise keine Bestände an einer Erzeugnisart vorhanden sind, kann der durchschnittliche Lagerbestand eines Loses nicht als repräsentativ für den Gesamtplanungszeitraum angenommen werden. Stattdessen ist der Durchschnittsbestand je Los mit der Anzahl Lose im Planungszeitraum zu multiplizieren. Die Stufenleistungen der S Stufen seien im Folgenden mit xp,s und die Absatzrate mit xp,S+1 bezeichnet. Die Rüstkosten je Stufe kR,s sind zu beachten sowie der stufenbezogene Lagerhaltungskostensatz cL,s. Für das Beispiel der Abb. 4 lautet dann die Funktion der losweisen Lagerhaltungskosten LKs im Zwischenlager (s = 1):
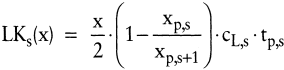 (17) (17)
Die Lagerhaltungskostenfunktion KL,s im Planungszeitraum für dieses Lager ergibt sich nach Multiplikation von LKs mit der Auflagehäufigkeit n = B/x. Nach Ersetzen von tp,s durch x/xp,s und anschließendem Vereinfachen ergibt sich:
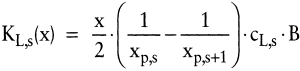 (18) (18)
Für S Fertigungsstufen, einschließlich der Endproduktstufe, sind die Lagerhaltungs- und Rüstkosten zu minimieren, wobei für synchronisierte Fertigungsstufen keine Lagerbestände und damit keine Lagerhaltungskosten anfallen, wohingegen die Rüstkosten aller Stufen zu berücksichtigen sind. Da sowohl Stau- als auch Zerreißlager auftreten können, ist jeweils der Betrag der Differenzen aus den Kehrwerten der Stufenleistungen anzusetzen:
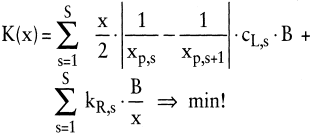
(19)
Wie aus (14) und (16) zu ersehen ist, kann für die beiden Lager- und Produktionstypen die folgende, gemeinsame Formel zur Ermittlung der optimalen Losgröße einer Erzeugnisart bei mehrstufiger Fertigung angegeben werden:
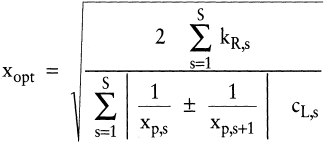 (20) (20)
VI. Simultanplanung von Losmenge und Lossequenz
Stellt eine Unternehmung mehrere Produktarten her, so ist in der Durchführungsplanung sicherzustellen, dass zulässige Belegungspläne für die Fertigungseinrichtungen vorliegen. Da bei einer für jede Erzeugnisart isolierten Losgrößenplanung überschneidungsfreie Belegungspläne nur zufällig entstehen, wären die Losgrößen und die Reihenfolge der Losbearbeitung auf den Anlagen simultan zu planen. Dieses komplexe Problem kann bei Betrachtung nur einer Stufe sowie bei Unterstellen von Rüstzeiten bzw. -kosten, die unabhängig von der Losreihenfolge sind, auf die folgende Weise einer Lösung näher gebracht werden.
Die Zulässigkeit eines Belegungsplanes für eine Anlage kann gewährleistet werden, wenn die Gesamtkapazität der betrachteten Stufe unter Berücksichtigung der Rüstzeiten für die Bearbeitung aller Aufträge ausreichend ist und die Losauflagehäufigkeit für alle Sorten identisch ist (Adam, D. 1965; Adam, D. 1990). Kostengünstigere, aber nicht zwangsläufig zulässige Lösungen können sich ergeben, wenn die Auflagehäufigkeit einer Sorte ein ganzzahliges Vielfaches einer anderen Sorte betragen soll. Neben der zu minimierenden Zielfunktion, die die Kosten aller Erzeugnisarten summiert, treten dann Nebenbedingungen der Art:
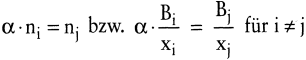
Dieses Problem kann mittels der Lagrangeschen Multiplikatorenmethode einer Lösung zugeführt werden. Ein vereinfachter Ansatz ergibt sich, sofern gefordert wird, dass die Lose aller I Erzeugnisarten gleich häufig aufzulegen sind (vgl. Adam, D. 1990); Bloech, J. et al. 2004). In diesem Fall kann die Zielfunktion über die für alle Produktarten gemeinsame Auflagehäufigkeit n definiert werden, wobei hier ein Staulager mit offener Produktion unterstellt wurde:
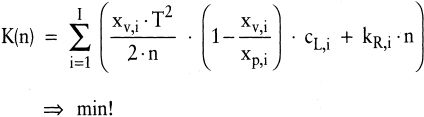
(21)
Die notwendige Bedingung für ein Minimum lautet:
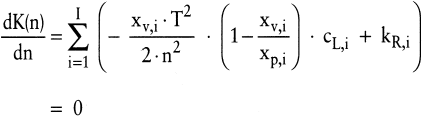
(22)
Als – im Rahmen dieser Problemformulierung – optimale Losauflagehäufigkeit für alle Produktarten ergibt sich:
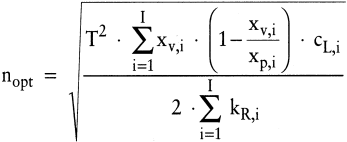 (23) (23)
Damit lauten die »optimalen« Losgrößen
xi.opt = Bi/nopt für i = 1, ?, I.
Dieser Ansatz lässt sich für den Fall abwandeln, dass eine Losgrößenplanung für Teilefamilien durchgeführt werden soll (Adam, D. 2001). Dabei fallen für eine Anzahl M an Produktarten, die unter fertigungstechnischen Aspekten zu einer Teilefamilie zusammengefasst wurden und die beispielsweise mittels flexibler Fertigungstechniken unter Einsatz eines automatischen Werkzeugmagazins hergestellt werden können, für die Auflage einer nahezu beliebigen – lediglich durch technische und organisatorische Restriktionen eingeschränkten – Anzahl Lose der Teilefamilie lediglich einmalig Rüstkosten an. Wird vorausgesetzt, dass jede Produktart innerhalb einer Teilefamilie gleich häufig aufgelegt werden soll, so lautet die Kostenfunktion Kt für die Teilefamilie t in Abhängigkeit von der Auflagehäufigkeit nt im Falle eines Staulagers bei offener Produktion:
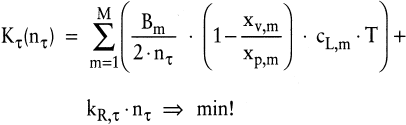
(24)
Als optimale Auflagehäufigkeit der Teilefamilie ergibt sich unter den gemachten Annahmen:
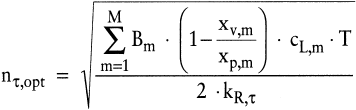 (25) (25)
Existieren mehrere Möglichkeiten zur Bildung von Teilefamilien, so ist diese Entscheidung unter Beachtung der anfallenden Kosten zu fällen, die von den sich ergebenden Losgrößen für die Produktarten der Teilefamilien abhängen.
VII. Kapazitätsbeschränkungen in Losgrößenmodellen
In der betrieblichen Realität sind aufgrund beschränkter Kapazitäten Restriktionen bei der Planung der Losgrößen der einzelnen Erzeugnisarten zu berücksichtigen. Diese können sich zum einen auf die Fertigungskapazität beziehen, zum anderen können Beschränkungen hinsichtlich logistischer sowie finanzieller Kapazitäten auftreten. Im Folgenden wird vom Lossequenzproblem wieder abstrahiert.
1. Lagerrestriktionen im einstufigen Mehrproduktartenmodell
Da die Formulierung von Restriktionen bezüglich verfügbarer Finanzmittel, interner und externer logistischer Handling- und Transportkapazitäten sowie hinsichtlich der Planungskapazitäten (Disposition) im statischen Modellansatz auf nur teilweise zufrieden stellende Weise möglich ist (Bogaschewsky, R. 1989), sollen hier lediglich Beschränkungen der verfügbaren Lagerkapazität aufgegriffen werden.
Benötigt jede gelagerte Mengeneinheit einer Erzeugnisart i für ihre Lagerung ai Raumeinheiten [RE] und stehen im Planungszeitraum jederzeit LKap [RE] zur Verfügung, so kann die Lagerrestriktion im Falle eines Staulagers bei offener Produktion wie folgt formuliert werden:
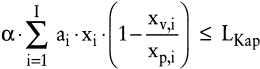 (26) (26)
Existieren zu Beginn des Planungszeitraums keine Lagerbestände für die I Produktarten, so wäre durch Einstellen von a = 1 sicherzustellen, dass alle – in diesem Fall auf unterschiedlichen Anlagen parallel zu fertigenden – Produktarten gelagert werden können. Da bei einer Sorten- oder Serienfertigung die Lose nacheinander hergestellt werden, kann a kleiner gewählt werden, wobei zu geringe Werte für a zu Kapazitätsverletzungen führen können, während zu große Werte tendenziell dazu führen, dass die verfügbare Kapazität nicht ausgelastet wird. Reicht die Kapazität für die optimalen Losgrößen ohne Berücksichtigung der Lagerrestriktion nicht aus, so kann das Optimierungsproblem unter Berücksichtigung der Lagerkapazitätsrestriktion als Lagrange-Ansatz – mit XT = (x1, x2, ?, xI) – wie folgt formuliert werden:
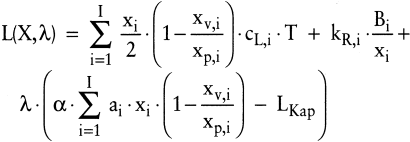
(27)
Wird die partielle Ableitung nach dem Lagrangeschen Multiplikator λ gleich null gesetzt, ergibt sich die Lagerbeschränkung als Gleichheitsrestriktion. Diese Formulierungsweise ist nur dann korrekt, wenn das unbeschränkte Optimum die Lagerrestriktion verletzt. Die partiellen Ableitungen nach den Losgrößenvariablen xi lauten:
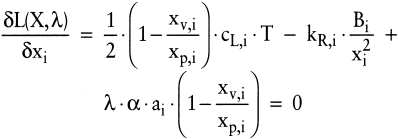
(28)
Als im Rahmen dieses Modellansatzes optimale restringierte Losgrößen ergeben sich:
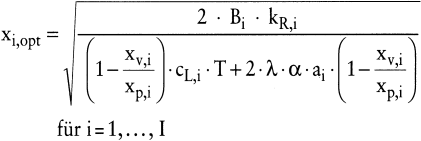
(29)
2. Beschränkte Fertigungskapazität im einstufigen Mehrproduktartenmodell
Wird die Fertigungskapazität FKap in [ZE] bezogen auf den Planungszeitraum T gemessen, so stellt diese einen Engpass dar, sobald die Summe der reinen Bearbeitungszeiten TB,i auf einer betrachteten Anlage für die – durch die Programmplanung vorab determinierten – Gesamtbedarfe der Erzeugnisarten i zuzüglich der anfallenden Rüstzeiten TR,i größer ist als Fkap. Somit kann die folgende Nebenbedingung für die Losgrößenbestimmung formuliert werden:
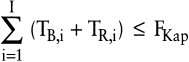 (30) (30)
Da die Summe der reinen Bearbeitungszeiten im Rahmen der Losgrößenplanung nicht zur Disposition steht, ist für den Fall, dass die Fertigungskapazität zur Herstellung der optimalen Losgrößen nicht ausreicht, die Summe der Rüstzeiten derart zu reduzieren und damit die Losgrößen zu erhöhen, dass die Fertigungskapazität eingehalten wird. Bei Bezeichnung der hier als reihenfolgeunabhängig angenommenen Rüstzeit je Losauflage für die Produktart i mit tR,i ergibt sich die gesamte Rüstzeit für eine Erzeugnisart aus:
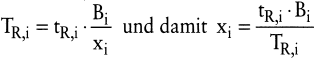
Die zu minimierenden erzeugnisspezifischen Kostenfunktionen in Abhängigkeit von den Rüstzeiten im Planungszeitraum lauten für ein Staulager bei offener Produktion (Adam, D. 1990, Adam, D. 2001):
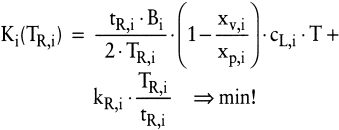
(31)
Als notwendige Bedingung für das Kostenminimum ergibt sich:
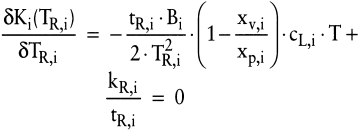
(32)
Unter Ausnutzen der Beziehungen
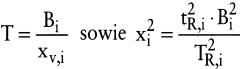
kann geschrieben werden:
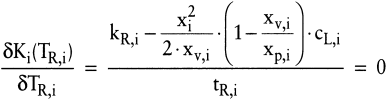 (33) (33)
Dieser Ausdruck entspricht der Differenz von erzeugnisspezifischen Rüst- und Lagerhaltungskosten je Los bezogen auf die losweise Rüstdauer. Im beschränkten Optimum entsprechen sich die Grenzkosten für alle Erzeugnisarten, und die Nebenbedingung ist exakt einzuhalten. Damit ist das folgende Gleichungssystem zu lösen:
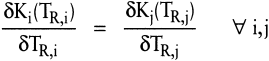
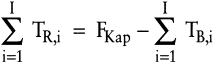
VIII. Reduzierung der Losgrößen durch Rüstkostensenkung
Das Ziel der Losgröße \'1\' bzw. die extreme Reduzierung der Lagerhaltungskosten lässt sich nur dann unter Wirtschaftlichkeitsgesichtspunkten realisieren, wenn die Rüstkosten entsprechend niedrig sind. Ein solcher Ansatz wurde in der Automobilindustrie erstmals von der Toyota Motor Corporation umgesetzt, die in ihren Werken die Umrüstzeiten extrem reduzieren konnte (vgl. Shingo, S. 1993). Damit wurden die Voraussetzungen für eine nahezu bedarfssynchrone Fertigung – mit sehr geringen Losgrößen, die wiederum kurze Durchlaufzeiten, eine vergleichsweise hohe Flexibilität und niedrige Kapitalbindungskosten bedingen – geschaffen. Dies ermöglichte die Installation eines dezentralen, aus selbststeuernden Regelkreisen bestehenden Fertigungssteuerungssystems, das gemäß dem über Karten stattfindenden Informationsaustausch als Kanban-System bezeichnet wurde.
Ist die Reduzierung der Rüstzeiten bzw. der Rüstkosten mit zusätzlichen Kosten verbunden, so wären diese im Rahmen einer – nicht mehr rein operativen – Planung in den Entscheidungsansatz einzubeziehen. Wie bei der Ausgestaltung der Fertigungseinrichtungen oder der logistischen Kapazitäten, werden durch die in diesem Zusammenhang zu treffenden Entscheidungen Rahmenbedingungen für die operative Losgrößenplanung gesetzt. Dies erfordert eine Vorgehensweise, die möglichst alle Folgewirkungen dieser Entscheidungen in Betracht zieht und die daher nicht ohne weiteres auf die reine Losgrößenplanung reduziert werden kann. Einen Ansatz, wie die Berücksichtigung des Kapitaldienstes einer rüstkostensenkend wirkenden Investition im Rahmen der Losgrößenplanung erfolgen kann, zeigt Adam (Adam, D. 1990, Adam, D. 2001).
Literatur:
Adam, D. : Produktionsplanung bei Sortenfertigung, Hamburg 1965
Adam, D. : Produktionsdurchführungsplanung, in: Industriebetriebslehre, hrsg. v. Jacob, H., 4. A., Wiesbaden 1990, S. 673 – 918
Adam, D. : Produktionsmanagement, 9. A., Wiesbaden 2001
Alscher, J. : Mehrprodukt-Lagerhaltung mit Standard-Lagerhaltungsmodellen, Rheinfelden 1986
Axsäter, S. : Evaluation of Lot-Sizing Techniques, in: IJProdRes, 1986, S. 51 – 57
Bloech, J. : Einführung in die Produktion, 5. A., Berlin et al. 2004
Bogaschewsky, R. : Dynamische Materialdisposition im Beschaffungsbereich, Frankfurt a.M. 1988
Bogaschewsky, R. : Statische Materialdisposition im Beschaffungsbereich, in: WiSt, 1989, S. 542 – 548
Brink, A. : Operative Lager- und Bestellmengenplanung unter besonderer Berücksichtigung von Lagerkapazitätsrestriktionen, Bergisch Gladbach 1988
Churchman, C. W./Ackoff, R. L./Arnoff, E. L. : Operations Research, Wien 1961
Gupta, Y./Keung, Y. K. : A Review of Multi-Stage Lot-Sizing Models, in: IJOPM, 1990, S. 57 – 73
Gupta, Y. P./Keung, Y. K./Gupta, M. C. : Comparative Analysis of Lot-Sizing Models for Multi-Stage Systems: a Simulation Study, in: IJProdRes, 1992, S. 695 – 716
Gutenberg, E. : Grundlagen der Betriebswirtschaftslehre, Bd. I: Die Produktion, 24. A., Berlin et al. 1983
Hadley, G./Whitin, T. M. : Analysis of Inventory Systems, Englewood Cliffs 1963
Harris, F. : How Many Parts to Make at Once, in: Factory – The Magazine of Management, 1913, S. 135 – 136
Hechtfischer, R. : Kapazitätsorientierte Verfahren der Losgrößenplanung, Wiesbaden 1991
Heinricht, C. E. : Mehrstufige Losgrößenplanung in hierarchisch strukturierten Produktionsplanungssystemen, Berlin/Heidelberg 1987
Kurbel, K. : Simultane Produktionsplanung bei mehrstufiger Serienfertigung, Berlin 1978
Majerus, M. : Produktions- und Investitionsplanung bei flexibler Automatisierung, Bergisch Gladbach, Köln 1989
Müller-Merbach, H. : Die Bestimmung optimaler Losgrößen bei Mehrproduktfertigung, Darmstadt 1962
Pack, L. : Gewinnmaximale oder rentabilitätsmaximale Losgröße bzw. Bestellmenge?, in: ZfB, 1989, S. 5 – 26
Schneeweiß, C. : Modellierung industrieller Lagerhaltungssysteme, Berlin et al. 1981
Shingo, S. : Das Erfolgsgeheimnis der Toyota Produktion, 2. A., Landsberg a.L. 1993
Stadtler, H. : Hierarchische Produktionsplanung bei losweiser Fertigung, Heidelberg 1988
Tempelmeier, H. : Material-Logistik, 6. A., Berlin et al. 2006
Zwehl, W. v. : Kostentheoretische Analyse des Modells der optimalen Bestellmenge, Wiesbaden 1973
|