|
Optionsbewertungsmodelle
Inhaltsübersicht
I. Vorbemerkung
II. Modellunabhängige Wertgrenzen
III. Duplikationsmodelle
IV. Gleichgewichts- und sonstige Modelle
V. Empirische Überprüfung
I. Vorbemerkung
Optionen verbriefen für den Käufer das Recht, nicht aber die Pflicht, eine bestimmte Anzahl von Finanztiteln oder Waren (Basisinstrumente) innerhalb einer bestimmten Frist zu einem heute festgesetzten Preis zu kaufen oder zu verkaufen. Beim Kaufrecht spricht man von einem Call, beim Verkaufsrecht von einem Put. Der jeweils zu leistende Geldbetrag für eine Einheit des Basisinstruments heißt Basispreis. Ist die Ausübung des Optionsrechtes nur am Verfalltag möglich, spricht man von einer europäischen Option; kann die Option jederzeit bis zum Verfalltag ausgeübt werden, liegt eine Option vom amerikanischen Typ vor. Optionsbewertungsmodelle (OBM) dienen in erster Linie der Bestimmung des fairen Preises von börsengehandelten Optionen, und im Falle seiner Abweichung vom Marktpreis, dem Aufbau profitabler Arbitragepositionen. Daneben werden OBM z.B. zur Bewertung von (noch) nicht börsengehandelten Finanztiteln mit Optionscharakter, zur anreizkompatiblen Kontraktgestaltung und zur Bewertung der in Realinvestitionen innewohnenden Flexibilität herangezogen (Mason, S./Merton, R.C. 1985).
Am Verfalltag einer Option ergibt sich ihr Wert unmittelbar aus dem zugrundeliegenden Kontrakt. Er entspricht ihrem Ausübungswert und ist im Falle eines Calls auf eine Aktie gleich der Differenz zwischen dem Kurs der zugrundeliegenden Aktie und dem kontrahierten Basispreis, sofern diese Differenz nicht negativ ist. Wie aber ist der Gegenwartswert einer Option vor ihrem Verfalltag einzuschätzen? Eine erste Antwort dazu liefert die frühe Arbeit von Bachelier (Bachelier, L. 1900), in der unter Vernachlässigung der Risikoaversion von Investoren eine erste Bewertungsformel vorgestellt wird, die eine (arithmetische) Brownsche Bewegung der Aktienkurse unterstellt. Letztere Modellannahme impliziert normalverteilte Aktienkurse, d.h. es werden modellmäßig auch negative Aktienkurse zugelassen. Trotz dieser theoretischen Mängel dauert es mehr als 60 Jahre bis eine zweite Modellgeneration vorgestellt wird, die von logarithmisch normalverteilten Aktienkursen ausgeht (Sprenkle, C.M. 1961; Boness, A.J. 1964; Samuelson, P.A. 1965; Samuelson, P.A./Merton, R.C. 1969). Diese Modellgeneration besitzt allerdings noch den Nachteil, dass die resultierenden Optionswerte von ad hoc spezifizierten Risikopräferenzparametern abhängen.
Eine theoretisch elegante und praktikable Antwort liefert dagegen die von Black, Scholes und Merton (Black, /Scholes, 1973; Merton, 1973) begründete Theorie der Optionsbewertung. Das Bahnbrechende in den Arbeiten von Black/Scholes und Merton besteht darin, zu zeigen, dass ein aus Optionen und zugrundeliegenden Aktien bestehendes Portefeuille zeitstetig derart angepasst werden kann, dass sein Ertrag risikolos wird. Die nahezu perfekte Korrelation zwischen der Preisentwicklung für Aktie und Call bietet eine intuitive Erklärung für dieses Ergebnis. Die Forderung, dass auf arbitragefreien Märkten die Verzinsung dieses dynamisch angepassten Portefeuilles mit der einer risikolosen Anlage übereinstimmen muss, führt zur klassischen Black/Scholes-Formel für Calls vom europäischen Typ. Das hinter dieser Formel stehende präferenzfreie Bewertungsprinzip wird auch als Arbitrageprinzip oder Duplikationsprinzip bezeichnet (siehe Trautmann, 2006).
Die wirklichkeitsnahe Modellierung der Preisentwicklung von Basisinstrumenten führt jedoch neuerdings wieder zur Einsicht, dass eine Bewertung auf der Basis des zweifellos eleganten Duplikationsprinzips nicht mehr haltbar ist. Es entstehen wieder von Präferenzparametern abhängige Bewertungsmodelle, die nun aber im Rahmen von Gleichgewichtsmodellen abgeleitet werden. Im Weiteren werden ausschließlich Optionen auf Finanztitel, insbesondere auf Aktien, betrachtet.
II. Modellunabhängige Wertgrenzen
Der Wert einer Option lässt sich gedanklich als Summe von innerem Wert und Zeitwert auffassen. Der innere Wert wird üblicherweise dem Ausübungswert gleichgesetzt und entspricht – sofern sich die Optionsausübung lohnt – der Differenz aus Basispreis und dem jeweils aktuellen Kurs der zugrundeliegenden Aktie. Folglich ist der Wert einer Option am Verfalltag immer gleich dem inneren Wert der Option. Falls am Verfalltermin der Aktienkurs geringer als der Basispreis ist, so lohnt es sich für den Käufer eines Calls nicht, diesen auszuüben, und die Option verfällt. Wenn jedoch der Aktienkurs höher als der Basispreis ist, entspricht der Wert des Calls der Differenz aus Aktienkurs und Basispreis. Bezeichnet CT den Wert des Calls am Verfalltag, ST den Aktienkurs am Verfalltag und K den Basispreis des Calls dann gilt CT = max{0,ST – K}. Entsprechend wird der Inhaber eines Puts sein Verkaufsrecht nur dann ausüben, wenn der Aktienkurs am Verfalltermin kleiner als der Basispreis ist. Bezeichnet PT den Wert des Puts am Verfalltag T, so gilt PT = max{0,K – ST}.
Vor dem Verfalltag einer Aktienoption liegt ihr Preis meistens über ihrem Ausübungswert, d.h. die Option besitzt einen positiven Zeitwert. Dies beobachtet man insbesondere bei Calls, falls während der Restlaufzeit auf die Aktie keine Dividende entfällt. Es wird sich zeigen, dass dieser Zeitwert sowohl von der Einschätzung der zukünftigen Aktienkursentwicklung als auch von den Kapitalbindungskosten abhängt. Im Folgenden werden zunächst Unter- bzw. Obergrenzen für den Zeitwert und damit für den Gesamtwert einer Option angegeben, die von der Modellierung der Kursentwicklung der Aktie unabhängig sind. Bei einer beobachteten Verletzung solcher Wertgrenzen besteht die Möglichkeit, profitable, risikolose Zeitarbitrage zu betreiben, falls Optionen sowie die zugrundeliegende Aktie gleichzeitig gehandelt werden können. Unter profitabler, risikoloser Zeitarbitrage wird dabei der Aufbau einer Portefeuilleposition verstanden, deren Liquidationswert bei beliebiger Aktienkursentwicklung nichtnegativ ist und deren Aufbau mit positiven Zahlungsüberschüssen verbunden ist. Im Folgenden wird sowohl für Calls als auch für Puts eine Wertuntergrenze mit Hilfe so genannter Arbitragetableaus abgeleitet. Es wird der Einfachheit halber unterstellt, dass Transaktionskosten vernachlässigbar sind und während der Restlaufzeit einer Aktienoption auf die zugrundeliegende Aktie keine Dividende entfällt.
1. Eine Wertuntergrenze für Calls auf Aktien
Symbolisiert C den aktuellen Wert des Calls, S den aktuellen Aktienkurs, T die Restlaufzeit (in Jahren) und R – T den Diskontierungsfaktor, dann gilt die folgende Wertuntergrenze für Calls vom europäischen Typ (Merton, 1973):
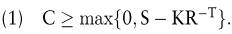
Der Wert eines Calls muss also mindestens der Differenz zwischen gegenwärtigem Aktienkurs und diskontiertem Basispreis entsprechen. Die Handelsstrategie, die von der Verletzung dieser so genannten europäischen Wertuntergrenze profitiert, besteht aus dem Kauf eines Calls, dem Verkauf der zugrundeliegenden Aktie, und der risikolosen Anlage des diskontierten Basispreises. Dieses Portefeuille wird bis zum Verfalltag der Option gehalten und dann liquidiert. Dazu wird die Aktie zum Preis von ST zurückgekauft, um das ursprüngliche Aktienportefeuille wiederherzustellen bzw. eine geliehene Aktie an den Verleiher zurückgeben zu können. Falls sich der Call im Geld befindet, d.h. falls ST > K gilt, wird der Call ausgeübt und erbringt den Nettoerlös ST – K > 0. Andernfalls verfällt der Call wertlos. Die Liquidation der risikofreien Finanzanlage erbringt dagegen in beiden Fällen den Erlös K. Abb. 1 ist nun zu entnehmen, dass neben dem sicheren Arbitragegewinn ε > 0 im Zeitpunkt t = 0, diese Strategie in t = T zudem noch die Zahlung K – ST > 0 verspricht, falls der Aktienkurs den Basispreis nicht übersteigt. 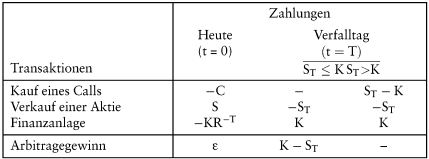
Abb. 1: Profitable Zeitarbitrage bei Verletzung der europäischen Wertuntergrenze
Bei positiven Zinssätzen folgt aus der europäischen Wertuntergrenze, dass sich die Ausübung eines amerikanischen Calls auf eine dividendenlose Aktie vor dem Verfalltag niemals lohnt. Der vor dem Verfalltag erzielbare Marktpreis wird nämlich den aktuellen Ausübungswert S-K, sofern dieser positiv ist, immer übersteigen. Bei einem erwarteten Aktienkursrückgang wird folglich der rational handelnde Besitzer eines Calls den Verkauf des Calls seiner Ausübung vorziehen.
2. Eine Wertuntergrenze für Puts
Die Kombination aus Aktie und europäischem Put mit Basispreis K und Restlaufzeit T besitzt am Verfalltag des Puts das Liquidationswertprofil ST + max (0, K – ST) = max(ST, K). Dasselbe Profil liefert die Kombination eines ansonsten identischen Calls mit einer Finanzanlage mit der Laufzeit T und der Rückzahlung K: max (0, ST – K) + K = max (ST, K). Die Forderung, dass in arbitragefreien Märkten auch die Gegenwartswerte dieser äquivalenten Portefeuilles übereinstimmen müssen, S + P = C + K R – T, führt dann auf die praktisch bedeutsame Put-Call-Parität für Optionen vom europäischen Typ (Stoll, H. 1969):
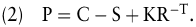
Merton verallgemeinert dieses Ergebnis für Optionen vom amerikanischen Typ, indem er das =-Zeichen durch ein ≥-Zeichen in Beziehung (2) ersetzt:
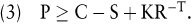
Diese Modifikation kann ökonomisch wie folgt begründet werden. Zum einen sollte, wie bereits festgestellt, ein Call vom amerikanischen Typ nicht vorzeitig (d.h. vor dem Verfalltag) ausgeübt werden. Daher wird der Wert eines Calls vom amerikanischen Typ sich nicht vom Wert eines ansonsten identischen Calls vom europäischen Typ unterscheiden. Andererseits besteht bei Puts vom amerikanischen Typ immer eine positive Wahrscheinlichkeit für die Vorteilhaftigkeit ihrer vorzeitigen Ausübung. Man denke etwa an die Situation eines extremen Kursverfalls der zugrundeliegenden Aktie. Spätestens dann, wenn die Aktie wertlos ist, also der Ausübungswert sein Maximum erreicht hat, sollte der Put ausgeübt werden, um Opportunitätskosten in Form von entgangenen Zinsen auf den Ausübungswert zu vermeiden. Ein Put vom amerikanischen Typ ist also wertvoller als ein ansonsten identischer Put vom europäischen Typ.
III. Duplikationsmodelle
1. Black/Scholes-Modell für Aktienoptionen
Die Festlegung eines absoluten Modell- bzw. Zeitwertes für Aktienoptionen erfordert zusätzliche Annahmen über die zukünftige Aktienkursentwicklung, d.h. über die Wahrscheinlichkeitsverteilung zukünftiger Aktienkurse. Auf der Basis der recht einfachen binomialen Verteilungshypothese soll nun im folgenden das dem Black/Scholes-Modell (BSM) zugrundeliegende Duplikationsprinzip erklärt werden (Cox, /Ross, /Rubinstein, 1979).
Angenommen Aktie und Call können nur zum Bewertungszeitpunkt und am Verfalltag gehandelt werden. Alle Marktteilnehmer stimmen darin überein, dass bis zum Verfalltag einer Option der aktuelle Kurs der Aktie S entweder auf den Wert Su ≡ U · S steigt oder auf den Wert Sd ≡ D · S fällt. Mit welcher Wahrscheinlichkeit der eine oder der andere Fall eintritt, spielt bei der weiteren Betrachtung keine Rolle. Der Gegenwartswert der Optionen hängt dann (bei gegebenem Diskontierungsfaktor) jeweils nur von den zwei Ausübungswerten Cu ≡ max{0, Su – K} und Cd ≡ max{0, Sd – K} ab, deren Wert wiederum vom Aktienkurs am Verfalltag abhängt. Das Ausübungswertprofil des Calls lässt sich durch das Liquidationswertprofil einer teilweise kreditfinanzierten Aktienanlage exakt duplizieren.
Technisch gesprochen existiert also immer ein Duplikationsportefeuille aus αS Aktien und αB Nullkupon-Anleihen (αB < 0 entspricht einer Kreditaufnahme), dessen Liquidationswertprofil am Periodenende mit dem des Calls übereinstimmt. Besitzt die Null-Kuponanleihe den gegenwärtigem Kurswert 1 und den Rückzahlungsbetrag r > 1, dann wählt man αS und αB derart, dass sowohl αS Su + αB R = Cu als auch αS Sd + αB R = Cd gilt. Es ergibt sich folgende Duplikationsstrategie:
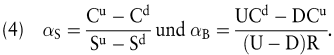
αS wird dabei als Hedge-Kennzahl (\'Delta\') bezeichnet. In arbitragefreien Finanzmärkten muss nun der Gegenwartswert des Duplikationsportefeuilles mit dem des Calls übereinstimmen:
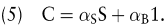
Mit der Vereinbarung p ≡ (R – D)/(U – D) und daher (1 – p) ≡ (U – R)/(U – D) gilt schließlich für den Wert des Calls
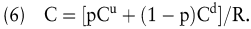
An einem Beispiel soll das hinter der Bewertungsformel (6) stehende Duplikationsprinzip noch erläutert werden. Zu bewerten sei ein Call auf eine Aktie, deren Kurswert am Periodenende bzw. am Fälligkeitstag des Calls entweder den Wert Su = 240 oder den Wert Sd = 160 annehmen kann. Beträgt der aktuelle Kurswert der Aktie S = 200 und verzinst sich eine risikofreie Finanzanlage mit 10% in der betrachteten Periode, dann gilt p = 0,75 und 1 – p = 0,25 wegen R = 1,10, U = 1,20 und D = 0,80. Bei einem Basispreis von K = 200 gilt für den Ausübungswert des Calls Cu = 40 bzw. Cd = 0 und folglich für den aktuellen Modellwert C = 27,27. Falls der beobachtete Callpreis diesen Modellwert übersteigt, dann ist die in Abb. 2 dargestellte Arbitragestrategie profitabel. Falls dagegen der Modellwert den Callpreis übersteigt, so ist die entsprechende Umkehrung dieser Strategie profitabel. 
Abb. 2: Profitable Zeitarbitrage falls der Callpreis seinen Modellwert übersteigt
In arbitragefreien Finanzmärkten müssen die Parameter p und (1 – p) zwischen 0 und 1 liegen und können damit als Wahrscheinlichkeiten interpretiert werden. In einem formalen Sinne entspricht dann der Wert des Calls dem diskontierten Erwartungswert des Ausübungswertes des Calls am Verfalltag:
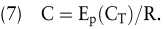
Die p entsprechende Verteilung wird deswegen auch risikoneutrale Verteilung genannt. Dies bedeutet allerdings nicht, dass die Optionsbewertung unter der Annahme der Risikoneutralität der Marktteilnehmer erfolgt, da die beschriebene Erwartungswertbildung eben auf der Basis der risikoneutralen Verteilung – die nicht mit der tatsächlichen übereinstimmen muss – erfolgt: Der Call wird also nur so bewertet, als ob die Marktteilnehmer risikoneutral wären. Aufgrund der benutzten Arbitrage- und Duplikationsargumente ist dieser Ansatz auch bei beliebig anderen Präferenzen der Marktteilnehmer (sofern diese mit der Arbitragefreiheit des Finanzmarktes verträglich sind) gültig. Man spricht bei p auch von einem äquivalenten Martingalmaß (Jarrow, R./Turnbull, S. 1996). Für einen viel allgemeineren Modellrahmen beweisen Harrison und Pliska (Harrison, J./Pliska, S. 1981) die folgende Aussage: die Existenz eines äquivalenten Martingalmaßes ist (im Wesentlichen) äquivalent zur Arbitragefreiheit des Finanzmarktes; seine Eindeutigkeit ist äquivalent zur Möglichkeit, jede Option durch Duplikation zu bewerten. Letzteres ist beispielsweise nicht möglich, wenn im vorangehenden Beispiel drei mögliche Aktienkurse am Verfalltag zugelassen werden.
b) Dynamische Duplikationsstrategie
Unterstellt man nun n Teilperioden bzw. n + 1 Handelszeitpunkte bis zum Verfalltag, wobei zwischen benachbarten Handelszeitpunkten entweder ein Kursanstieg oder ein Kursrückgang mit konstanter prozentualer Höhe zugelassen wird, dann gibt es zum k-ten Handelszeitpunkt genau k mögliche Aktienkurse. Ausgehend von den n + 1 möglichen Ausübungswerten am Verfalltag können dann für die n möglichen Aktienkurse am vorletzten Handelszeitpunkt die zugehörigen Callwerte durch n-fache Anwendung der Bewertungsformel (6) bestimmt werden. Die retrograde Anwendung dieses Bewertungsschemas führt dann schließlich zur Bewertungsformel:
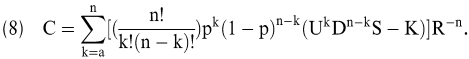
wobei der ganzzahlige Parameter a so bestimmt ist, dass für k ≥ a Kursanstiege während der Laufzeit die Kaufoption im Geld endet, d.h. Uk Dn-k S-K > 0 für k = a, ?, n gilt. In Übereinstimmung mit dem Einperiodenfall ist der Betrag C genau der Eigenmitteleinsatz, der benötigt wird, um das Ausübungswertprofil des Calls durch einen teilweise kreditfinanzierten Aktienkauf zu duplizieren. Im Unterschied zum Einperiodenfall muss jedoch zu jedem Handelszeitpunkt vor dem Verfalltag der Bestand an Aktien und Nullkupon-Anleihen im Duplikationsportefeuille durch Kauf oder Verkauf in Abhängigkeit der Aktienkursentwicklung angepasst werden. Diese Umschichtungsstrategie wird selbstfinanzierend genannt, weil ein Aktienkauf durch einen entsprechenden Verkauf von Nullkupon-Anleihen (und umgekehrt) finanziert wird (siehe Trautmann, 2006). c) Black/Scholes Formel für Calls
Fischer Black und Myron Scholes legen ihrem Modell einen stetigen Aktienkursverlauf mit konstanter Renditevolatilität zugrunde. Aktienkursrenditen sind normalverteilt mit dem annualisierten Mittelwert μ und der annualisierten Standardabweichung σ, auch Volatilität genannt. Sie zeigen, dass bei einer zeitstetigen Anpassung des Duplikationsportefeuilles der Callwert einer analytisch lösbaren partiellen Differentialgleichung genügt. Wählt man nun in Formel (8) R = exp(rT/n), U = exp(∼ 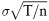 ) und D = exp(∼ – ) und D = exp(∼ – 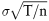 ), dann erhält man für n →∞ ebenfalls die Black/Scholes-Formel für Calls vom europäischen Typ: ), dann erhält man für n →∞ ebenfalls die Black/Scholes-Formel für Calls vom europäischen Typ:
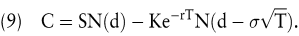
wobei d = (ln(S/K) + (r + 0,5 σ2) T)/ 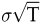 . Neben den bereits eingeführten Symbolen bezeichnet in der Formel N(·) die Verteilungsfunktion einer standard-normalverteilten Zufallsvariablen und r = lnR die zeitstetige Verzinsungsrate. . Neben den bereits eingeführten Symbolen bezeichnet in der Formel N(·) die Verteilungsfunktion einer standard-normalverteilten Zufallsvariablen und r = lnR die zeitstetige Verzinsungsrate.
Der durch Gleichung (9) gegebene Wert eines Calls kann intuitiv interpretiert werden als die gewichtete Differenz zwischen Aktienkurs und Barwert des Basispreises, wobei die Gewichte N(d) und N(d- 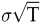 Werte zwischen null und eins annehmen können. Im Falle einer weit aus dem Geld notierenden Option (d.h. S ist viel kleiner als K) ist der Call beinahe wertlos, weil beide Gewichte nahe bei null liegen. Ist die Option hingegen tief im Geld (d.h. S ist viel größer als K), so nehmen beide Gewicht Werte nahe eins an, und der Wert der Option entspricht in etwa der europäischen Wertuntergrenze (1). Werte zwischen null und eins annehmen können. Im Falle einer weit aus dem Geld notierenden Option (d.h. S ist viel kleiner als K) ist der Call beinahe wertlos, weil beide Gewichte nahe bei null liegen. Ist die Option hingegen tief im Geld (d.h. S ist viel größer als K), so nehmen beide Gewicht Werte nahe eins an, und der Wert der Option entspricht in etwa der europäischen Wertuntergrenze (1).
Der Wert eines Calls hängt gemäß der Black/Scholes Formel (9) von den folgenden fünf Parametern ab: dem aktuellen Aktienkurs S, dem Basispreis K, der Restlaufzeit T, der Verzinsungsrate für eine risikolose Anlage r und der zukünftigen Volatilität σ der zugrundeliegenden Aktie. Lediglich der letzte der genannten Parameter ist nicht direkt beobachtbar. Überraschenderweise hängt der Wert eines Calls nicht direkt von der erwarteten Aktienrendite ab. Diese hat über den beobachteten Aktienkurs nur einen indirekten Einfluss auf den Optionswert. Dies ist wohl der wesentliche Grund für die breite Akzeptanz dieses Bewertungsmodells in Theorie und Praxis.
Der Volatilitätsparameter kann prinzipiell auf zweierlei Arten geschätzt werden: auf der Basis der historischen Volatilität der zugrundeliegenden Aktie oder auf der Basis der so genannten impliziten Volatilität. Letztere wird durch die Gleichsetzung von Black/Scholes-Formel und Marktpreis mit anschließender (numerischer) Auflösung der Gleichung nach dem Volatilitätsparameter bestimmt. d) Bewertung amerikanischer Puts
Bei Kenntnis des Callwerts lässt sich der Wert eines europäischen Puts mittels der Put-Call-Parität einfach bestimmen. Die Bewertung eines amerikanischen Puts muss dagegen derart erfolgen, dass der Putwert in jedem Zeitpunkt und für jeden Aktienkurs den entsprechenden Ausübungswert nicht unterschreitet. Da für dieses Problem bis heute keine analytische Lösung bekannt ist, begnügt man sich mit approximativen, analytischen Lösungen bzw. verwendet numerische Lösungsansätze. Letztere basieren z.B. auf dem Binomialmodell für Puts oder lösen die partielle Differentialgleichung für den Put numerisch (Hull, J. 1997; Stoll, H.R./Whaley, R.E. 1993).
2. Alternative Bewertungsmodelle für Aktienoptionen
Im BSM besitzen Aktienkurse stetige Kursrealisierungen mit konstanter Volatilität. Ferner ist die Verzinsung von insolvenzrisikofreien Anlagen konstant und es gibt keine Dividenden und keine Transaktionskosten. Eine Reihe von Modellvarianten heben diese restriktiven Annahmen auf. So wurden Aktienkursprozesse mit zufälliger Volatilität mit und ohne Kurssprünge betrachtet. Solange über infinitesimal kleine Zeitspannen Änderungen der Volatilität mit Änderungen des Aktienkurses perfekt korreliert sind (perfekte Momentankorrelation), kann auch bei diesen Modellvarianten das Duplikationsprinzip zur Anwendung gelangen. Dies ist dann der Fall, wenn die Volatilität eine deterministische Funktion des Aktienkurses ist, wie dies im constant elasticity of variance model von Cox und Ross (Cox, J./Ross, S. 1976) unterstellt wird. Eine negative Elastizität motiviert Geske (Geske, R. 1979) in seinem compound option model mit einem Kapitalstrukturargument, während Rubinstein in seinem displaced diffusion model (Cox, /Rubinstein, 1985) eine positive Elastizität mit einem Vermögensstrukturargument begründet.
Stochastische Änderungen der zeitstetigen Verzinsungsrate wurden bereits in einer frühen Modellvariante von Merton (Merton, 1973) zugelassen. Zu diskreten Zeitpunkten anfallende Dividenden konnten zunächst nur im Rahmen numerischer Ansätze berücksichtigt werden. Mittlerweile stehen auch approximative Bewertungsformeln zur Verfügung (Stoll, H.R./Whaley, R.E. 1993). Die modellmäßige Erfassung von Transaktionskosten gelingt Boyle und Vorst (Boyle, P./Vorst, T. 1992) in einem zeitdiskreten Modell. Diese führt zu einer oberen bzw. unteren Wertgrenze durch die transaktionskostenabhängige Anpassung des Volatilitätsparameters.
3. Bewertungsmodelle für sonstige Finanztitel
Die Übertragung des BSM erfolgte auf eine Vielzahl anderer Instrumente. Bei der Bewertung europäischer Optionen auf Devisen und Futures sind nur geringfügige Modifikationen erforderlich. Für entsprechende Optionen vom amerikanischen Typ, deren frühzeitige Ausübung auch im Fall von Calls jederzeit lohnenswert sein kann, stehen approximative Formeln zur Verfügung (Stoll, H.R./Whaley, R.E. 1993).
Im Zusammenhang mit der Bewertung von Optionen auf eine Anleihe liegt es nahe, nach dem Vorbild des BSM für Aktienoptionen, diese auf der Grundlage der stochastischen Entwicklung des Anleihenkurses zu bewerten. Eine konsistente Bewertung von Zinsoptionen kann jedoch nur über die arbitragefreie Modellierung der Entwicklung zukünftiger Zinsstrukturen erfolgen. Zudem sollte es möglich sein, diese ausgehend von der aktuell beobachtbaren Zinsstrukturkurve zu modellieren. Die älteren Ansätze zur Charakterisierung des stochastischen Übergangsverhaltens von Zinsstrukturkurven verletzen die zweite Forderung und führen zu Bewertungsbeziehungen, in denen zudem explizit präferenzabhängige Parameter enthalten sind. Die von Heath, Jarrow, Morton (Heath, J./Jarrow, R./Morton, A. 1992) vorgeschlagene Modellklasse umfasst Modelle, die beide Bedingungen erfüllen (z.B. Ho, T./Lee, S. 1986; Hull, J./White, A. 1990; Miltersen, K.R./Sandmann, K./Sondermann, D. 1997).
In ihrer bahnbrechenden Arbeit weisen Black und Scholes bereits darauf hin, dass auch optionsähnliche Ansprüche mit ihrer Methode bewertet werden können. Dazu zählen insbesondere alle Formen des Eigen- und Fremdkapitals einer Unternehmung, die als Optionen oder Portefeuilles von Optionen auf das Vermögen einer Unternehmung aufgefasst werden können. Die Nichtbeobachtbarkeit der Vermögensrendite erschwert jedoch sehr oft die direkte Anwendung des BSM auf der Basis historischer Volatilitäten (Schulz, G.U./Trautmann, S. 1994).
IV. Gleichgewichts- und sonstige Modelle
Das Duplikationsprinzip versagt, wenn mehrere exogene Risikoquellen existieren. Dies ist z.B. der Fall, wenn Kurssprünge auftreten oder die Momentankorrelation zwischen stochastischer Volatilität und Aktienkurs nicht perfekt ist. Die vorgeschlagenen OBM basieren auf präferenzabhängigen Gleichgewichtsmodellen (Cox, J./Ingersoll, J./Ross, S. 1985; Schöbel, R. 1995) oder unterstellen, dass Volatilitäts- bzw. Kurssprungrisiken diversifizierbar sind. Es stellt sich dann die Frage, wie der Verkäufer einer Option sich gegen eine spätere Inanspruchnahme am besten schützen kann (siehe Grünewald, /Trautmann, 1997; Schulmerich, /Trautmann, 2003)
1. Präferenzunabhängige Modelle
Die Präferenzabhängigkeit der Bewertung lässt sich vermeiden, wenn man z.B. das exogene Volatilitätsrisiko als diversifizierbar unterstellt. In seinem präferenzunabhängigen Modell lässt Merton (Merton, R.C. 1976) die stetigen Kurspfade des BSM durch Kurssprünge überlagern, unterstellt aber gleichzeitig die Diversifizierbarkeit des Kurssprungrisikos. Hull und White (Hull, /White, 1987) zeigen ebenfalls für ein Modell mit stochastischer Volatilität die wünschenswerte Präferenzunabhängigkeit, falls Volatilität und aggregierter Konsum unkorreliert sind.
2. Präferenzabhängige Modelle
Rubinstein (Rubinstein, M. 1976) zeigte als erster, dass die präferenzfreie Black/Scholes-Formel auch dann noch Gültigkeit besitzen kann, falls im BSM die Annahme der zeitstetigen Handelbarkeit von Aktie und Option aufgegeben wird. Dazu unterstellt er im Rahmen eines Gleichgewichtsmodells, die Existenz eines repräsentativen Investors mit logarithmischen Präferenzen. Wird jedoch die im BSM unterstellte Annahme der Lognormalverteilung der Aktienkurse aufgegeben, dann resultieren daraus in der Regel Bewertungsformeln, die nicht frei von Präferenzparametern sind (Bates, D.S. 1991; Heston, S.L. 1993; Carr, /Geman, /Madan, /Yor, 2002). Eine Ausnahme bildet das Modell von Duan (Duan, J.-C. 1995).
V. Empirische Überprüfung
1. Modellunabhängige Wertgrenzen
Die Profitabilität von Arbitragestrategien, wurde sowohl im Rahmen von ex-post-Tests als auch im Rahmen von ex-ante-Tests überprüft. Ex-post-Tests unterstellen, dass (1) die beobachteten Preise für Optionen und Basisinstrument zeitgleich festgelegt worden sind und (2) im Falle von fehlbewerteten Optionen noch zu den Preisen, die eine Fehlbewertung anzeigen, eine die Fehlbewertung ausnutzende Arbitrageposition hätte aufgebaut werden können. Ein ex-ante-Test berücksichtigt demgegegenüber (1) die meist nichtsimultane Festlegung von Preisen für Optionen und des zugrundeliegenden Basisinstruments, sowie (2) einen Zeitabstand zwischen dem Erkennen eines Fehlbewertungssignals und dem Aufbau einer entsprechenden Portefeuilleposition. Die empirischen Ergebnisse dazu lassen durchaus den Schluss zu, dass unter Berücksichtigung von Transaktionskosten Optionsmärkte im großen und ganzen informationseffizient sind. Aber auch für diejenigen Märkte und Teilperioden, in denen eine ökonomisch signifikante Profitabilität festgestellt werden konnte, muss bedacht werden, dass ein angemessener Anteil des errechneten \'Arbitragegewinns\' als Kompensation für das Preisänderungsrisiko, das durch den nichtsimultanen Aufbau des Arbitrageportefeuilles entsteht, aufgefasst werden kann (Bhattacharya, M. 1983; Trautmann, S. 1986; Trautmann, S. 1989).
2. Bewertungsmodelle
Der Vergleich von Marktpreisen mit korrespondierenden Black/Scholes-Modellwerten für Optionen zeigt immer wieder, dass Letztere die Marktpreise im Mittel sehr gut erklären können. Dennoch liegt keine unverzerrte Erklärung von Marktpreisen vor, denn diese würde z.B. bedeuten, dass die implizite Volatilität auf der Basis beobachteter Marktpreise für Optionen unabhängig ist von den Modellparametern Basispreis und Restlaufzeit. Die bekannteste Verzerrung wird durch den U-förmigen Zusammenhang zwischen der impliziten Volatilität und dem Verhältnis von Aktienkurs und Basispreis (money-ratio) beschrieben (Smile-Effekt). Demzufolge ist die implizite Volatilität besonders niedrig für Optionen, die am Geld notieren, während sie für Optionen, die entweder tief im Geld oder tief aus dem Geld sind, besonders hoch ist. Dieser typische Zusammenhang verflacht allerdings mit zunehmender Restlaufzeit (Hull, J. 1997). Auch alternative OBM weisen Verzerrungen der einen oder anderen Art auf. Rubinstein (Rubinstein, M. 1985); Longstaff (Longstaff, F. 1995); Bakshi/Cao/Chen (Bakshi, G./Cao, C./Chen, Z. 1997) und Trautmann/Beinert (Trautmann, S./Beinert, M. 1999) präsentieren entsprechende Ergebnisse für Aktienoptionen und Bühler/Uhrig-Homburg/Walter/Weber (Bühler, W./Uhrig-Homburg, M./Walter, U./Weber, T. 1999) für Zinsoptionen.
Literatur:
Bachelier, L. : Théorie de la spéculation, in: Annales de l\'Ecole Normale Superieure 1900, S. 21 – 86
Bakshi, G./Cao, C./Chen, Z. : Empirical Performance of Alternative Option Pricing Models, in: JF 1997, S. 2003 – 2049
Bates, D.S. : The Crash of \'87: Was It Expected? The Evidence from Options Markets, in: JF 1991, S. 1009 – 1044
Bhattacharya, M. : Transactions Data Tests of Efficiency of the Chicago Board Options Exchange in: JFE 1983, S. 161 – 185
Black, F./Scholes, M. : The Pricing of Options and Corporate Liabilities, in: JPol.E 1973, S. 637 – 659
Boness, A.J. : Elements of a theory of stock option value, in: JPol.E 1964, S. 163 – 175
Boyle, P./Vorst, T. : Option Replication in Discrete Time with Transaction Costs, in: JF 1992, S. 271 – 293
Bühler, W./Uhrig-Homburg, M./Walter, U./Weber, T. : An Empirical Comparison of Forward-Rate and Spot-Rate Models for Valuing Interest-Rate Options, in: JF 1999, S. 269 – 305
Carr, P./Geman, H./Madan, D./Yor, M. : The Fine Structure of Asset Returns, in: An Empirical Investigation, in: JB 2002; S. 305 – 332
Cox, J./Ross, S. : The Valuation of Options for Alternative Stochastic Processes, in: JFE 1976, S. 145 – 166
Cox, J./Ingersoll, J./Ross, S. : An Intertemporal General Equilibrium Model of Asset Prices, in: ENM 1985, S. 363 – 384
Cox, J./Ross, S./Rubinstein, M. : Option Pricing: A Simplified Approach, in: JFE 1979; S. 229 – 263
Duan, J.-C. : The GARCH Option Pricing Model, in: Mathematical Finance 1995, S. 13 – 32
Geske, R. : The Valuation of Compound Options, in: JFE 1979, S. 63 – 81
Grünewald, B./Trautmann, S. : Varianzminimierende Hedgingstrategien für Optionen bei möglichen Kurssprüngen, in: ZfbF, Sonderheft 38, 1997, S. 43 – 87
Harrison, J./Pliska, S. : Martingales and Stochastic Integrals in the Theory of Continuous Trading, in: Stochastic Processes and their Applications 1981, S. 215 – 260
Heath, J./Jarrow, R./Morton, A. : Bond Pricing and the Term Structure of Interest Rates: A New Methodology for Contingent Claims Valuation, in: ENM 1992, S.77 – 105
Heston, S.L. : A Closed-Form Solution for Options with Stochastic Volatility with Applications to Bond and Currency Options, in: RoFS 1993, S. 327 – 343
Ho, T./Lee, S. : Term Structure Movements and Pricing Interest Rate Contingent Claims, in: JF 1986, S. 1011 – 1029
Hull, J. : Options, Futures and Other Derivative Securities, Englewood Cliffs 1997, 3. A
Hull, J./White, A. : Pricing Interest-Rate-Derivative Securities, in: RoFS 1990, S. 573 – 592
Hull, J./White, A. : The Pricing of Options on Assets with Stochastic Volatilities, in: JF 1978, S. 281 – 300
Jarrow, R./Turnbull, S. : Derivative Securities, Cincinnati 1996
Longstaff, F. : Option Pricing and the Martingale Restriction, in: RoFS 1995, S. 1091 – 1124
Mason, S./Merton, R.C. : The Role of Contingent Claims Analysis in Corporate Finance, in: Recent Advances in Corporate Finance, hrsg. von Altmann, E./Subrahmanyam, M., Homewood 1985, S. 7 – 54
Merton, R.C. : Theory of Rational Option Pricing, in: Bell Journal of Economics and Management Science 1973, S. 141 – 183
Merton, R.C. : Option Pricing When Underlying Stock Returns are Discontinuous, in: JFE 1976, S. 125 – 144
Miltersen, K.R./Sandmann, K./Sondermann, D. : Closed Form Solutions for Term Structure Derivatives with Log-Normal Interest Rates, in: JF 1997, S. 409 – 430
Rubinstein, M. : The valuation of uncertain income streams and the pricing of options, in: Bell Journal of Economics 1976, S. 407 – 25
Rubinstein, M. : Nonparametric Tests of Alternative Option Pricing Models Using all Reported Trades and Quotes on the 30 Most Active CBOE Option Classes from August 23, 1976 through August 31, 1978, in: JF 1985, S. 455 – 480
Samuelson, P.A. : Rational theory of warrant pricing, in: Industrial Management Review 1965, S. 13 – 32
Samuelson, P.A./Merton, R.C. : A complete model of warrant pricing that maximizes utility, in: Industrial Management Review 1969, S. 17 – 46
Schöbel, R. : Kapitalmarkt und zeitkontinuierliche Bewertung, Heidelberg 1995
Schulmerich, M./Trautmann, S. : Local Expected Shortfall-Hedging, in: European Finance Review 2003; S. 75 – 102
Schulz, G.U./Trautmann, S. : Robustness of Option-like Warrant Valuation, in: JBF 1994, S. 841 – 859
Sprenkle, C.M. : Warrant prices as indicators of expectations and preferences, in: Yale Economic Essays 1961, S. 178 – 231
Stoll, H. : The Relationship between Put and Call Options Prices, in: JF 1969, S. 802 – 824
Stoll, H.R./Whaley, R.E. : Futures and Options, Ohio 1993
Trautmann, S. : Finanztitelbewertung bei arbitragefreien Finanzmärkten, Habil. Karlsruhe 1986
Trautmann, S. : Aktienoptionspreise an der Frankfurter Optionsbörse im Lichte der Optionsbewertungstheorie, in: FuPM 1989, S. 210 – 225
Trautmann, S. : Investitionen – Bewertung, Auswahl und Risikomanagement, Berlin 2006
Trautmann, S./Beinert, M. : Impact of Stock Price Jumps on Option Values, in: Empirical Research on German Capital Markets, hrsg. von Bühler, W./Hax, H./Schmidt, R.1999, S. 303 – 322
|