|
Informationstheorie
Inhaltsübersicht
I. Einführung
II. Mathematische Informationstheorie und statistischer Informationsgehalt
III. Ökonomische Ansätze
I. Einführung
Im Folgenden wird zwischen der mathematischen und der ökonomischen Informationstheorie unterschieden. Die beiden Ausrichtungen lassen sich mit Hilfe der Semiotik (Sprachtheorie), die drei Ebenen einer Nachricht differenziert, abgrenzen:
| - | die Zeichenfolge (syntaktische Ebene), | | - | die Bedeutung der Zeichen bzw. der Nachricht (semantische Ebene), | | - | die Verwendung der Nachricht durch Sender und Empfänger (pragmatische Ebene). |
Die mathematische Informationstheorie beschränkt sich auf die syntaktische Ebene, d.h. sie abstrahiert von der Bedeutung und der Verwendung einer Nachricht. Sie ist ein Teilgebiet der mathematischen Statistik und beschäftigt sich vornehmlich mit technisch-statistischen Problemen, wie z.B. der Übertragung, Speicherung und Kompression von Zeichenfolgen sowie der Messung des statistischen Informationsgehaltes von Nachrichten (z.B. Maasoumi, E. 1987).
Die ökonomische Informationstheorie bezieht sich vornehmlich auf die pragmatische Ebene, d.h. die Verwendung einer Nachricht. Daher versteht man unter Information i.d.R. zweckorientiertes Wissen, wobei der Zweck die Vorbereitung von Entscheidungen und Handlungen ist (z.B. Wittmann, W. 1959). Information kann daher auch als entscheidungsorientiertes Wissen definiert werden (z.B. Mag, W. 1977). Ob eine Nachricht auch eine Information darstellt, hängt aber nicht nur von ihrer Verwendung, sondern auch vom Vorwissen des Entscheiders ab. Eine Nachricht muss neu ( „ news “ ) sein, d.h. nur der nicht redundante Teil der Nachricht stellt Information dar. Unter Kommunikation versteht man i. Allg. die (intersubjektive) Übermittlung von Informationen.
Innerhalb der ökonomischen Informationstheorie wird zum einen das Problem analysiert, ob für eine Entscheidung zusätzliche Informationen eingeholt werden sollen. Hierzu ist der ökonomische Wert der Information aus Sicht des Entscheiders zu bestimmen. Zum anderen werden Informationsprobleme und ihre Konsequenzen auf Märkten und in Vertragsbeziehungen, also bei Interaktion mehrerer Personen, behandelt.
II. Mathematische Informationstheorie und statistischer Informationsgehalt
Der Informationsgehalt einer Nachricht bezüglich eines unsicheren Ereignisses wird i. Allg. über die Verringerung der Unsicherheit durch den Erhalt der Nachricht gemessen. Man benötigt also ein Maß für die Unsicherheit, welche i.d.R. über Wahrscheinlichkeitsverteilungen ausgedrückt wird. Als ein solches Maß liefert die mathematische Informationstheorie die Entropie einer Wahrscheinlichkeitsverteilung (Shannon, C./Weaver, W. 1949), die auch als Shannon\'sche Information bezeichnet wird. Sie wird mit Hilfe von Informationsfunktionen ermittelt, die axiomatisch abgeleitet sind. Im Allgemeinen wird verlangt, dass die Informationsfunktion kontinuierlich, additiv für unabhängige Ereignisse sowie monoton abnehmend in der Wahrscheinlichkeit des Ereignisses ist. Es lässt sich zeigen, dass diese Axiome die Funktion – log(·) eindeutig identifizieren, wobei die Basis des Logarithmus die Maß- oder Informationseinheit festlegt (z.B. Maasoumi, E. 1987). Wählt man z.B. den dyadischen Logarithmus (log2), so wird der Informationsgehalt in bits, also in binären Einheiten, gemessen.
Gewichtet man die Informationsfunktion mit den Eintrittswahrscheinlichkeiten der Ereignisse, erhält man die Entropie einer (diskreten) Wahrscheinlichkeitsverteilung:
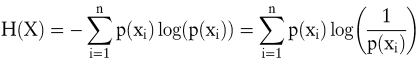
wobei p(xi) für die Wahrscheinlichkeit des Ereignisses xi ∊ X und n für die Anzahl der möglichen Ereignisse stehen. Die Entropie (oder Unsicherheit) ist maximal, wenn jedes Ereignis gleich wahrscheinlich ist, d.h. eine Gleichverteilung vorliegt. In diesem Fall vereinfacht sich der Ausdruck zu: H(X) = log n. Folglich spielt neben der Verteilung auch die Anzahl der möglichen Ereignisse eine entscheidende Rolle.
Betrachten wir dazu ein Beispiel: Das Ereignis xi sei die Seitenzahl der aufgeschlagenen Seite eines Lexikons. Sofern diese zufällig aufgeschlagen wurde, sind alle Seitenzahlen gleich wahrscheinlich. Die Unsicherheit über die aufgeschlagene Seite nimmt mit der Anzahl der Seiten des Lexikons zu und entspricht ihrem Logarithmus. Was genau gibt uns diese Zahl aber an? Stellen wir uns vor, dass eine andere Person die Seitenzahl erfragen soll, aber nur Fragen stellen darf, die mit Ja oder Nein zu beantworten sind. H(X) gibt dann an, wie viele Ja-Nein Fragen diese Person bei optimaler Fragestrategie mindestens stellen müsste, um die Seitenzahl herauszufinden. Für ein Buch mit 1024 Seiten wären somit mindestens log2(1024) = 10 Fragen zu stellen, wobei die Basis 2 verwendet wird, weil die Antwort binär ist. Wurde die Seite dagegen nicht zufällig aufgeschlagen und kann die fragende Person ungefähr einschätzen, ob die gewählte Seite eher am Anfang oder Ende des Lexikons liegt, dann ist es möglich, mit weniger als 10 Fragen auszukommen. In diesem Fall gibt H(X) an, wie viele Fragen im Durchschnitt zu stellen sind, wenn man die (ungleiche) Wahrscheinlichkeitsverteilung der Seitenzahlen optimal ausnutzt.
Der statistische Informationsgehalt einer Nachricht yi bezüglich einer Zufallsvariablen X lässt sich nun als Differenz der Entropie vor und nach Erhalt der Nachricht messen, wobei Letztere für die bedingte Verteilung zu ermitteln ist (z.B. van der Lubbe, J.C. 1997). Der Informationsgehalt ist maximal, wenn wir vor Erhalt der Nachricht yi ∊ Y alle Umweltzustände für gleich wahrscheinlich halten und danach das Ereignis xi ∊ X mit Sicherheit kennen. Er ist null, wenn die Nachricht und das Ereignis stochastisch unabhängig sind. Der Informationsgehalt ist also entscheidend vom (stochastischen) Zusammenhang von Nachricht und Ereignis, welcher durch die gemeinsame Verteilung p(x,y) beschrieben wird, abhängig. Diesen Zusammenhang und das Set möglicher Nachrichten bezeichnet man als die Informationsstruktur einer Nachrichtenquelle: {Y, p(x,y)}.
Ein Ranking von Nachrichtenquellen bzw. Informationsstrukturen nach ihrem Informationsgehalt ist unabhängig von ihrer Verwendung mithilfe von Dominanzkriterien möglich. Ein solches Kriterium formuliert das Blackwell-Theorem, wonach – etwas vereinfacht – eine Informationsstruktur I einer anderen I′ vorzuziehen ist, wenn I′ für jede Nachricht von I lediglich eine Verteilung von Nachrichten liefert (Blackwell, D. 1953). Lässt sich also eine Struktur I′ aus einer anderen Struktur I durch Aggregation des Nachrichtenraums erzeugen, dann ist I die feinere Struktur und zu bevorzugen: z.B. I = {y1, y2, y3, y4} und I′={y′1, y′2}={(y1, y4), (y2, y3)}. Ferner gilt, dass eine nach dem Blackwell-Kriterium bevorzugte Struktur zu einer größeren (erwarteten) Verringerung der Entropie führt (vgl. Lawrence, D.B. 1999, S. 203).
In vielen Fällen sind die Informationsstrukturen jedoch nicht mithilfe des Blackwell-Kriteriums vergleichbar. Ein Ranking erfordert dann eine Bewertung der Informationsstrukturen, was i.d.R. nur für die konkrete Entscheidungssituation, also auf der pragmatischen Ebene, möglich ist. Dieses Problem wird im nächsten Abschnitt behandelt. Der Informationsgehalt ist daher im Regelfall nicht mit dem Informationswert gleichzusetzen. Allerdings lässt sich in einigen Fällen über die Mengenebene eine Beziehung zu den Informationskosten herstellen. So kann der Informationsgehalt (bzw. die Shannon\'sche Information) auch als Informationsmenge interpretiert und zur Bestimmung der Informationskosten (z.B. durch Multiplikation mit dem Kostensatz pro übertragene Informationseinheit) herangezogen werden (Mag, W. 1977, S. 154 ff.).
III. Ökonomische Ansätze
1. Informationsakquisition für Individualentscheidungen und Informationswert
Informationen sind ein wesentlicher Input für Entscheidungen. Da sie aber nicht in beliebigem Umfang zur Verfügung stehen, stellt sich das Problem, ob vor einer Entscheidung zusätzliche Informationen beschafft werden sollen. Die Akquisition von Informationen ist i.d.R. nicht kostenlos, wobei sowohl Ausgaben als auch Opportunitätskosten (z.B. in Form von Zeit) entstehen können. Die Entscheidung über eine Informationsakquisition erfordert daher ein Abwägen der Kosten und des Wertes der Informationen (z.B. Laux, H. 1982). Da aber zu diesem Zeitpunkt noch nicht feststeht, zu welchem Ergebnis eine Informationsbeschaffung führt, handelt es sich um ein Entscheidungsproblem bei Risiko, welches mithilfe des Grundmodells der Entscheidungstheorie analysiert werden kann.
Informationen haben Wert, weil sie zumindest potenziell die Entscheidungen und damit die Handlungen des Entscheiders beeinflussen können. So können Informationen z.B. zu einer Revision des (a priori) Wahrscheinlichkeitsurteils und mithin zu einer veränderten Bewertung der Handlungsalternativen führen. Der Wert solcher Revisionen und damit der Informationen hängt vom konkreten Entscheidungsproblem, also u.a. den Handlungsalternativen und der Nutzenfunktion des Entscheiders, ab.
Konzeptionell ist der Informationswert für einen risikoneutralen Entscheider gleich der Differenz zwischen dem Erwartungswert des Erfolgs bei Entscheidung mit Information und dem Erwartungswert des Erfolgs bei Entscheidung ohne Information. Letzerer lässt sich wie folgt berechnen:
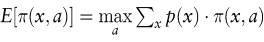
wobei π(·) für den Erfolg des Entscheiders, x für den Umweltzustand und a für die Handlungsalternative stehen. Die optimale Handlungsalternative nach Zugang der Information y ergibt sich bei Verwendung der a posteriori Wahrscheinlichkeitsverteilung der Umweltzustände p(x|y), die dem Theorem von Bayes folgend ermittelt wird:
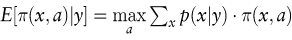
Da vor der Informationsbeschaffung noch nicht feststeht, welche Information der Entscheider erhält, ist E[π(x,a)|y] für alle möglichen Informationsergebnisse zu berechnen, wobei gemäß dem Prinzip der flexiblen Planung für jedes y die optimale Handlungsalternative gewählt wird. Anschließend ist E[π(x,a)|y] mit den Eintrittswahrscheinlichkeiten der Informationsergebnisse zu gewichten, um den Erwartungswert des Erfolgs mit Information zu berechnen. Der ökonomische Informationswert (vor Abzug von Informationskosten) ist dann die Differenz der beiden Erwartungswerte (Marschak, J. 1954):
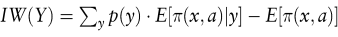
Der Informationswert kann als der Betrag interpretiert werden, den der (risikoneutrale) Entscheider maximal bereit ist, für eine Informationsquelle zu bezahlen (Grenzpreis). Er kann nicht negativ sein, weil der Entscheider stets auf die Verwendung der Informationen verzichten und damit E[π(x,a)] realisieren kann. Die Obergrenze für den Informationswert ist dagegen der Wert perfekter Information (Marschak, J. 1974). Die Beschaffung einer Information ist also nur dann vorteilhaft, wenn der Informationswert die Informationskosten übersteigt. Prinzipiell sind so lange neue Informationen einzuholen, bis die Grenzkosten neuer Informationen gleich ihrem Grenznutzen, d.h. ihrem Grenzinformationswert sind (Stigler, G.J. 1961).
Die explizite Berechnung des Informationswertes ist i.d.R. sehr komplex, weil das Informations- und das Entscheidungsproblem nur simultan gelöst werden können. Die Entscheidung über die Informationsbeschaffung stellt daher ein Metaproblem dar. Fragt man nun, ob für diese Entscheidung ebenfalls Informationen (z.B. über mögliche Quellen) eingeholt werden sollen, führt dies zu einem Meta-Metaproblem und letztlich zum infiniten Regress. Die explizite Berechnung des Informationswertes dürfte daher in der Praxis selten möglich sein. Vielmehr zeigt die Entscheidungstheorie Determinanten des Informationswertes auf, die in praxi eine grobe Abschätzung des Informationswertes erlauben oder Hilfestellung beim Design von Informationssystemen geben.
Neben dieser eher normativen Analyse gibt es auch eine Reihe von empirischen Untersuchungen zum Informationsverhalten, auf die jedoch nicht eingegangen werden soll (vgl. hierzu Witte, E. 1972; Gemünden, H.-G. 1992; Lawrence, D.B. 1999, Kap. 9).
2. Informationsökonomie (Economics of Information)
Neben der soeben vorgestellten Theorie zum Informationsbeschaffungsproblem eines Entscheiders gibt es eine Reihe von Ansätzen, die sich mit den Konsequenzen unvollkommener Information auf Märkten und in Vertragsbeziehungen beschäftigen. Im Mittelpunkt der Analyse stehen also Informationsprobleme bei Interaktion mehrerer Personen. Die Theorie, die diese Probleme behandelt, wird häufig als Informationsökonomie bezeichnet. Man sollte mit diesem Begriff jedoch nicht die Vorstellung verbinden, es handele sich um ein spezielles Teilgebiet der ökonomischen Theorie, wie z.B. die Agrar- oder Industrieökonomie, weil die Auseinandersetzung mit Informationsproblemen zu einem zentralen Element der ökonomischen Analyse geworden ist. Im Folgenden werden drei wichtige Ansätze und ihre Problemstellungen vorgestellt (vgl. auch Stiglitz, J. 1985). a) Preis- und Qualitätssuche auf Märkten
Ausgangspunkt der Preissuchmodelle ist die Beobachtung, dass auf realen Märkten die Preise auch für homogene Güter i. Allg. von Anbieter zu Anbieter differieren. Nachfrager werden daher die Preise verschiedener Anbieter vergleichen wollen. Ein solcher Preisvergleich verursacht jedoch Kosten. Man kann daher fragen, wie dieser Suchprozess optimal zu gestalten ist. Er gilt, dass der optimale Stichprobenumfang mit der Streuung der Preise zu- und mit der Höhe der Suchkosten abnimmt (Stigler, G.J. 1961). Ferner kann man zeigen, dass ein sequenzieller Suchprozess mit Reservationspreis einer Suche mit optimalem Stichprobenumfang i.d.R. überlegen ist. Dies gilt auch dann, wenn der Nachfrager die Verteilung der Preise nicht genau kennt.
Man kann ferner fragen, welche Konsequenzen sich aus der Preissuche für das Marktgleichgewicht ergeben. Die Schwierigkeit besteht darin, dass die optimale Suchstrategie der Nachfrager und die optimalen Angebotspreise der Anbieter simultan festzulegen sind. Im Allgemeinen eliminiert die Preissuche der Nachfrager die ursprüngliche Preisdispersion. Der sich im Gleichgewicht einstellende Preis ist i.d.R. der Monopol- und nur in Ausnahmefällen der Wettbewerbspreis (z.B. Nermuth, M. 1982, m.w.N.).
Die Überlegungen zur Preissuche lassen sich ohne große Schwierigkeiten auch auf die Qualitätssuche übertragen, sofern die Qualität des Gutes im Kaufzeitpunkt überprüft werden kann. In diesem Fall verursacht die Qualitätssuche lediglich Suchkosten. b) Informationsproduktion, -akquisition und Offenlegung auf Märkten
Eine Reihe von Ansätzen beschäftigt sich mit der Informationsproduktion bzw. Informationsakquisition auf Märkten (Hirshleifer, J./Riley, J.G. 1992, Kap. 7, m.w.N.). Sie thematisieren, dass einmal geschaffenes Wissen ein „ public good “ ist: Es kann quasi beliebig kopiert und damit verwendet werden, ohne dass andere von der Verwendung ausgeschlossen wären. Die Anreize zur Informationsproduktion (z.B. Forschung) hängen daher entscheidend davon ab, wie die Verfügungsrechte an der Information (z.B. durch Patente) verteilt sind. Unvollkommene Verfügungsrechte erlauben anderen, die Information zu nutzen, und verringern somit den Anreiz, in die Generierung von Informationen zu investieren. Ein solcher positiver externer Effekt führt zu einer Informationsunterproduktion aus Sicht des sozialen Optimums (Arrow, K. 1962; Externe Effekte).
Ist der Informationsproduzent durch Verfügungsrechte gut geschützt, der Zugang zur Informationsquelle jedoch unbeschränkt, kommt es zur Informationsüberproduktion, wenn der private Wert der Information größer ist als ihr sozialer. Ein solcher negativer externer Effekt tritt auf, wenn die Informationsakquisition primär distributive Effekte hat. In Finanzmärkten z.B. verschafft die Informationsakquisition einem Investor primär Informationsvorteile gegenüber anderen uninformierten Investoren; der soziale Wert der Information ist dagegen (nahezu) null. Die private Informationsbeschaffung ist daher – sofern sie Kosten verursacht – sozial unerwünscht.
Die beschriebenen Effekte stehen in engem Zusammenhang mit der Offenlegung der Informationen. Positive externe Effekte bestehen, weil nicht verhindert werden kann, dass private Informationen öffentlich werden. Negative Externalitäten bestehen nur, wenn die Informationen zunächst privat bleiben. In beiden Fällen wirkt sich ein Zwang zur Offenlegung negativ auf die Anreize zur Informationsakquisition aus. Allerdings ist dies im ersten Fall aus sozialer Sicht negativ und im zweiten Fall positiv zu beurteilen.
In vielen Fällen ist eine (zumindest partielle) Offenlegung von Informationen unvermeidlich. So muss z.B. beim Handel von Informationen ein Teil vor dem Verkauf preisgegeben werden, um den Käufer vom Nutzen der Informationen zu überzeugen. Legt man aber zu viel offen, wird der Käufer nicht mehr bereit sein, die Information zum geforderten Preis zu erwerben. Der Handel von Informationen ist daher notwendig von Informationsasymmetrie geprägt.
Ebenso führt der Versuch, private Informationsvorteile auszunutzen, auf Märkten häufig dazu, dass ein Teil der Informationen preisgegeben wird. Die Kaufabsicht treibt den Preis nach oben; die Verkaufsabsicht nach unten. Preise aggregieren Informationen und erlauben daher den uninformierten Marktteilnehmern, die private Information der informierten Teilnehmer zu nutzen. Dies reduziert die Anreize, Kosten für die Informationsakquisition aufzubringen. Auf einem Markt, dessen Preise Informationen perfekt widerspiegeln, bestehen deshalb keine Anreize, Informationen zu beschaffen (Grossman, S./Stiglitz, J. 1976). c) Asymmetrische Informationsverteilung
Marktteilnehmer sind nicht nur unvollkommen, sondern häufig auch unterschiedlich gut informiert. Man spricht dann von einer asymmetrischen Informationsverteilung. Ferner ist zu berücksichtigen, dass sie i.d.R. unterschiedliche Interessen verfolgen und mithin Anreize haben, private Informationen zurückzuhalten und Informationsdefizite anderer Teilnehmer auszunutzen.
So wird der Verkäufer eines Gebrauchtwagens besser über die Qualität informiert sein als ein potenzieller Käufer und gleichzeitig Anreize haben, eventuelle Mängel des Wagens zu verschweigen. Ein Versicherungsnehmer wird besser über seine Schadensvorsorge informiert sein als das Versicherungsunternehmen sowie Anreize haben, die Unterlassung von solchen Maßnahmen zu verheimlichen. In beiden Fällen besteht das Problem darin, dass ein Angebot, das aufgrund des Informationsdefizits der einen Partei nur die durchschnittliche Qualität bzw. Schadensvorsorge widerspiegelt, Verhaltensanreize zur Folge hat. Ein Kaufangebot, welches sich an der durchschnittlichen Qualität am Markt orientiert, werden nur Verkäufer mit Gebrauchtwagen unterdurchschnittlicher Qualität annehmen. Dieses Problem wird als „ adverse selection “ bezeichnet. Eine Versicherungsprämie, die sich an der durchschnittlichen und nicht der tatsächlichen Schadensvorsorge orientiert, gibt Anreize, Vorsorgemaßnahmen zu unterlassen, wenn die Versicherung für alle Schäden aufkommt. Dieses Problem bezeichnet man als „ moral hazard “ . Beide Probleme sowie institutionelle Arrangements zur Verringerung der Reibungsverluste aufgrund asymmetrischer Information werden in den Beiträgen Agency-Theorie und Transaktionskosten ausführlich behandelt.
Literatur:
Arrow, Kenneth : Economic Welfare and the Allocation of Resources for Invention, in: The Rate and Direction of Inventive Activity: Economic and Social Factors, hrsg. v. National Bureau of Economic Research, , Princeton 1962, S. 609 – 626
Blackwell, David : Equivalent Comparison of Experiments, in: Annals of Mathematical Statistics, Jg. 24, 1953, S. 265 – 272
Gemünden, Hans Georg : Informationsverhalten, in: HWO, hrsg. v. Frese, Erich, Stuttgart, 3. A., 1992, Sp. 1010 – 1029
Grossman, Sanford/Stiglitz, Joseph : Information and Competitive Price System, in: American Economic Review, Jg. 66, 1976, S. 246 – 253
Hirshleifer, Jack/Riley, John G. : The Analytics of Uncertainty and Information, Cambridge et al. 1992
Laux, Helmut : Entscheidungstheorie, Berlin et al. 1982
Lawrence, David B. : The Economic Value of Information, New York et al. 1999
Maasoumi, Esfandiar : Information Theory, in: The New Palgrave: A Dictionary of Economics, hrsg. v. Eatwell, John/Milgate, Murray/Newman, Peter, London et al. 1987, S. 846 – 850
Mag, Wolfgang : Entscheidung und Information, München 1977
Marschak, Jacob : Economic Information, Decision, Precision, Boston 1974
Marschak, Jacob : Towards an Economic Theory of Organization and Information, in: Decision Processes, hrsg. v. Thrall, Robert M./Coombs, Clyde H./Davis, R.L., New York et al. 1954, S. 187 – 220
Nermuth, Manfred : Information Structures in Economics, Berlin et al. 1982
Shannon, Claude/Weaver, Warren : The Mathematical Theory of Communication, Urbana/IL 1949
Stigler, George J. : The Economics of Information, in: Journal of Political Economy, Jg. 69, 1961, S. 213 – 225
Stiglitz, Joseph : Information and Economic Analysis, in: The Economic Journal, Jg. 95, Supplement/1985, S. 21 – 41
van der Lubbe, Jan C. : Information Theory, Cambridge 1997
Witte, Eberhard : Das Informationsverhalten in Entscheidungsprozessen, in: Das Informationsverhalten in Entscheidungsprozessen, hrsg. v. Witte, Eberhard, Tübingen 1972, S. 1 – 88
Wittmann, Waldemar : Unternehmung und unvollkommene Information, Köln et al. 1959
|