|
Insolvenzgefährdung, Früherkennung
Inhaltsübersicht
I. Ziel der Insolvenzanalyse
II. Probleme der traditionellen Analyse zur Insolvenzfrüherkennung
III. Moderne Verfahren zur Insolvenzfrüherkennung
IV. Möglichkeiten zur Messung der Güte von Systemen zur Insolvenzfrüherkennung
V. Ermittlung von Insolvenzwahrscheinlichkeiten
VI. Einsatzmöglichkeiten und Grenzen von Systemen zur Insolvenzfrüherkennung
I. Ziel der Insolvenzanalyse
Die Insolvenzanalyse dient dazu, möglichst frühzeitig zu erkennen, ob ein Unternehmen insolvenz- bzw. bestandsgefährdet ist oder nicht. Vor allem sind Fremdkapitalgeber an einer Insolvenzanalyse interessiert. Vom Ergebnis dieser Analyse hängt ab, ob sie dem betreffenden Unternehmen einen Kredit gewähren oder nicht und wie sie die Preise dafür gestalten. Auch Lieferanten und Kunden interessieren sich dafür, wie bestandsfest oder bestandsgefährdet das Unternehmen ist, das sie beliefern bzw. dessen Leistungen sie in Anspruch nehmen – Lieferanten, da sie gegenüber dem Unternehmen eine Gläubigerstellung einnehmen – Kunden, wenn langfristige Lieferbeziehungen angestrebt werden und Gewährleistungspflichten zu erfüllen sind. Auch für Wirtschaftsprüfer (WP) ist eine Insolvenzanalyse insbesondere vor dem Hintergrund der Pflichten nach dem KonTraG von großer Bedeutung. Weitere Interessenten sind Gesellschafter, Unternehmensleitung, Beteiligungscontroller und Arbeitnehmer (Baetge, J. 1998a).
Hinweise auf eine Insolvenzgefahr gibt die wirtschaftliche Lage des Unternehmens. Die wirtschaftliche Lage eines Unternehmens lässt sich z.B. aus qualitativen Faktoren wie der Managementqualität, der Branchenentwicklung, der Entwicklung der Absatzmärkte und dem Jahresabschluss ableiten. Dem Jahresabschluss kommt bei der Beurteilung der wirtschaftlichen Lage eine zentrale Bedeutung zu, da er für viele Interessengruppen das einzige verfügbare Informationsinstrument ist und er zudem nach einheitlichen – wenn auch auslegbaren – Grundsätzen ordnungsmäßiger Buchführung aufgestellt wird.
Mit Hilfe der Jahresabschlussanalyse, auch Bilanzanalyse genannt, soll ein Gesamturteil über die wirtschaftliche Lage des analysierten Unternehmens getroffen werden. Bei der Insolvenzanalyse wird aus diesem Gesamturteil abgeleitet, wie hoch die Insolvenzgefährdung des analysierten Unternehmens ist. Dies geschieht durch Angabe einer Insolvenzwahrscheinlichkeit für das analysierte Unternehmen. Je nachdem, ob diese über oder unter dem Durchschnitt in Deutschland liegt, kann die Aussage getroffen werden, dass das analysierte Unternehmen eine über- oder unterdurchschnittliche Insolvenzgefährdung aufweist.
II. Probleme der traditionellen Analyse zur Insolvenzfrüherkennung
Die wirtschaftliche Lage eines Unternehmens, die bei der Insolvenzanalyse untersucht werden muss, setzt sich aus den drei Teillagen Vermögenslage; Finanzlage und Ertragslage zusammen (Leffson, 1984). Jede dieser Lagen ist in verschiedene Informationsbereiche gegliedert, z.B. gehören zur Vermögenslage die Informationsbereiche Kapitalbindung und Kapitalstruktur. Für jeden Informationsbereich können mit verschiedenen Kennzahlen die Informationen des Jahresabschlusses auf einer ersten Aggregationsstufe verdichtet werden. Jede Kennzahl gibt einen bestimmten Sachverhalt komprimiert wieder (Staehle, 1969). Bei der Kennzahlenbildung sollten einige Grundsätze beachtet werden:
| (a) | Es sollten nur Verhältniszahlen gebildet werden. | | (b) | Für jede Kennzahl sollte eine Arbeitshypothese gebildet werden können (Insolvente > Solvente oder Insolvente < Solvente), d.h. Bildung einer Hypothese, ob diese Kennzahl durchschnittlich bei insolventen Unternehmen größer ausfällt als bei solventen oder umgekehrt. | | (c) | Der Nenner einer Kennzahl sollte nicht Null werden können. | | (d) | Zähler und Nenner einer Kennzahl sollten nicht gleichzeitig negativ werden können. | | (e) | Die Kennzahlen sollten betriebswirtschaftlich plausibel sein. |
Bei der traditionellen Analyse zur Insolvenzfrüherkennung hat der Analytiker die Aufgabe, die für die Insolvenzfrüherkennung relevanten Kennzahlen auszuwählen, diese Kennzahlen zu gewichten und so zu einem Gesamturteil zusammenzufassen, dass das Ziel der Insolvenzanalyse, eine zuverlässige Insolvenzfrüherkennung, möglichst gut erreicht wird. Dabei ist der Analytiker auf seine subjektiven Erfahrungen angewiesen. Mit einer subjektiven Kennzahlenauswahl ist indes weder sichergestellt, dass gerade die für die Insolvenzfrüherkennung relevanten Kennzahlen noch dass alle relevanten Kennzahlen herangezogen werden, d.h. es ist nicht gewährleistet, dass das Ganzheitlichkeitsprinzip befolgt wird (Baetge, J. 1998a). Das Ganzheitlichkeitsprinzip sollte bei der Analyse zur Insolvenzfrüherkennung indes immer befolgt werden, damit alle wesentlichen Informationen beachtet werden, so dass die Qualität des Gesamturteils nicht gemindert wird.
Eine ganzheitliche Kennzahlenauswahl unterstützt auch das Neutralisierungsprinzip (Baetge, J. 1998a), das besagt, dass die Kennzahlen so gewählt und verdichtet werden sollten, dass das Gesamturteil von wahrgenommenen Ausweiswahlrechten, Sachverhaltsgestaltungen und bilanzpolitischen Maßnahmen unbeeinflusst ist. Dies kann zum einen dadurch erreicht werden, dass die Kennzahlen ganzheitlich ausgewählt werden, da in diesem Fall eine bilanzpolitische Maßnahme neben der vom Bilanzierenden gewünschten Kennzahl evtl. auch weitere Kennzahlen gegenläufig beeinflussen wird. Der vom Bilanzierenden gewünschte Effekt auf das Gesamturteil könnte somit aufgehoben bzw. neutralisiert werden. Zum anderen wird dem Neutralisierungsprinzip Genüge getan, wenn „ intelligente “ Kennzahlen gebildet werden, die jene Unternehmen, die Wahlrechte unterschiedlich ausüben, gleiche Sachverhalte unterschiedlich gestalten oder bilanzpolitische Maßnahmen getroffen haben, vergleichbar machen, d.h. die jeweiligen Maßnahmen neutralisieren. Allerdings sollten nur jene „ intelligenten “ Kennzahlen herangezogen werden, die genau die Ausweiswahlrechte, Sachverhaltsgestaltungen und bilanzpolitischen Maßnahmen neutralisieren, die von den Unternehmen wahrgenommen werden und die somit einen wirklichen Vorteil für die Urteilsbildung gegenüber herkömmlichen Kennzahlen bedeuten.
Das Objektivierungsprinzip gewährleistet, dass nur die für die Beurteilung der wirtschaftlichen Lage relevanten Kennzahlen zur Gesamturteilsbildung herangezogen werden (Baetge, J. 1998a). Dies bedeutet, dass die Kennzahlen so ausgewählt und zusammengefasst werden, dass eine Falschbeurteilung äußerst selten vorkommt. Anhand von Beispielfällen von sehr vielen Jahresabschlüssen solventer und später insolvent gewordener Unternehmen wird dies empirisch mit Hilfe von statistischen Verfahren und Verfahren der Künstlichen Intelligenz trainiert und gemessen. Zum einen wird das Gesamturteil über die Insolvenzgefährdung eines Unternehmens so intersubjektiv nachprüfbar, d.h. verschiedene Analytiker kommen mit dieser Methode zu dem gleichen Urteil über ein Unternehmen. Zum anderen kann empirisch nachweisbar eine Minimierung von Fehlurteilen gewährleistet werden. Würden dagegen nur subjektive Erfahrungen bei der Auswahl und Gewichtung der Kennzahlen verwendet, könnte dasselbe Unternehmen von verschiedenen Analytikern unterschiedlich beurteilt werden. Dies tritt insbesondere dann auf, wenn der Analytiker einzelne Kennzahlenwerte zusammenfassen muss, wobei einige Kennzahlenwerte das Unternehmen als solvent und andere Kennzahlenwerte das Unternehmen als insolvenzgefährdet darstellen.
Die dargestellten Schwierigkeiten bei der Kennzahlenauswahl, -gewichtung und -zusammenfassung treten nicht nur bei der traditionellen Analyse zur Insolvenzfrüherkennung, sondern auch bei so genannten Scoring-Verfahren auf. Bei einem Scoring-Modell zur Unternehmensbeurteilung, das hier als Nutzwertanalyse oder Punktbewertungsmodell verstanden wird (Adam, 1996), müssen in einem ersten Schritt die zu verwendenden Kennzahlen und deren Gewichtung durch die Ersteller des Modells, bei denen es sich oft um eine Expertengruppe handelt, anhand subjektiver Erfahrungen bestimmt werden. Kennzahlen sind metrisch skalierbar und können direkt in einen Beurteilungsindex eingehen. Beim Scoring werden die möglichen Kennzahlenausprägungen i.d.R. in bestimmte Intervalle aufgeteilt, und diesen werden Punktwerte bzw. Nutzenwerte zugewiesen, die wiederum subjektiv bestimmt werden. Dadurch wird das Gesamturteil noch subjektiver und es gehen Informationen verloren. Scoring-Verfahren haben indes gegenüber der traditionellen Vorgehensweise den Vorteil, dass mit einem einmal erstellten Scoring-Modell jeder Analytiker dem gleichen Unternehmen auch die gleiche Insolvenzgefährdung zuweist und die Urteilsfindung daher intersubjektiv nachprüfbar ist. Das Gesamturteil ist allerdings nicht objektiv richtig (Weber, M./Krahnen, /Weber, A. 1995), sondern nur quasi-objektiv, da die Kennzahlen, wie auch bei der traditionellen Insolvenzanalyse subjektiv ausgewählt, gewichtet und zusammengefasst werden. Mit modernen Verfahren der Insolvenzanalyse wie der Multivariaten Diskriminanzanalyse und der Künstlichen Neuronalen Netzanalyse ist hingegen eine Gesamturteilsbildung möglich, die dem Ganzheitlichkeitsprinzip, dem Neutralisierungsprinzip und dem Objektivierungsprinzip entspricht.
III. Moderne Verfahren zur Insolvenzfrüherkennung
1. Multivariate Diskriminanzanalyse
Mit der linearen Multivariaten Diskriminanzanalyse kann analysiert werden, welche Variablen besonders gut dazu geeignet sind, bestimmte Gruppen zu unterscheiden (Backhaus, /Erichson, /Plinke, et al.1996). Für den Fall der Insolvenzfrüherkennung von Unternehmen kann mit der linearen Multivariaten Diskriminanzanalyse ermittelt werden, welche Kennzahlen besonders zur Trennung solventer und insolvenzgefährdeter Unternehmen geeignet sind. Multivariat bedeutet, dass die Gruppen anhand von mehreren Variablen bzw. Kennzahlen getrennt werden. Die Multivariate Diskriminanzanalyse läuft in drei Schritten ab:
| 1. | Ermittlung der Diskriminanzfunktion; | | 2. | Festlegung des Trennwerts; | | 3. | Prüfung der Klassifikationsleistung der Funktion. |
Im ersten Schritt der Multivariaten Diskriminanzanalyse werden die Kennzahlen ausgewählt, in einer Diskriminanzfunktion gewichtet und linear zusammengefasst:

Dies kann z.B. mit dem Verfahren der schrittweisen Diskriminanzanalyse geschehen. Dazu wird zuerst die Kennzahl in die Diskriminanzfunktion aufgenommen, deren Ausprägungen in den für die Untersuchung zur Verfügung stehenden Jahresabschlüssen den größten Unterschied zwischen solventen und insolvenzgefährdeten Unternehmen aufweisen. Danach wird die Kennzahl in die Diskriminanzfunktion gewählt, die zusammen mit der bereits ausgesuchten Kennzahl solvente und insolvenzgefährdete Unternehmen am besten trennt. Dies wird fortgeführt, bis keine signifikante Verbesserung mehr erreicht werden kann, wenn eine neue Kennzahl aufgenommen wird.
Im Idealfall sollten die relevanten Kennzahlen anhand einer großen Menge von Jahresabschlüssen bzw. zugehörigen Kennzahlenwerten solventer und Jahre später insolvent gewordener Unternehmen aus einem großen, auch „ intelligente “ Kennzahlen umfassenden Kennzahlenkatalog optimal ausgewählt und gewichtet werden, so dass das Neutralisierungsprinzip, das Ganzheitlichkeitsprinzip und das Objektivierungsprinzip befolgt werden können.
Für solche empirischen Analysen muss ein Kriterium bestimmt werden, anhand dessen die Insolvenz erkannt werden kann, d.h. festgestellt werden kann, ob ein empirischer Datensatz als zu einem insolventen Unternehmen gehörig bezeichnet werden kann. Dabei kann kaum auf die gesetzlichen Kriterien wie Überschuldung oder Zahlungsunfähigkeit zurückgegriffen werden, da diese Information i.d.R. nicht vorliegt. Daher sind für jedes Unternehmen bekannte andere, möglichst objektive Kriterien heranzuziehen, wie die juristischen Kriterien Konkurs, Moratorium oder Scheck- bzw. Wechselprotest, die oft im Zusammenhang mit der Überschuldung oder Zahlungsunfähigkeit stehen.
Die zur Verfügung stehenden Daten werden für die Multivariate Diskriminanzanalyse in eine Analysestichprobe und eine Kontrollstichprobe aufgeteilt. Die Analysestichprobe dient der Ermittlung der Diskriminanzfunktion. Anhand der Kontrollstichprobe wird im dritten Schritt der Multivariaten Diskriminanzanalyse die Klassifikationsleistung der Diskriminanzfunktion geprüft. Im zweiten Schritt der Multivariaten Diskriminanzanalyse wird ein kritischer Diskriminanzwert für die Trennung in solvente und insolvenzgefährdete Unternehmen bestimmt. Dieser Trennwert teilt die Skala der Diskriminanzwerte (D-Werte = Rating-Urteile). Alle Unternehmen mit einem D-Wert über dem Trennwert werden als „ solvent “ und alle Unternehmen mit einem D-Wert unter dem Trennwert werden als „ insolvenzgefährdet “ klassifiziert (oder umgekehrt, je nach Transformation der Skala). Von der Wahl des Trennwerts hängt ab, wie viele Unternehmen falsch klassifiziert werden. Die Wahl des Trennwerts lässt sich anhand von ökonomischen Kriterien, z.B. Fehlerkosten und Beurteilungskosten, optimieren.
2. Künstliche Neuronale Netzanalyse a) Informationsverarbeitung in einem Künstlichen Neuronalen Netz
Ein Künstliches Neuronales Netz besteht ähnlich einem biologischen neuronalen Netz (z.B. dem menschlichen Gehirn) aus miteinander verbundenen Zellen, den so genannten Neuronen (Rojas, 1996). Die Neuronen eines Künstlichen Neuronalen Netzes sind meist in Schichten angeordnet. Die Neuronen aufeinander folgender Schichten sind miteinander verbunden (vgl. Abb. 1). Die Neuronen der Eingabeschicht nehmen Informationen in das Netz auf, die Neuronen der versteckten Schicht(en) verarbeiten die Informationen für den Anwender unsichtbar im Netzinnern. Von dort werden sie an das (die) Neuron(en) der Ausgabeschicht geleitet. In der Ausgabeschicht wird die Netzausgabe berechnet und an die Außenwelt gegeben (Zell, 1996).
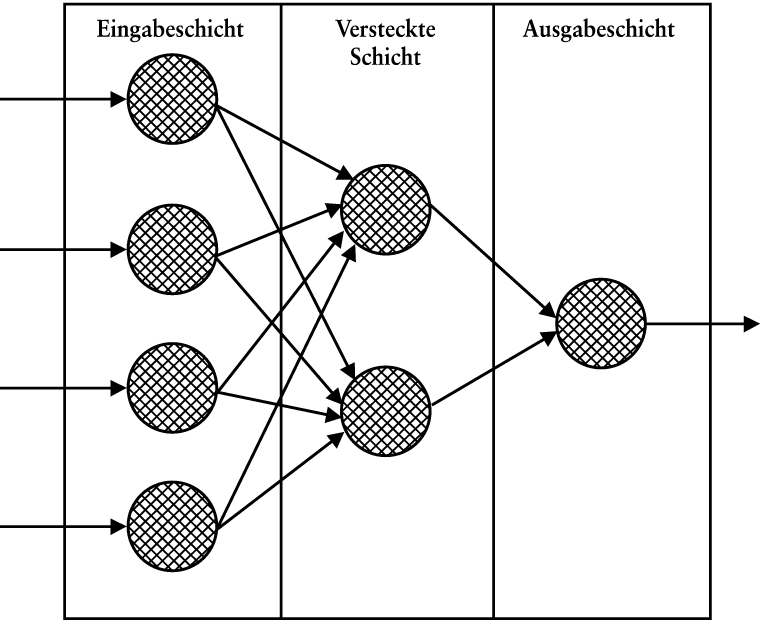
Abb. 1: Struktur eines Künstlichen Neuronalen Netzes
Die Verbindungen zwischen den Neuronen aufeinander folgender Schichten repräsentieren Gewichte. Die Eingabe in ein künstliches Neuron wird meist als die Summe aus den mit den Verbindungsgewichten multiplizierten Ausgaben der Vorgängerneuronen berechnet (Propagierungsfunktion). Bei Neuronen der Eingabeschicht wird die von außen erfolgende Netzeingabe direkt, i.d.R. noch transformiert, übernommen.
Die Aktivierung des Neurons wird aus der Eingabe mit Hilfe einer Aktivierungsfunktion berechnet. Mögliche Aktivierungsfunktionen sind die sigmoiden, d.h. s-förmigen Funktionen, die logistische Funktion und der Tangens hyperbolicus, mit denen der Einfluss von Ausreißern gemildert wird. Weitere Aktivierungsfunktionen sind die lineare Funktion und die Schwellwertfunktion, bei der die Eingabe in das Neuron einen bestimmten Schwellwert überschreiten muss, damit ein Aktivierungszustand ungleich Null erreicht wird.
Die Ausgabe des Neurons wird mittels einer Ausgabefunktion (i.d.R. die Identitätsfunktion) aus der Aktivierung des Neurons berechnet. Aus den Ausgaben dieses Neurons, der weiteren Neuronen der gleichen Schicht und ihren jeweiligen Verbindungsgewichten zu den Neuronen der nachfolgenden Schicht werden wieder die Eingaben in die Neuronen der nachfolgenden Schicht berechnet. Diese Informationsverarbeitung setzt sich bis zu den Neuronen der Ausgabeschicht fort. In Abb. 2 ist die Informationsverarbeitung in einem künstlichen Neuron schematisch dargestellt.
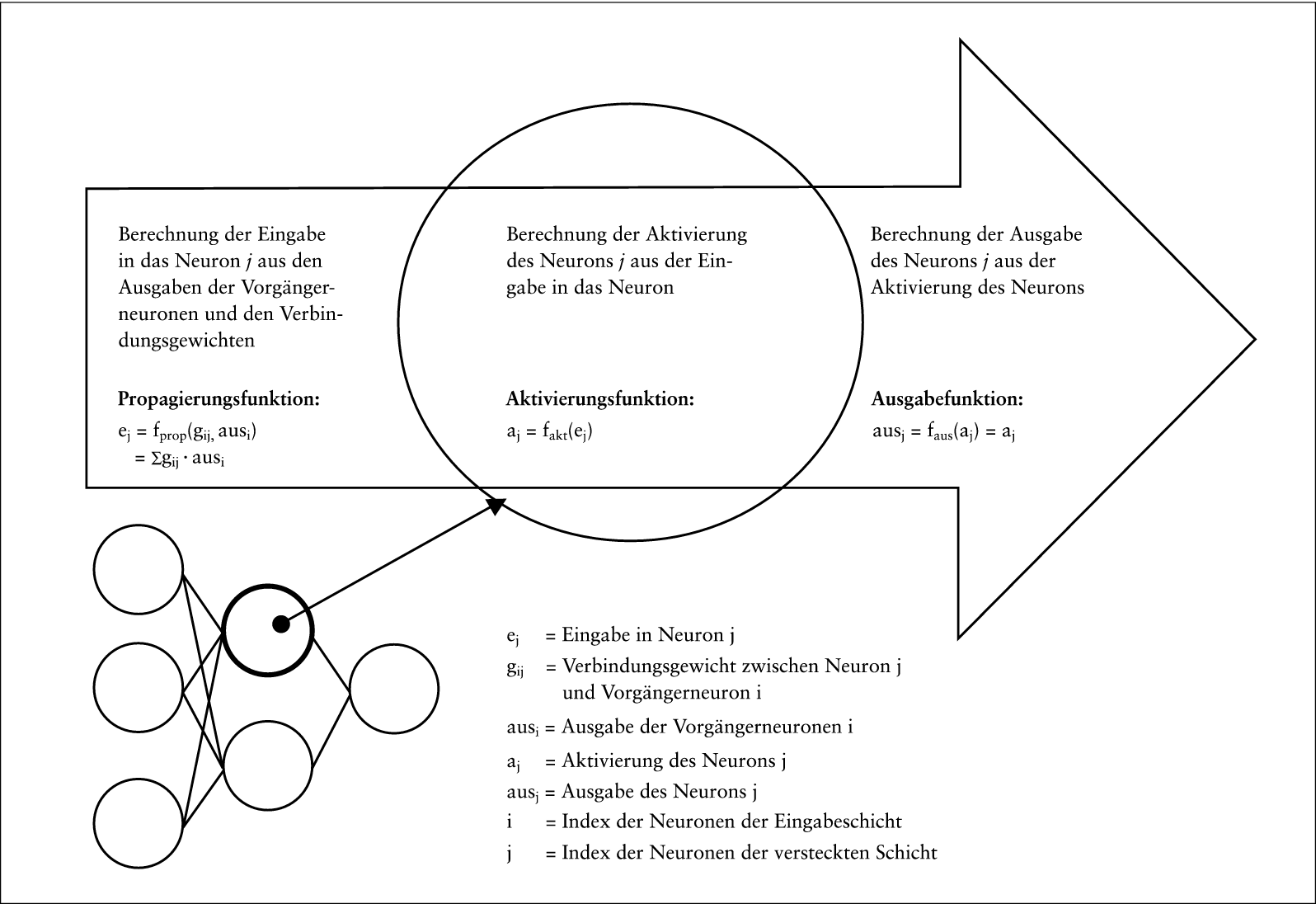
Abb. 2: Informationsverarbeitung in einem künstlichen Neuron
Die Netzausgabe (der N-Wert) resultiert aus einer Kette von Funktionen, deren Variablen die Netzeingaben und die Verbindungsgewichte sind. Die Netzeingaben sind für den Fall der Insolvenzanalyse i.d.R. Jahresabschlusskennzahlen. Diese Kennzahlen werden, wie oben beschrieben, durch das Netz bis zur Netzausgabe, dem Gesamturteil über das Unternehmen, verarbeitet. Die Verbindungsgewichte müssen dabei so gewählt werden, dass das Gesamturteil möglichst zutrifft. Der optimale Gewichtsvektor kann bei der Künstlichen Neuronalen Netzanalyse über so genannte Lernalgorithmen gefunden werden, mit denen die Verbindungsgewichte nach und nach angepasst werden (Zell, 1996). Wie schon bei der Multivariaten Diskriminanzanalyse sollte auch ein Künstliches Neuronales Netz an möglichst vielen Beispieldatensätzen, d.h. Kennzahlenvektoren solventer und später insolventer Unternehmen, lernen. Ein besonders zur Lösung von Klassifikationsproblemen geeigneter Lernalgorithmus ist der Backpropagation-Algorithmus (Krause, 1993). Mit diesem Algorithmus wird zunächst für einen Beispieldatensatz die Netzausgabe, d.h. das Urteil des Netzes, ob das Unternehmen solvent oder insolvenzgefährdet ist, berechnet. Diese Ist-Ausgabe wird dann mit der Soll-Ausgabe verglichen, nämlich mit der Information, ob es sich tatsächlich um ein solventes oder ein später insolventes Unternehmen handelt (kodiert z.B. mit 0 und 1). Anschließend werden die Verbindungsgewichte rückwärts gerichtet (backpropagation) durch das Netz so angepasst, dass die Abweichung zwischen Soll-Ausgabe und Ist-Ausgabe (Netzfehler) minimiert wird (Rumelhart, /Hinton, /Williams, 1986). So wird mit jedem Beispieldatensatz verfahren. Die Verbindungsgewichte können nach jeder Berechnung eines vorläufigen Ausgabewerts für jeden Beispieldatensatz angepasst werden (Onlineverfahren) oder einmal nach allen Datensätzen (Offline- oder Batch-Verfahren) (Zell, 1996). Mit der Künstlichen Neuronalen Netzanalyse ist eine nicht-lineare Trennung zwischen solventen und insolvenzgefährdeten Unternehmen möglich. Damit können die Ergebnisse der multivariaten linearen Klassifikation noch verbessert werden. b) Stichprobenaufteilung bei der Künstlichen Neuronalen Netzanalyse
Die Datensätze für die Entwicklung eines Künstlichen Neuronalen Netzes müssen statt wie bei der Multivariaten Diskriminanzanalyse auf zwei bei der Künstlichen Neuronalen Netzanalyse auf drei Stichproben aufgeteilt werden: die Analysestichprobe, die Teststichprobe und die Validierungsstichprobe. An den Datensätzen der Analysestichprobe lernt das Netz. Sie werden dem Netz immer wieder präsentiert, damit seine Verbindungsgewichte optimal eingestellt werden können. Das Netz darf die Strukturen der Analysestichprobe aber nicht „ auswendig “ lernen, damit es seine Generalisierungsfähigkeit, d.h. die Fähigkeit, auch fremde Datensätze sicher zu beurteilen, nicht verliert. Dieses so genannte overlearning oder overtraining muss verhindert werden, da das Netz bei der praktischen Anwendung Unternehmen beurteilen soll, deren Jahresabschlüsse nicht für die Entwicklung verwendet wurden. Dafür wird die Methode des stopped-training angewendet, wobei die Klassifikationsleistung des Netzes während der Entwicklung ständig auch an den Datensätzen der Teststichprobe geprüft wird. Diese Datensätze werden nicht zum Lernen verwendet. Wenn der Klassifikationsfehler des Netzes an der Teststichprobe sein Minimum erreicht hat (bei Zopt in Abb. 3), wird das Netztraining abgebrochen, auch wenn der Klassifikationsfehler an der Analysestichprobe weiter sinkt, wie in Abb. 3 zu sehen ist (Zimmermann, H. G. 1994).
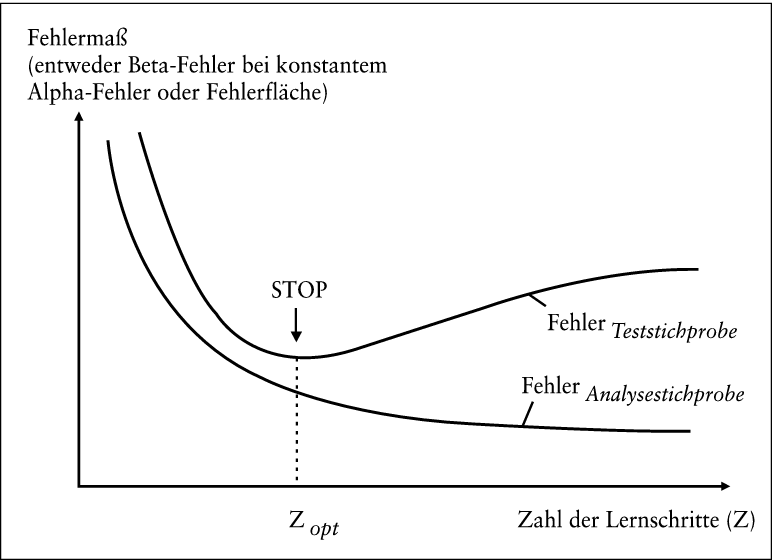
Abb. 3: stopped-training
Die Teststichprobe wird außerdem benötigt, um die für die Insolvenzanalyse relevanten Kennzahlen auszuwählen. Vor der Künstlichen Neuronalen Netzanalyse wird ein großer Katalog betriebswirtschaftlich plausibler Kennzahlen gebildet. Da aufgrund ihrer großen Zahl nicht sämtliche Kennzahlenkombinationen getestet werden können, werden zur Kennzahlenauswahl Heuristiken angewendet, sog. Pruning- und Insertion-Verfahren. Beim Pruning sind das gewichtsorientierte und das relevanzorientierte Pruning zu unterscheiden (Uthoff, 1997). Beim gewichtsorientierten Pruning werden die Neuronenverbindungen mit den kleinsten Gewichten „ abgeschnitten “ . Dahinter steht die Vermutung, dass kleine Verbindungsgewichte nur einen geringen Einfluss auf die Klassifikationsleistung des Netzes haben. Beim relevanzorientierten Pruning werden Neuronen mit einer negativen Relevanz (Relevanz = Differenz der Netzfehler mit und ohne das betreffende Neuron, gemessen an der Teststichprobe) entfernt, d.h. alle Verbindungen dieses Neurons werden getrennt. Beim Insertion-Verfahren werden ausgehend von einem Netz mit wenigen in Voranalysen als wichtig identifizierten Kennzahlen weitere Kennzahlen hinzugefügt, wenn die Klassifikationsleistung des Netzes an der Teststichprobe mit der jeweiligen Kennzahl besser ist als ohne die Kennzahl.
Die Klassifikationsleistung des fertig entwickelten Netzes ist abschließend an den bisher nicht verwendeten Datensätzen der Validierungsstichprobe zu prüfen. Die Datensätze der Validierungsstichprobe sind dem Netz genauso fremd wie die Unternehmen, die es in der praktischen Anwendung beurteilen soll. Nur so kann die Klassifikationsleistung eines Netzes objektiv gemessen werden. Schließlich wird anhand der Validierungsstichprobe das beste Künstliche Neuronale Netz ausgewählt und der Anwendung bei der Insolvenzanalyse zugrunde gelegt. Da das Netz bei der Anwendung praktischer Fälle nicht mehr weiter lernt, spricht man hier von einem geronnenen Netz.
IV. Möglichkeiten zur Messung der Güte von Systemen zur Insolvenzfrüherkennung
Die Klassifikationsleistung eines Systems zur Insolvenzfrüherkennung, z.B. einer Multivariaten Diskriminanzfunktion oder eines Künstlichen Neuronalen Netzes, wird daran gemessen, wie viele Unternehmen das System falsch beurteilt. Das System kann zum einen einen so genannten Alpha-Fehler begehen. Der Alpha-Fehler ist der Anteil der fälschlich als „ solvent “ klassifizierten, tatsächlich später insolventen Unternehmen an allen später insolventen Unternehmen. Zum anderen kann das System einen so genannten Beta-Fehler begehen. Der Beta-Fehler ist der Anteil der fälschlich als „ insolvenzgefährdet “ klassifizierten, tatsächlich solventen Unternehmen an allen solventen Unternehmen. Der Trennwert ist der Wert auf der Skala des Gesamturteils, der als „ solvent “ beurteilte Unternehmen von als „ insolvenzgefährdet “ beurteilten Unternehmen trennt. Sind z.B. hohe Gesamturteilswerte gut und niedrige schlecht zu beurteilen, werden alle Unternehmen mit einem Gesamturteil über dem Trennwert als „ solvent “ und alle Unternehmen mit einem Gesamturteil unter dem Trennwert als „ insolvenzgefährdet “ klassifiziert. Da Alpha- und Beta-Fehler vom gewählten Trennwert abhängig sind, sind mit einem System zur Insolvenzfrüherkennung so viele verschiedene Alpha-Beta-Fehlerkombinationen wie Trennwerte möglich. Beide Fehler stehen in einem Austauschverhältnis zueinander, d.h. eine Verminderung des einen Fehlers durch eine Verschiebung des Trennwerts hat immer eine Erhöhung des anderen Fehlers zur Folge.
In der linken Grafik sind in Abb. 4 die Dichtefunktionen der Gesamturteilswerte der solventen und der später insolventen Unternehmen, wie sie mit einem Künstlichen Neuronalen Netz errechnet worden sein könnten, mit einem Trennwert NT und dem sich aus diesem Trennwert ergebenden Alpha-Fehler und Beta-Fehler dargestellt.
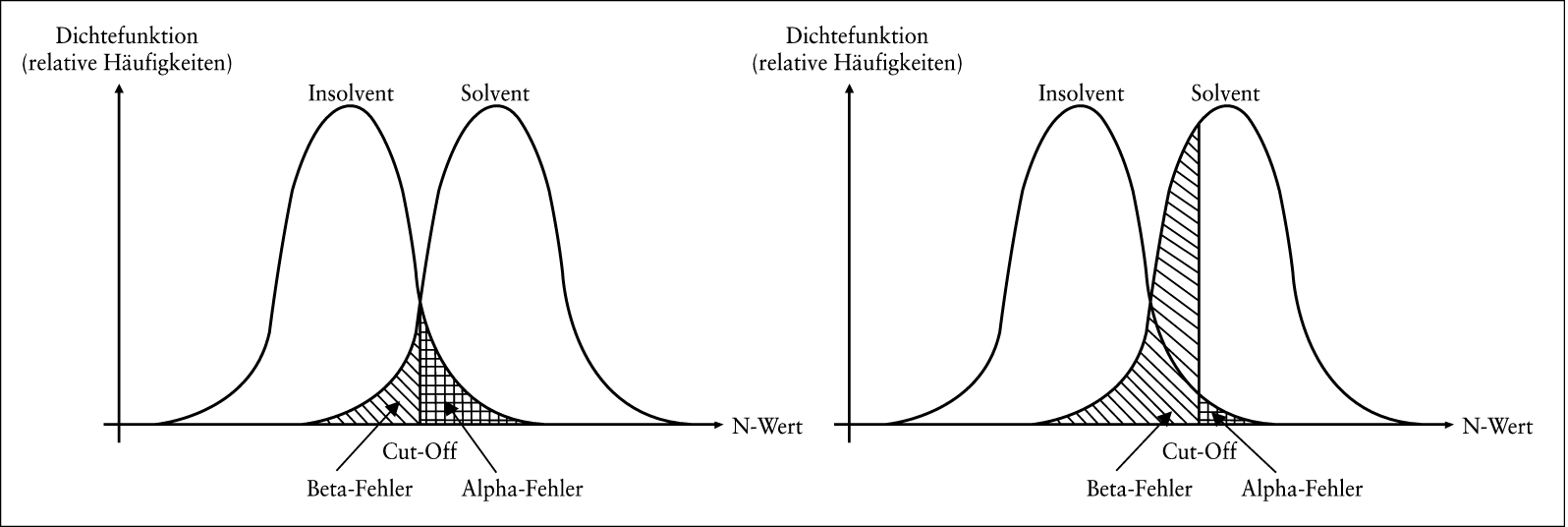
Abb. 4: Dichtefunktionen der solventen und insolventen Unternehmen
In der rechten Grafik in Abb. 4 ist zu sehen, dass sich der Alpha-Fehler verringert und der Beta-Fehler erhöht, wenn der Trennwert in Richtung höherer Gesamturteilswerte verschoben wird. Wird der Trennwert in Richtung niedrigerer Gesamturteilswerte verschoben, erhöht sich der Alpha-Fehler und verringert sich der Beta-Fehler.
Alle Alpha-Beta-Fehlerkombinationen, die bei alternativen Trennwerten mit einem System zur Insolvenzfrüherkennung erreicht werden können, lassen sich mit einer Alpha-Beta-Fehlerfunktion darstellen, wie sie in Abb. 5 zu sehen ist. An der Abszisse des Koordinatensystems für die Alpha-Beta-Fehlerfunktion ist der Alpha-Fehler abgetragen, an der Ordinate der Beta-Fehler. Die beiden äußersten Punkte der Kurve sind (0%/100%) und (100%/0%). Dazwischen verläuft die Kurve vom Ursprung aus betrachtet i.d.R. konvex. Die Fläche unter dieser Kurve ist die so genannte Fehlerfläche (Uthoff, 1997). Sie ist umso größer, je weiter entfernt die Kurve vom Ursprung ist, und umso geringer, je näher die Alpha-Beta-Fehlerkurve am Ursprung liegt, d.h. je geringere Beta-Fehler über alle Alpha-Fehler bzw. umgekehrt erreicht werden. Die Fehlerfläche lässt sich als durchschnittlicher Beta-Fehler über alle Alpha-Fehler oder als durchschnittlicher Alpha-Fehler über alle Beta-Fehler interpretieren (Jerschensky, 1998). Ein System zur Insolvenzfrüherkennung klassifiziert also durchschnittlich über alle Alpha-Fehler bzw. Beta-Fehler umso besser, je geringer seine Fehlerfläche ist. Abb. 5 zeigt beispielhaft die Alpha-Beta-Fehlerfunktion eines Beurteilungssystems K mit der darunter liegenden Fehlerfläche.
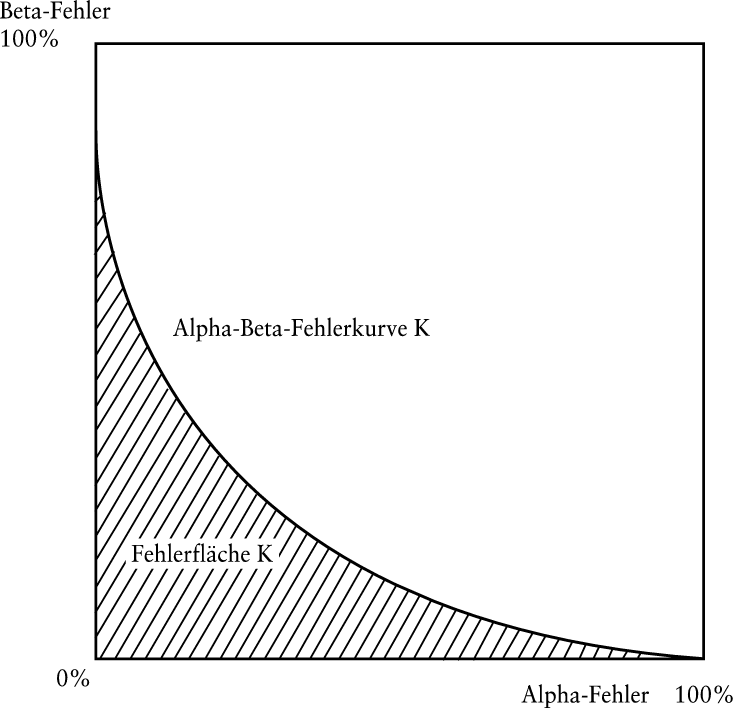
Abb. 5: Alpha-Beta-Fehlerfunktion und Fehlerfläche eines Systems zur Unternehmensbeurteilung K
Ein weiteres Maß für die Klassifikationsleistung eines Systems zur Insolvenzfrüherkennung ist z.B. der Gesamtfehler, d.h. der Prozentsatz aller Fehlklassifikationen. Dieses Fehlermaß hat den Nachteil, dass es vom gewählten Trennwert abhängig ist. Oft wird der Trennwert für die Bestimmung des Gesamtfehlers so gewählt, dass die geringsten Fehlklassifikationen auftreten. Dabei wird indes nicht zwischen Alpha-Fehler und Beta-Fehler differenziert, und somit werden die mit beiden Fehlern verbundenen unterschiedlichen Kosten nicht berücksichtigt. Auch der Beta-Fehler bei einem bestimmten Alpha-Fehler ist ein Maß für die Klassifikationsleistung eines Systems zur Insolvenzfrüherkennung. Auch hier besteht indes der Nachteil, dass das Fehlermaß vom Trennwert abhängt. Das Fehlerflächenkonzept ist daher u.E. das am besten geeignete Maß für die Klassifikationsleistung eines Beurteilungssystems.
V. Ermittlung von Insolvenzwahrscheinlichkeiten
Mit modernen Systemen zur Insolvenzfrüherkennung werden Unternehmen in die beiden Gruppen solvent und insolvenzgefährdet klassifiziert. Indes erlaubt der D-Wert bzw. N-Wert (Bonitätsindex) eines Unternehmens weitergehende Aussagen als nur eine Aussage über diese Gruppenzugehörigkeit. Der Bonitätsindex eines Unternehmens kann nicht nur die zwei Werte solvent oder insolvenzgefährdet annehmen, sondern er kann zwischen dem oberen und dem unteren Ende einer Skala beliebige Werte annehmen. Unternehmen können somit anhand des Bonitätsindexes in eine Rangfolge bzgl. ihrer Bonität gebracht werden. Die Skala des Bonitätsindexes kann in Bonitätsklassen unterteilt und die Unternehmen können anhand ihres Bonitätsindexes den Bonitätsklassen zugeordnet werden. Für jede Bonitätsklasse lässt sich eine Solvenzwahrscheinlichkeit und eine Insolvenzwahrscheinlichkeit für die Unternehmen in dieser Klasse nach dem Bayes-Theorem wie folgt berechnen (Bleymüller, /Gehlert, /Gülicher, 1998):

Die a-posteriori Insolvenzwahrscheinlichkeit einer Klasse gibt also das Risiko an, dass ein Unternehmen in dieser Klasse insolvent wird. Die a-posteriori Solvenzwahrscheinlichkeit ist dazu die Gegenwahrscheinlichkeit. Die a-posteriori Wahrscheinlichkeiten sind von den a-priori Wahrscheinlichkeiten für Solvenz und Insolvenz und von den bedingten Wahrscheinlichkeiten abhängig, dass ein solventes bzw. später insolventes Unternehmen in eine bestimmte Klasse klassifiziert wird.
Die a-priori Wahrscheinlichkeit gibt den Anteil der solventen bzw. später insolventen Unternehmen an allen der Analyse zugrunde liegenden Unternehmen an. Je größer der Anteil der später insolventen Unternehmen an allen Unternehmen ist, desto höher wird das Niveau der a-posteriori Insolvenzwahrscheinlichkeiten in den Bonitätsklassen. Denn je mehr später insolvente Unternehmen klassifiziert werden, desto höher ist ihr Anteil in den Bonitätsklassen.
Indes ist bei einem gut trennenden Klassifikator zu erwarten, dass eher die a-posteriori Insolvenzwahrscheinlichkeiten in den unteren Klassen steigen werden. Ob dies so ist, hängt von den bedingten Wahrscheinlichkeiten ab, dass ein solventes bzw. später insolventes Unternehmen in eine bestimmte Klasse klassifiziert wird. Die bedingten Wahrscheinlichkeiten für die einzelnen Klassen können empirisch ermittelt werden, indem der Anteil der in die jeweilige Klasse klassifizierten solventen bzw. später insolventen Unternehmen an allen solventen bzw. später insolventen Unternehmen berechnet wird. Hierdurch geht die Verteilung des Bonitätsindexes, die ein bestimmter Klassifikator erzeugt, in die Berechnung der a-posteriori Wahrscheinlichkeiten ein. Werden später insolvente Unternehmen eher in die unteren Klassen eingeteilt, sind auch die a-posteriori Insolvenzwahrscheinlichkeiten in den unteren Klassen höher. Werden die bedingten Wahrscheinlichkeiten empirisch ermittelt, ist zu beachten, dass der Anteil der später insolventen Unternehmen an allen zu klassifizierenden Unternehmen der gewünschten a-priori Insolvenzwahrscheinlichkeit entsprechen muss. Ist dies nicht der Fall, da der zur Verfügung stehende Datenbestand anders verteilt ist, sind die Unternehmen in den einzelnen Bonitätsklassen entsprechend zu gewichten.
VI. Einsatzmöglichkeiten und Grenzen von Systemen zur Insolvenzfrüherkennung
Systeme zur Insolvenzfrüherkennung werden vor allem von Kreditinstituten bei der Prüfung von Kreditanträgen eingesetzt. Mit modernen Systemen zur Insolvenzfrüherkennung können im Vergleich zur traditionellen Kreditprüfung erhebliche Kosten eingespart werden. Lässt man z.B. auf einer ersten Stufe der Kreditprüfung ein modernes System zur Insolvenzfrüherkennung alle Kreditanträge vorprüfen und werden auf einer zweiten Stufe nur noch alle als insolvenzgefährdet beurteilten Kunden intensiv durch Kreditsachbearbeiter geprüft, während die vom System als solvent beurteilten Kunden ohne weitere Prüfung oder nur nach einer verkürzten Prüfung angenommen werden, können zum einen Bearbeitungskosten gespart werden. Denn nicht mehr alle Anträge müssen intensiv geprüft werden. Zum anderen können Opportunitätskosten und Ausfallkosten gespart werden, wenn das moderne System zur Insolvenzfrüherkennung eine entsprechende Güte aufweist und somit durch die zuverlässige Vorauswahl in Verbindung mit der gezielten Nachprüfung weniger solvente Kunden fälschlich abgelehnt und weniger insolvente Kunden fälschlich angenommen werden (Baetge, J. 1998b).
Ein weiteres großes Einsatzgebiet von modernen Systemen zur Insolvenzfrüherkennung ist die Wirtschaftsprüfung. Da mit modernen Systemen zur Insolvenzfrüherkennung Fortbestandsrisiken quantifiziert werden können, sind solche Systeme zum einen ein wertvolles Hilfsmittel bei der Realisierung des risikoorientierten Prüfungsansatzes zur Bestimmung des inhärenten Risikos. Zum anderen leisten solche Systeme wertvolle Unterstützung bei der Erfüllung der Pflichten des Wirtschaftsprüfers nach dem Gesetz zur Kontrolle und Transparenz im Unternehmensbereich (KonTraG) (Baetge, J./Baetge, K./Kruse, 1999b).
Wie bereits beschrieben, urteilen moderne Systeme zur Insolvenzfrüherkennung nicht fehlerfrei. Denn wenn ihr Urteil ausschließlich auf Bilanzdaten beruht, werden Informationen außerhalb der Bilanz, die vielleicht die Lage des Unternehmens anders aussehen lassen, nicht berücksichtigt. Aber selbst wenn auch qualitative Informationen berücksichtigt werden, umfassen diese Informationen ein großes Maß an Subjektivität. Denn bevor z.B. Merkmale, wie Managementqualität oder die Aussichten einer Branche, in das Gesamturteil über ein Unternehmen eingehen können, müssen sie beurteilt werden, so dass Subjektivität nicht vermieden werden kann.
Daher sollte sich der Anwender über die Folgen eines Fehlurteils klar werden und den Prozess, in dem das System eingesetzt wird, entsprechend gestalten. Für die Kreditwürdigkeitsprüfung mit modernen Systemen zur Insolvenzfrüherkennung bedeutet dies, dass der Trennwert auf der Skala der Bonitätsurteile so gewählt werden sollte, dass die Kosten des Kreditprüfungsprozesses minimal bzw. der Erfolg maximal wird. Für den Einsatz solcher Systeme in der Wirtschaftsprüfung bedeutet dies, dass ein solches System zwar ein wertvolles Hilfsmittel bei der einheitlichen Gesamturteilsbildung und Quantifizierung des Fortbestandsrisikos ist, der Wirtschaftsprüfer sich aber stets ein eigenes Bild von der Lage machen sollte, wobei er alle ihm zur Verfügung stehenden Informationen heranziehen muss.
Literatur:
Adam, D. : Planung und Entscheidung, 4. A., Wiesbaden 1996
Backhaus, K./Erichson, B./Plinke, W. : Multivariate Analysemethoden, 8. A., Berlin u.a. 1996
Baetge, J. : Bilanzanalyse, Düsseldorf 1998a
Baetge, J. : Stabilität eines Bilanzbonitätsindikators und seine Einsatzmöglichkeiten im Kreditgeschäft, 2. Teil: Zum praktischen Einsatz in der Bonitätsprüfung, in: Der Schweizer Treuhänder, 1998b, S. 751 – 758
Baetge, J./Baetge, K./Kruse, A. : Grundlagen moderner Verfahren der Jahresabschlußanalyse, in: DStR 1999a, S. 1371 – 1376
Baetge, J./Baetge, K./Kruse, A. : Einsatzmöglichkeiten eines modernen Bilanz-Ratings in der Wirtschaftsprüfer- und Steuerberaterpraxis, in: DStR 1999b, S. 1919 – 1924
Bleymüller, J./Gehlert, G./Gülicher, H. : Statistik für Wirtschaftswissenschaftler, 11. A., München 1998
Jerschensky, A. : Messung des Bonitätsrisikos von Unternehmen, Krisendiagnose mit Künstlichen Neuronalen Netzen, Düsseldorf 1998
Krause, C. : Kreditwürdigkeitsprüfung mit Neuronalen Netzen, Düsseldorf 1993
Leffson, U. : Bilanzanalyse, 3. A., Stuttgart 1984
Rojas, R. : Theorie der neuronalen Netze, Eine systematische Einführung, 4. korrigierter Nachdruck, Berlin et al. 1996
Rumelhart, D. E./Hinton, G. E./Williams, R. J. : Learning Internal Representations by Error Propagation, in: Parallel Distributed Processing, Explorations in the Microstructure of Cognition, Volume 1: Foundations, hrsg. v. Rumelhart, D. E./McClelland, J. L./PDP Research Group, , Cambridge, Massachusetts 1986, S. 318 – 362
Staehle, W. H. : Kennzahlen und Kennzahlensysteme als Mittel der Organisation und Führung von Unternehmen, Wiesbaden 1969
Uthoff, C. : Erfolgsoptimale Kreditwürdigkeitsprüfung auf der Basis von Jahresabschlüssen und Wirtschaftsauskünften mit Künstlichen Neuronalen Netzen, Stuttgart 1997
Weber, M./Krahnen, J./Weber, A. : Scoring-Verfahren – häufige Anwendungsfehler und ihre Vermeidung, in: DB 1995, S. 1621 – 1626
Zell, A. : Simulation Neuronaler Netze, 1. unveränderter Nachdruck, Bonn et al. 1996
Zimmermann, H. G. : Neuronale Netze als Enscheidungskalkül, in: Neuronale Netze in der Ökonomie, hrsg. v. Rehkugler, H./Zimmermann, H. G., München 1994, S. 1 – 87
|