|
Kalkulationszinsfuß
Inhaltsübersicht
I. Einführung
II. Kalkulationszinsfuß unter Sicherheit
III. Kalkulationszinsfuß unter Risiko
IV. Kalkulationszinsfuß und Steuern
I. Einführung
Der Kalkulationszinsfuß spielt in dynamischen Investitionsrechenverfahren, sowie bei ertragsorientierter Unternehmensbewertung eine zentrale Rolle. Aus ihm gewinnt man die Diskontfaktoren, welche bei der Ermittlung von Barwerten künftiger Zahlungen eingesetzt werden. Von allen dynamischen Verfahren der Investitionsrechnung besitzt die Kapitalwertmethode die bei weitem größte Akzeptanz. Die Diskussion um die Frage, wie man den Kalkulationszinsfuß bestimmen sollte, wurde in der Literatur jedenfalls konzentriert vor dem Hintergrund genau dieser Methode der Investitionsbeurteilung geführt.
Gewöhnlich weist man bei der Darstellung der Kapitalwertmethode unter Sicherheit darauf hin, dass eine ihrer Anwendungsvoraussetzungen die Existenz eines vollkommenen Kapitalmarktes ist. Seit den frühen 1960er-Jahren weiß man aber, dass die Kapitalwertmethode auch dann benutzt werden kann, wenn der Kapitalmarkt unvollkommen und beschränkt ist.
Wesentliches Kennzeichen eines vollkommenen Kapitalmarktes ist die Identität von Kreditaufnahme- und Geldanlagezinssätzen. Bei Sicherheit gibt es keinen Grund, verschiedene Finanzierungsformen (Kredit- und Beteiligungskapital) zu unterscheiden. Infolgedessen benutzt man als Kalkulationszinsfuß „ den “ Marktzinssatz. Bezeichnen πt den Diskontfaktor für eine Zahlung, die im Zeitpunkt t > 0 fällig ist, und r „ den “ Marktzinssatz, so gilt
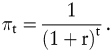
Für praktische Anwendungen ist damit wenig gewonnen, denn es bleibt offen, wie der Kalkulationszinsfuß unter weniger idealen Bedingungen zu wählen ist.
Trivial ist das Thema aber nicht einmal hier, es sei denn man unterstellt, dass „ der “ Marktzins unabhängig von der Laufzeit finanzieller Engagements ist. Alle empirischen Beobachtungen weisen darauf hin, dass das regelmäßig nicht der Fall ist. Unter normalen Umständen sind die Zinssätze für kurze Laufzeiten niedriger als für lange Laufzeiten. Dann aber gibt es mehr als einen Marktzinssatz, und es ist zu fragen, welcher davon die Rolle des Kalkulationszinsfußes übernehmen soll.
Es bietet sich an, das Konzept eines einheitlichen Kalkulationszinsfußes aufzugeben und statt dessen mit mehreren laufzeitabhängigen Zinssätzen zu arbeiten. Je nach Fristigkeit der Cashflows wird mit dem entsprechenden Satz diskontiert. Dabei gibt es die Möglichkeit, entweder auf Umlaufrenditen von Kupon-Anleihen (yields) mit unterschiedlicher Restlaufzeit zurückzugreifen oder die Renditen von Zero Bonds (spot rates) zu benutzen. In der Finanzierungstheorie gilt der zweite Weg als der bessere. Verwendet man r0,t für die Rendite eines Zero Bonds mit t-jähriger Laufzeit, so ergeben sich die Diskontfaktoren aus
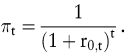
Auf arbitragefreien Kapitalmärkten kommt man zu identischen Ergebnissen, wenn man mit der spot rate für einjährige Kapitalanlagen und einer Folge von einjährigen Terminzinssätzen (forward rates) arbeitet. Steht beispielsweise 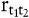 für die forward rate zwischen den Zeitpunkten t1 und t2 mit für die forward rate zwischen den Zeitpunkten t1 und t2 mit 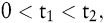 so erhält man die gleichen Diskontfaktoren aus so erhält man die gleichen Diskontfaktoren aus
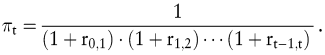
Wegen der Tatsache, dass sowohl die Märkte für Nullkupon-Anleihen verhältnismäßig dünn sind als auch Terminkontrakte des hier angesprochenen Typs insbesondere im langfristigen Bereich nicht gehandelt werden, bietet es sich an, pragmatisch vorzugehen und doch auf Effektivrenditen umlaufender Kupon-Anleihen zurückzugreifen. Man muss nicht unbedingt befürchten, dass die hieraus resultierenden Bewertungsfehler wirklich bedeutend sind.
Bei Entscheidungen über das optimale Kapitalbudget unter Sicherheit geht man, einer Idee Dean, folgend, wie folgt vor: In einem ersten Schritt werden die Investitionsprojekte nach ihren Renditen in fallender Reihenfolge geordnet. In graphischer Darstellung entsteht auf diese Weise eine Kapitalnachfragekurve. Danach sortiert man die verfügbaren Finanzierungsmaßnahmen nach ihren Kapitalkosten in steigender Reihenfolge. Auf diese Weise erhält man eine Kapitalangebotskurve. Der Schnittpunkt beider Kurven markiert auf der Abszisse das optimale Kapitalbudget und auf der Ordinate einen Zinssatz, den man als endogenen Kalkulationszinsfuß oder als cut off rate bezeichnet. Dieser Zinssatz hat eine bemerkenswerte Eigenschaft. Wenn man ihn kennt, kann man das optimale Kapitalbudget mit Hilfe der Kapitalwertmethode bestimmen. Alle Projekte, deren Realisierung sich lohnt, haben einen nicht-negativen Kapitalwert, falls man die cut off rate als Kalkulationszinsfuß verwendet. Leider kennt man die cut off rate erst, wenn man das Planungsproblem bereits gelöst hat.
Inzwischen weiß man, dass mit Hilfe des oben angegebenen Rangordnungsverfahrens nicht immer die optimale Lösung gefunden wird. Wir wissen weiter, dass sich mit Hilfe von Verfahren der Linearen Programmierung das die Zielfunktion des Investors maximierende Kapitalbudget exakt ermitteln lässt. Ferner wissen wir, dass sich aus den Dualwerten des Lösungstableaus auch wieder endogene Kalkulationszinsfüße ableiten lassen. Bezeichnet dt den Dualwert für die Liquiditätsnebenbedingung des Zeitpunktes t, so erhält man geeignete Diskontfaktoren aus
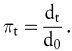
Wenn man das in laufzeitabhängige Kalkulationszinsfüße umrechnen will, so könnte man äquivalente spot rates aus
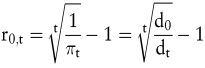
ableiten. Jedoch nutzen diese ebenso wenig wie Deans cut off rate, da man auch sie erst dann kennenlernt, wenn das Planungsproblem schon gelöst ist. Zwar kann man unter vereinfachenden Bedingungen Kanäle angeben, innerhalb derer sich die endogenen Kalkulationszinsfüße bewegen müssen, jedoch wird damit praktisch nicht allzu viel gewonnen.
Bisher ist die Problematik der Bestimmung von Kalkulationszinsfüßen nur unter Sicherheit angesprochen worden. In diesem Zusammenhang war es wichtig, die Mehrperiodigkeit von Investitionsentscheidungen stark zu betonen. Jetzt konzentrieren wir uns auf den Risikoaspekt und blenden den Zeitaspekt langfristiger Entscheidungen weitestgehend aus. Daher unterstellen wir im Folgenden, dass die zu bewertende Investition lediglich einen einmaligen Cashflow in der Zukunft verspricht. Dieser ist mit Hilfe des Kalkulationszinsfußes auf den Zeitpunkt t = 0 abzuzinsen, ist aber selbst leider nicht sicher. Als Diskontfaktor für risikobehaftete Cashflows, die der Investor im Zeitpunkt t=1 erwartet, können wir formal
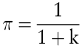
schreiben, wobei k für den Kalkulationszinsfuß bei Risiko steht.
1. Gewogene durchschnittliche Kapitalkosten
Wenn Entscheidungen mit Risiken verbunden sind, macht es Sinn, zwischen Eigen- und Fremdkapital zu unterscheiden. Gewöhnlich tragen Fremdkapitalgeber weniger Risiken als Eigentümer. Daher kann man davon ausgehen, dass Gläubiger geringere Renditen verlangen als Eigentümer. Bezeichnen wir den Fremdkapitalzinssatz mit kF und die von den Eignern verlangte Rendite mit kE, so liegt es nahe, für die gewogenen durchschnittlichen Kapitalkosten (weighted average cost of capital, WACC)
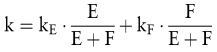
zu verwenden, wobei  für die Eigenkapitalquote für die Eigenkapitalquote
und 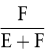 für die Fremdkapitalquote steht. Außerordentlich wichtig ist nun die Frage, ob kE und kF Größen sind, die (auch) von der Verschuldungspolitik des Investors abhängen. für die Fremdkapitalquote steht. Außerordentlich wichtig ist nun die Frage, ob kE und kF Größen sind, die (auch) von der Verschuldungspolitik des Investors abhängen.
Geht man von der Annahme aus, dass der Fremdkapitalkostensatz mit kF fixiert ist, und zwar unabhängig vom Ausmaß der Verschuldung, und unterstellt man ferner, dass die Eigentümer ihre Renditeforderung mit zunehmender Fremdfinanzierung anheben, und zwar entsprechend
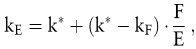
so belaufen sich die durchschnittlichen gewogenen Kapitalkosten stets auf
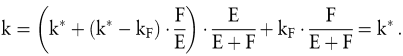
Dabei repräsentiert k* die Renditeforderung der Anteilseigner bei totaler Eigenfinanzierung, und das bemerkenswerte Ergebnis lautet, dass die durchschnittlichen Kapitalkosten vom Ausmaß der Verschuldung vollkommen unabhängig sind. Obwohl ein solches Resultat intuitiv nicht ohne weiteres einleuchten will, lässt es sich unter den Bedingungen eines perfekt funktionierenden Kapitalmarktes mit Hilfe von Arbitrageüberlegungen beweisen. Dieses Ergebnis verdanken wir Modigliani, /Miller, ).
2. Marktorientierte Kapitalkostenkonzepte
In beiden Ansätzen wird vorausgesetzt, dass k* größer als kF ist. Die Anteilseigner tragen (auch bei totaler Eigenfinanzierung) mehr Risiko als die Fremdkapitalgeber. Infolgedessen verlangen sie einen Kapitalkostensatz, der über dem Zinssatz für sichere Engagements liegt; sie verlangen eine Risikoprämie. Marktorientierte Kapitalkostenkonzepte unternehmen den Versuch, die Höhe einer angemessenen Risikoprämie zu objektivieren und nicht dem bloßen Fingerspitzengefühl zu überlassen.
Akzeptiert man die Grundidee, dass rationale Investoren nicht „ alles auf eine Karte setzen “ , sondern ihre Engagements so diversifizieren, dass die Gefahren aus einem Projekt durch die Chancen aus einem anderen Projekt wenigstens teilweise ausgeglichen werden, so kann man sich bei der Festlegung von Risikoprämien dem Capital Asset Pricing Model (CAPM) anvertrauen. Die Grundgleichung dieses Modells lautet
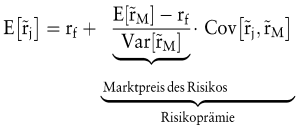
und besagt Folgendes: Die erwartete Rendite einer risikobehafteten Kapitalanlage E[rj] setzt sich additiv aus zwei Komponenten zusammen, und zwar dem Zinssatz für risikolose Kapitalanlagen rf und einer Risikoprämie. Diese wiederum besteht aus zwei Komponenten, und zwar dem Marktpreis des Risikos und der Menge des für die Kapitalanlage typischen Risikos. Letztere wird über die Kovarianz gemessen. Die Parameter in der Renditegleichung bedeuten im Einzelnen Folgendes:

Häufig präsentiert man dieselbe Renditegleichung auch in der Form

Hier steht βj für das sogenannte Beta der riskanten Investition. Der Index j, welcher in all diesen Gleichungen auftritt, ist nichts anderes als ein Zähler für die riskanten Investitionen, welche in der betrachteten Volkswirtschaft vorgenommen werden können, seien es nun Finanztitel (wie etwa Aktien oder Rentenpapiere), Sachinvestitionen oder Investitionen in Humankapital (Ausbildung).
Bevor wir nun auf die Ermittlung der Parameter, die in der CAPM-Gleichung auftreten, im Einzelnen eingehen, sei aber der Brückenschlag zum Kalkulationszinsfuß vorgenommen. Die Grundidee lautet: Die Kapitalkosten, welche ein Investitionsprojekt tragen muss, entsprechen der Rendite, die man am Kapitalmarkt für eine risiko-äquivalente Kapitalanlage erzielen könnte, also
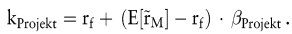
Will man dieses Konzept für die Beurteilung von Investitionsprojekten nutzen, so muss man die relevanten Parameter bestimmen.
Wegen der risikolosen Verzinsung rf empfiehlt es sich, auf die langfristige Umlaufrendite von Staatsanleihen zurückgreifen. Schwieriger wird es bei der erwarteten Marktrendite E[r?M]. Theoretisch ist das die Rendite, welche man erzielt, wenn man ein perfekt diversifiziertes Portfolio aus allen riskanten Kapitalanlagen erwirbt, die es in der Volkswirtschaft gibt. Als Näherungswert bietet sich die langfristige Rendite eines Aktienindex an.
Am schwierigsten ist die Abschätzung eines angemessenen Projekt-Betas. Dieses Beta informiert darüber, wie die Rendite des betrachteten Projektes mit der Rendite des Gesamtmarktes korreliert. Unterstellt man, dass es sich um eine Investition handelt, die von einer börsennotierten Publikumsaktiengesellschaft vorgenommen wird, so könnte man das Projekt-Beta (asset beta) aus dem Aktien-Beta (equity beta) ableiten. Für die im DAX vertretenen deutschen Aktiengesellschaften veröffentlicht das Handelsblatt täglich die equity betas auf der Grundlage der letzten 250 Börsentage. Wie bei Unternehmen vorgegangen werden kann, die nicht börsennotiert sind, wird in der Literatur eingehend erörtert.
Wie im Einzelnen vorzugehen ist, um aus beobachteten equity betas die gesuchten Projekt-Betas abzuleiten, lässt sich präzise nicht in der hier gebotenen Kürze beschreiben. Das liegt unter anderem daran, dass dabei auch steuerliche Einflüsse zu berücksichtigen sind, die an dieser Stelle mit den erforderlichen Details nicht dargestellt werden können. Zentral sind aber bei allen Techniken der Gewinnung angemessener Projekt-Betas folgende Überlegungen:
| 1. | Es ist ein equity beta zu bestimmen, bei dem das leistungswirtschaftliche Risiko dem Risiko des zu beurteilenden Projekts entspricht. Angenommen also, es geht um eine Investition im Geschäftsfeld A eines auf insgesamt fünf Geschäftsfeldern tätigen Unternehmens. Dann wäre es unangemessen, das equity beta des Gesamtunternehmens als Ausgangsgröße zu wählen, da sich in diesem Betafaktor auch die anderen vier Geschäftsfelder niederschlagen. | | 2. | Das equity beta ist unter Berücksichtigung des für das Unternehmen relevanten Steuersystems in Bezug auf die vom Investor gewünschte Zielkapitalstruktur zu adjustieren. In beobachtbaren historischen equity betas schlagen sich die historischen Kapitalstrukturen nieder, wobei gilt, dass die equity betas um so größer sind, je stärker ein Unternehmen verschuldet ist. Verfolgt nun der Investor eine Finanzierungspolitik, die darauf hinausläuft, die bisherige Kapitalstruktur zu ändern, so muss eine entsprechende Anpassung vorgenommen werden. Die Literatur stellt hierfür eine Reihe von (situationsabhängigen) Anpassungsformeln bereit. |
Bei der Frage, welchen Einfluss die Berücksichtigung von Steuern auf den Kalkulationszinsfuß hat, blenden wir die eben behandelten Risikoüberlegungen aus und gehen im Übrigen von flachen Zinsstrukturen aus.
1. Steuern bei vollkommenem Kapitalmarkt
Üblicherweise benutzt man das Standardmodell, wenn es darum geht, Kapitalwerte unter Einschluss von Steuern zu berechnen. Dieses Modell begegnet uns in zwei Varianten, je nachdem ob nur Ertragsteuern oder darüber hinaus auch Substanzsteuern berücksichtigt werden sollen.
Im einfachsten Fall konzentriert man sich auf eine allgemeine Gewinnsteuer mit proportionalem Tarif. Sie bemisst sich nach dem Periodenerfolg des Investors, welcher durch Zinserträge verstärkt und durch Zinsaufwendungen vermindert wird. Infolgedessen verwendet man in solchen Rechnungen einen versteuerten Kalkulationszinsfuß in Höhe von
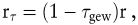
wobei τgew den Gewinnsteuersatz bezeichnet. Will man darüber hinaus Substanzsteuereinflüsse berücksichtigen, so muss man unterscheiden, ob die Substanzsteuer bei der Gewinnsteuer abzugsfähig ist oder nicht. Im ersten Fall verwendet man
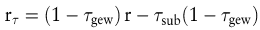
und im zweiten Fall

wobei τsub für den Substanzsteuersatz steht. Wie man die Gewinn- und Substanzsteuersätze mit Blick auf das in Deutschland geltende Steuersystem festlegt, ist in der einschlägigen Literatur (Mellwig, 1985; Wagner, F.W./Dirrigl, H. 1980) eingehend beschrieben worden.
2. Steuern bei unvollkommenem Kapitalmarkt
Verwendet man als Kalkulationszinsfuß die gewogenen durchschnittlichen Kapitalkosten, so muss von dem bisher beschriebenen Ansatz abgewichen werden. Der Grund besteht darin, dass Fremdkapitalzinsen in der Regel die Bemessungsgrundlage der Ertragsteuern mindern, Zinsen (Renditen) auf das Eigenkapital grundsätzlich aber nicht abgezogen werden dürfen, sondern als Gewinnbestandteile anzusehen sind. Beschränkt man sich auf die Berücksichtigung einer proportionalen Gewinnsteuer, so führt das auf einen Kalkulationszinsfuß in Höhe von
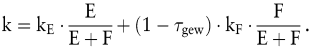
Die Einbeziehung von Substanzsteuern würde den bereits beschriebenen Leitlinien folgen.
Literatur:
Ballwieser, W. : Die Wahl des Kalkulationszinsfußes bei der Unternehmensbewertung unter Berücksichtigung von Risiko und Geldentwertung, in: BFuP 1981, S. 97 – 114
Brealey, R.A./Myers, S.C. : Principles of Corporate Finance, 6.A., New York 1999
Dean, J. : Capital Budgeting, 4. A., New York 1959
Fama, E.F. : Risk-Adjusted Discount Rates and Capital Budgeting under Uncertainty, In: Journal of Financial Economics 1977, S. 3 – 24
Hax, H. : Investitionstheorie, 4. A., Würzburg et al. 1985
Kruschwitz, L. : Investitionsrechnung, 8. A., München et al. 2000
Laux, H. : Kapitalkosten und Ertragsteuern, Köln et al. 1969
Mellwig, W. : Investition und Besteuerung, Wiesbaden 1985
Miles, J.A./Ezzel, J.R. : The Weighted Average Cost of Capital, Perfect Capital Markets, and Project Life: a Clarification, in: JFQA 1980, S. 719 – 730
Modigliani, F./Miller, M.H. : The Cost of Capital, Corporation Finance, and the Theory of Investment, in: AER 1958, S. 261 – 297
Moxter, A. : Die Bestimmung des Kalkulationszinsfußes bei Investitionsentscheidungen, in: ZfhF 1961, S. 186 – 200
Rudolph, B. : Kapitalkosten bei unsicheren Erwartungen, Berlin et al. 1979
Rudolph, B. : Klassische Kapitalkostenkonzepte zur Bestimmung des Kalkulationszinsfußes für die Investitionsrechnung, in: ZfbF 1986, S. 608 – 617
Rudolph, B. : Neuere Kapitalkostenkonzepte auf der Grundlage der Kapitalmarkttheorie, in: ZfbF 1986, S. 892 – 898
Schneider, D. : Investition, Finanzierung und Besteuerung, 7. A., Wiesbaden 1992
Siegel, T. : Der kontroverse Kalkulationszinsfuß. Diskussionspapier 17, hrsg. v. Inst. f. Wirtschaftswissenschaften der Techn. Univ. Berlin 1975
Wagner, F.W./Dirrigl, H. : Die Steuerplanung der Unternehmung, Stuttgart et al. 1980
Weber, M./Schiereck, D. : Marktbezogene Bestimmung der Kapitalkosten, in: Handbuch des Finanzmanagements, hrsg. v. Gebhardt, G./Gerke, W./Steiner, M.: München 1993, S. 131 – 150
|