II. Kostenverhalten bei axiomatischen Kostenfunktionen

1. Kostenfunktionen auf Basis der Produktionsfunktionstypen A – E

2. Kostenfunktionen bei alternativen Anpassungsarten der Potenzialfaktoren

a) Kostenverhalten bei kurzfristigen Anpassungsmaßnahmen

(1) Kostenverhalten bei quantitativ-zeitlicher Anpassung der Potenzialfaktoren

f1, Kf2, Kf3 (z.B. aufgrund von nutzungsabhängigen Abschreibungen und Instandhaltungsmaßnahmen, zusätzlichem Bedienungspersonal oder von Energieanlaufkosten), die zu Unstetigkeitsstellen in der Kostenfunktion führen. Zwischen den Unstetigkeitsstellen wird rein zeitliche Anpassung unterstellt, d.h. eine Maschine kann prinzipiell zwischen 0 Zeiteinheiten und der gesamten Zeitdauer einer Bezugsperiode laufen. Der Einsatzzeitraum von Arbeitskräften wird dagegen durch gesetzliche und tarifvertragliche Bestimmungen (z.B. Schichtzeit-, Pausen-, Ruhezeitregelungen) begrenzt.

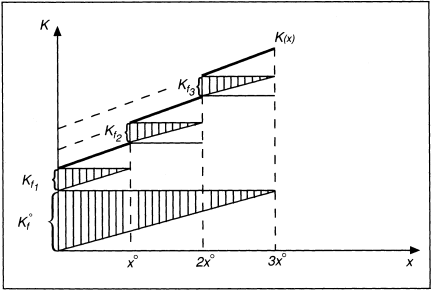
Abb. 1: Kostenverhalten bei quantitativ-zeitlicher Anpassung gleichartiger Potenzialfaktoren (Busse von Colbe, W./Laßmann, G. 1991)
Handelt es sich bei den Potenzialfaktoren um solche mit unterschiedlicher qualitativer Kapazität, so kann je Potenzialart ein unterschiedlich hoher Fixkostensprung und/oder Kostenanstieg bei quantitativ-zeitlicher Anpassung entstehen. Gutenberg (Gutenberg, E. 1983) spricht von selektiver Anpassung, wenn die Ingangsetzung/Stillsetzung der kostenunterschiedlichen Potenziale nach Gesichtspunkten der Kostenoptimierung vorgenommen wird.
Abb. 2 zeigt beispielhaft den optimalen Kostenverlauf für zwei Produktionsanlagen mit unterschiedlich hohen sprungfixen Kosten und unterschiedlich hohen Grenzkoten bei zeitlicher Anpassung. Für Produktmengen x < x(3) wird ausschließlich Anlage 1 aufgrund ihrer geringeren Fixkosten Kf1 genutzt. Dieser Vorteil ist bei der Produktmenge x(3) vollständig durch die geringeren variablen Kosten der Anlage 2 kompensiert (Schnittpunkt von K1(x) wird K2(x)). Für Produktmengen x(3) < x ≤ x(2) wird ausschließlich Anlage 2 eingesetzt. Bei Produktmengen x > x(2) wird die über x(2) hinausgehende Menge auf der zusätzlich zu Anlage 2 eingesetzten Anlage 1 produziert, sodass für die optimale Anpassung die Kostenfunktion EABCD gilt. Fallen die fixen Kosten Kf1 und Kf2unabhängig davon an, ob die Anlagen in Betrieb sind oder nicht, so gilt die Kostenkurve FCD: Für alle Produktmengen x ≤ x(2) wird die Anlage 2 aufgrund ihrer niedrigeren variablen Stückkosten allein verwendet; auf Anlage 1 werden nur Produktmengen x > x(2) hergestellt.

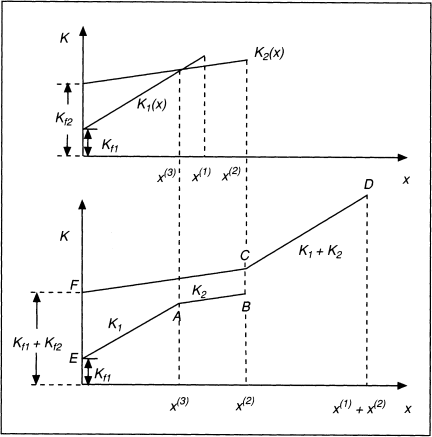
Abb. 2: Kostenfunktionen bei quantitativ-zeitlicher Anpassung qualitativ unterschiedlicher Potenzialfaktoren (Busse von Colbe, W./Laßmann, G. 1991)

(2) Kostenverhalten bei intensitätsmäßiger Anpassung

Bei Potenzialfaktoren führt die Veränderung der Mengenleistung je Zeiteinheit zu einer nicht linearen Variation des Bedarfs einiger Verbrauchsfaktoren wie z.B. Energie. Sind für das Betreiben eines Aggregats j mehrere Verbrauchsfaktoren vi erforderlich und liegt – bei Verbrauchsfaktorbewertung mit konstanten Beschaffungspreisen qi0  – der kostengünstigste Durchschnittsverbrauch v¯ij jeweils bei unterschiedlichen Intensitäten di(1) und dj(2), so ist gem. Abb. 3 zunächst durch Addition der faktorbezogenen Durchschnittskostenfunktionen k1j, k2j und k3j eine aggregatbezogene Durchschnittskostenfunktion kj zu bilden.

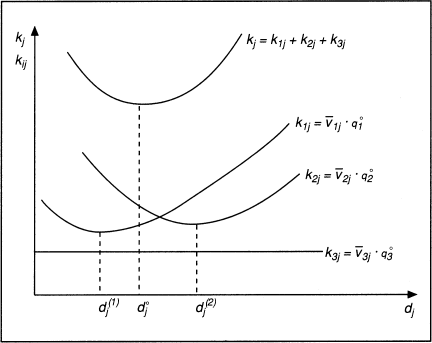
Abb. 3: Ermittlung der kostenoptimalen Intensität bei drei Einsatzfaktoren (Busse von Colbe, W./Laßmann, G. 1991)
Im Minimum dieser Durchschnittskostenfunktion liegt die kostenoptimale Intensität dj0 des Aggregats. Wird bei intensitätsmäßiger Anpassung unter speziellen Voraussetzungen Intensitätssplitting angenommen, so folgt daraus wiederum eine Kostenfunktion mit Unstetigkeitsstellen.
Aus den aggregatbezogenen Funktionen kj lassen sich bei konstanter zeitlicher Nutzung tj0 die in Abb. 4 dargestellten Gesamtkostenfunktionen Kj(dj,tj0) ableiten, die – bei anderen Ausgangsbedingungen  – den Verlauf der ertragsgesetzlich bestimmten Kostenfunktion entsprechen. Die Kombination von zeitlicher und intensitätsmäßiger Anpassung bei variierenden Produktmengen je Bezugsperiode führt zu einer dreidimensionalen Kostenfunktion gemäß Abb. 4.

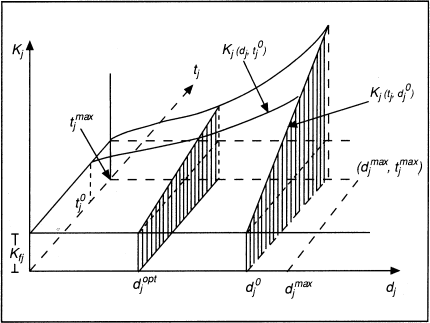
Abb. 4: Kostenverhalten bei quantitativ-zeitlicher und intensitätsmäßiger Anpassung der Potenzialfaktoren (Busse von Colbe, W./Laßmann, G. 1991)

b) Kostenverhalten bei langfristigen Anpassungsmaßnahmen (totaler Anpassung)

Langfristig können alle Produktionsfaktoren an alternative Ausbringungsmengen angepasst werden. Es ergeben sich vielfältige Investitions- bzw. Desinvestitionsprobleme. Die Produktionstheorie geht dabei in die Investitionstheorie über. Der Verlauf der langfristigen Kostenfunktion wird ähnlich wie der einer kurzfristigen Kostenfunktion von der Art der Anpassung der Faktoreinsatzmengen an unterschiedliche Produktmengen bestimmt (Busse von Colbe, W./Laßmann, G. 1991). Hierbei sind zwei Fälle zu unterscheiden (Gutenberg, E. 1983):
(1) Multiple Anpassung: Mit der Betriebsgrößenvariation ist keine Umgestaltung der eingesetzten Produktionsverfahren verbunden, d.h. alle Faktoreinsatzmengen werden im gleichen Verhältnis vermehrt oder vermindert. Unter der vergröbernden Annahme vollständiger Teilbarkeit bzw. Abbaubarkeit der Potenzialfaktoren lässt sich eine durch den Koordinaten-Nullpunkt verlaufende, linear ansteigende Gesamtkostenfunktion mit konstanten Grenz- und Durchschnitts-Stück-Kosten ableiten. Multiple Faktorvermehrungen sind allerdings nur bis zu einer bestimmten Unternehmensgröße und bezogen auf einzelne Teilbetriebe eines Unternehmens plausibel. In der Realität lassen sich auch Potenzialfaktoren mit konstanten Einsatzmengen beobachten (z.B. Unternehmensführung mit ihren Zentralverwaltungsstellen).
(2) Mutative Anpassung: Die Betriebsgrößenvariation ist mit einer produktionstechnischen Verfahrensneu- oder -umgestaltung verbunden (Anwendung rationellerer Technologien, größere Aggregate u. dgl.). Mit steigenden Faktoreinsatzmengen wird die Qualität der Faktoren geändert. Z.B. steigen bei einigen Fertigungsanlagen nach der so genannten »0,6 rule« innerhalb gewisser Kapazitätsbereiche die Investitionsausgaben in der Potenz 0,6 – 0,7 der Kapazitätszunahme (Busse von Colbe, W./Laßmann, G. 1991, S. 294). Daraus folgt ein entsprechend verringerter Anstieg der Abschreibungs- und Zinskosten. Durch Veränderung der Faktorqualitäten, Faktorproportionen und Faktorgrößen lassen sich Kosteneinsparungen je Produkteinheit erzielen. Die Steigerung der langfristigen Gesamtkostenkurve verläuft dann zumindest in gewissen Grenzen degressiv.

3. Kostenverhalten bei alternativen Produktionsprozessbedingungen

In der bwl. Modelltheorie werden für verschiedene Aufgabenstellungen zur Gestaltung der Prozessbedingungen Kostenfunktionen zur Veranschaulichung optimaler Handlungsanleitungen herangezogen. Ausgangspunkt sind Überlegungen zu handlungsbedingt gegenläufigem Kostenverhalten. Beispiele bilden die Bestimmung kostenoptimaler Bestell- und Fertigungslosgrößen sowie Instandhaltungs- und Qualitätssicherungsstrategien (vgl. Abb. 5).

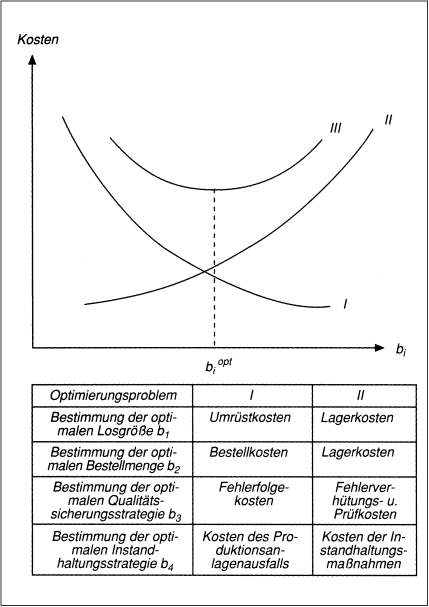
Abb. 5: Bestimmung kostenoptimaler Einflussgrößewerten biopt
Aus dem Kostenminimum der Summenkostenfunktion III zweier entgegengesetzt verlaufender Kostenfunktionen I und II lässt sich eine kostenoptimale Fixierung der Kosten-Einflussgröße bi (z.B. kostenoptimale Losgröße, Bestellmenge, Qualitätssicherungsintensität, Instandhaltungsintensität) ableiten. In der Praxis des Rechnungswesens können die Funktionen I und II nicht mit den erforderlichen Kosteninformationen unterlegt werden, da die Einflussgrößenbeziehungen sehr komplex und zum großen Teil nicht quantifizierbar sind. Trotzdem besitzt der ökonomische Denkansatz durchaus Handlungsrelevanz. So wird man z.B. bei hohen Reklamationskosten zusätzlich Qualitätssicherungsmaßnahmen (z.B. zusätzliche Prüfvorgänge) durchführen, solange die dadurch entstehenden Kosten die eingesparten Reklamationskosten nicht überschreiten (Hahn, D./Laßmann, G. 1999). Es gibt in der Praxis viele Heuristiken zur Auffindung nahoptimaler Werte für bi, sodass man nicht nur auf Versuchs-Irrtums-Iterationen angewiesen ist.

III. Kostenverhalten bei empirischen Kostenfunktionen

1. Bedeutung von Engineering Production Functions und Betriebsmodellen für das Kostenverhalten

Im Gegensatz zu den formal allgemein gültigen Aussagen über das Kostenverhalten bei axiomatisch begründeten deterministischen Produktionsbedingungen basieren die im Folgenden zu behandelnden Kostenfunktionen auf empirisch abgesicherten Produktionsverhältnissen konkreter Betriebs- und Arbeitssysteme. Auf ingenieurwissenschaftlicher Basis wurden von Chenery (Chenery, H. B. 1949) und Ferguson (Ferguson, A. R. 1950) Verbrauchsfunktionen und darauf aufbauende Kostenfunktionen für bestimmte Typen von Flugzeugmotoren entwickelt. In Deutschland hat vor allem Pichler (Pichler, O. 1961) für Raffineriebetriebe statistisch abgesicherte Input-/Outputmodelle aufgestellt, durch deren Bewertung Kosten und Erlöse für geplante Produktions- und Absatzprogramme unter bestimmten Betriebs- und Marktbedingungen abgeleitet werden, die nur für eine konkrete historische Situation Gültigkeit besitzen. Das von Pichler entwickelte Konzept hat R. Wartmann fortgeführt und durch umfangreiche Regressionsanalysen sowie Auswertung naturwissenschaftlicher Gesetzmäßigkeiten ein Hochofenmodell aufgestellt. Die Verbräuche an Erz, Koks, Zusatzstoffen, Sauerstoff, elektrischer und anderer Energie hängen in Hochofenwerken nicht nur von der Menge und Qualität des herzustellenden Roheisens, sondern von einer Vielzahl verfahrenstechnischer Bedingungen ab. Die komplexen, z.T. nicht linearen Beziehungszusammenhänge zwischen Produktprogramm, Kosteneinflussgrößen und Verbrauchsgütermengen lassen sich in multivariablen Einflussgrößenfunktionen erfassen und für Zwecke der Prozesssteuerung in ein mehrstufiges Input-/Outputrechenmodell einbringen. Für bwl. Anwendungen der Planung, Budgetierung und Kostenermittlung reichen i.d.R. linearisierte Näherungsfunktionen aus. Die Anwendung von Input-/Outputrechenmodellen ist insb. bei komplexen Produktionsverhältnissen mit verfahrensbedingten Freiheitsgraden sinnvoll, z.B. bei variablen Rohstoffmischungen, Losgrößen und -reihenfolgen oder technischen Verfahrensalternativen, wie sie auch in Aluminium- und Kupferhütten sowie chemischen Grundstoffgewinnungsbetrieben vorherrschen.
Multivariable lineare Funktionssysteme ermöglichen die Verwendung der Matrizenrechnung für Simulationsrechnungen und einfache Ermittlungsrechnungen sowie z.T. auch für Optimierungsrechnungen. Hierfür haben Wartmann/Steinecke/Sehner eine umfassende Konzeption (Integrative Strukturmatrix) aufgestellt, die für Zwecke der Produktions- und Faktorbedarfsplanung sowie Kostenplanung generell zur Anwendung gebracht werden kann. Unter Anleitung von G. Laßmann sind für mehrere konkrete Betriebe mithilfe von multivariablen Regressionsanalysen Betriebsmodelle für bwl. Planungs- und Überwachungsaufgaben aufgestellt worden. Eine Energieverbrauchsfunktion hängt z.B. von verschiedenen Einsatzzeitarten und -zeitpunkten einzelner Arbeitssysteme – bezeichnet als sekundäre Einflussgrößen – ab. Diese werden wiederum von Vorgaben über das Produktprogramm und die betriebliche Verfahrensweise – bezeichnet als primäre Einflussgrößen – bestimmt. Aus den primär vorzugebenden Einflussgrößen lassen sich zunächst die verbrauchsspezifischen sekundären Einflussgrößenwerte für einen Betrieb ableiten, und daraus resultieren dann die gesuchten Planverbrauchsmengen z.B. an Energie. Durch Bewertung der Verbrauchsmengen erhält man in Vorausrechnungen geplante Kosten, in Nachrechnungen Istkosten; darauf aufbauend können die üblichen Abweichungsanalysen nach dem Konzept der Plankostenrechnung vorgenommen werden. Das System ist in der Literatur unter der Bezeichnung »Betriebsplanerfolgsrechnung« beschrieben und umfasst in Analogie zur Kostenseite auch die Erlöse (Hahn, D./Laßmann, G. 1999).

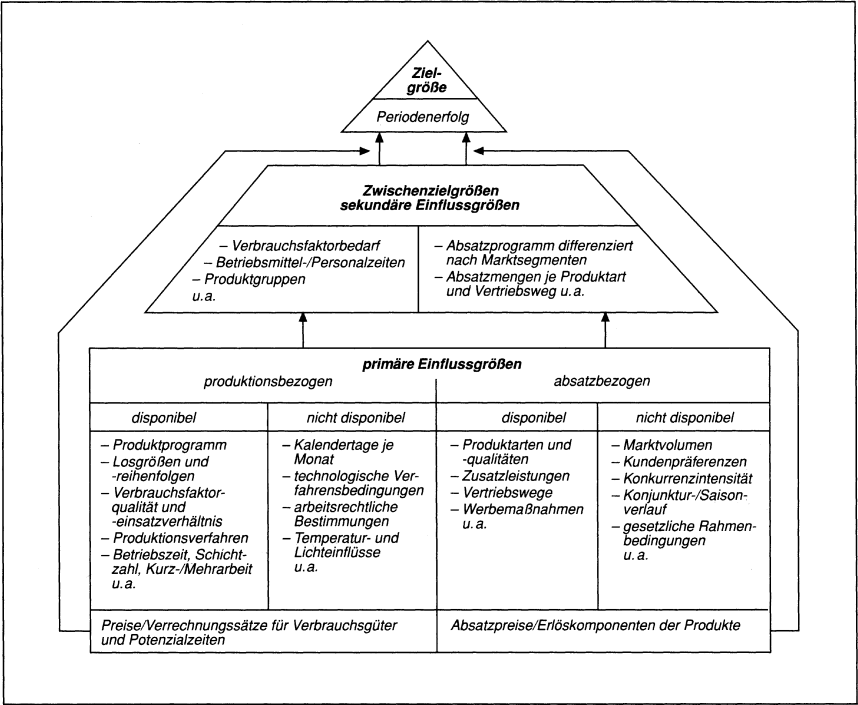
Abb. 6: Ursachen-Wirkungszusammenhänge in der Betriebsplanerfolgsrechnung (Hahn, D./Laßmann, G. 1999)

2. Bedeutung von Erfahrungskurven und Kostenremanenzen für das Kostenverhalten

Vor allem in der Literatur zur strategischen Unternehmensplanung wird vielfach für innovative Produkte ein Konzept der Kostenerfahrungskurve zugrunde gelegt (Henderson, B. D. 1984). Dabei werden auf der Abszisse die Zeit bzw. die kumulierte Produktmenge und auf der Ordinate die Stückkosten abgetragen. Jede Verdoppelung der Produktmenge führt zu einem Kostensenkungspotenzial von mindestens 20% der Wertschöpfungskosten pro Stück bis maximal 30% der vollen Stückkosten (Gälweiler, A. 1992), sodass die Stückkostenfunktion einen L-förmigen Verlauf aufweist. Zurückgeführt wird dies auf Lerneffekte aus der Spezialisierung, ansteigende Losgrößen, Innovationen und Größendegressionen (z.B. bei Elektronikprodukten). Nach Erkenntnissen der Lerntheorie sinkt mit jeder Verdoppelung der im Produktionsbereich durchzuführenden Verrichtungen durch Arbeitskräfte der dafür benötigte Zeitbedarf auf z.B. 85% des jeweils vorhergehenden Zeitbedarfs. So werden von der Automobilindustrie in langfristigen Verträgen über Neuteile mit den Zulieferern sog. Savings vereinbart, nach denen die Lieferpreise jährlich um mehrere Prozentpunkte im Hinblick auf zu erwartende Kostensenkungen reduziert werden müssen. Einer Kosten- bzw. Preisdegression können allerdings inflationäre Wirtschaftsentwicklungen und/oder Produktqualitätsverbesserungen entgegenwirken (z.B. bei Pkw in den letzten Jahrzehnten).
Ein tendenziell gegenteiliges Kostenverhalten stellt das empirisch belegte Phänomen der Kostenremanenz dar. Während in der deterministischen Produktions- und Kostentheorie jeder Produktmenge ein Kostenbetrag eindeutig zugeordnet und damit die Frage eines unterschiedlichen Kostenverhaltens bei zunehmender gegenüber abnehmender Beschäftigung vernachlässigt wird, zeigt sich in der Realität, dass bei rückläufiger Beschäftigung vielfach ein höheres Kostenniveau entsteht, als es im Zuge aufsteigender Beschäftigung bei gleicher Produkt- und Absatzmenge gegeben war. Dies hängt insb. damit zusammen, dass Arbeitnehmerzahlen und Personalvergütungen bei rückläufiger Beschäftigung, z.B. durch entstehende Sozialplankosten und Verdienstsicherungsklauseln in Tarifverträgen, nicht bedarfsgerecht angepasst werden können. Auch können vielfach die Kosten für Infrastruktureinrichtungen (Transporteinrichtungen, Beleuchtungs-, Heizenergie-, Raumkosten u. dgl.) nicht an die verminderte Kapazitätsnutzung der Arbeitssysteme entsprechend den Werten bei wachsender Beschäftigung angeglichen werden (Schmalenbach, E. 1963).

IV. Einsatz von Kostenfunktionen als Controllinginstrumente

Für die Kostenplanung und -überwachung werden heute überwiegend monofunktionale lineare Abhängigkeiten zwischen Kosten und Beschäftigung nach dem Muster K = Kf + x · kv zugrunde gelegt. Auch das System der Grenzplankosten- und Deckungsbeitragsrechnung nach Kilger (Kilger, W. 1993) beruht grundsätzlich auf beschäftigungsunabhängigen (fixen) und linear beschäftigungsabhängigen (variablen) Kostenanteilen je Kostenart. Dabei kann je nach Länge des Betrachtungszeitraums sowie nach realisierten Produktionsverfahren oder -bedingungen eine unterschiedliche Aufteilung nach Fix- und Proportionalanteilen je Kostenart in den verschiedenen Kostenstellen vorgenommen werden. In der Praxis begnügt man sich jedoch i.d.R. mit sehr pauschalen Aufteilungen in produktproportionale Kostenanteile und Fixkosten der Betriebsbereitschaft (einfach flexible Plankostenrechnung). Die darauf aufbauenden Kostenbudgetierungen und Kostenvorgaben für Soll-/Istvergleiche müssen bei den überwiegend vorherrschenden Betriebsbedingungen zu ungenauen Ergebnissen führen. Dies ist aus theoretischer Sicht unbefriedigend und genügt auch nicht den Anforderungen eines leistungsfähigen Produktionscontrolling.
Nur eine differenzierte Erfassung aller wesentlichen Kosten- und Erlöseinflussgrößen (mehrfach flexible Plankostenrechnung/Betriebsplanerfolgsrechnung) kann zu hinreichend abgesicherten Planungswerten und Vorgabegrößen für die Betriebsüberwachung führen (Hahn, D./Laßmann, G. 1999). Die in Tab. 1 enthaltene Übersicht über kurz- und langfristig disponierbare Größen, die für den Faktorverbrauch und damit für die spezifische Kostenentstehung maßgebend sind, dokumentiert, welchen Differenzierungsgrad ein Kostenplanungssystem erfüllen muss, damit für unterschiedliche Produktprogramme, Produktionsbedingungen und -verfahren sowie Materialmischungsverhältnisse und Beschaffungspreise das jeweilige Kostenverhalten hinreichend genau vorausberechnet und für Planungs-, Steuerungs- und Überwachungsaktivitäten zugrunde gelegt werden kann. Darauf hat bereits Henzel in den 1930er-Jahren hingewiesen (s. Henzel, F. 1962).

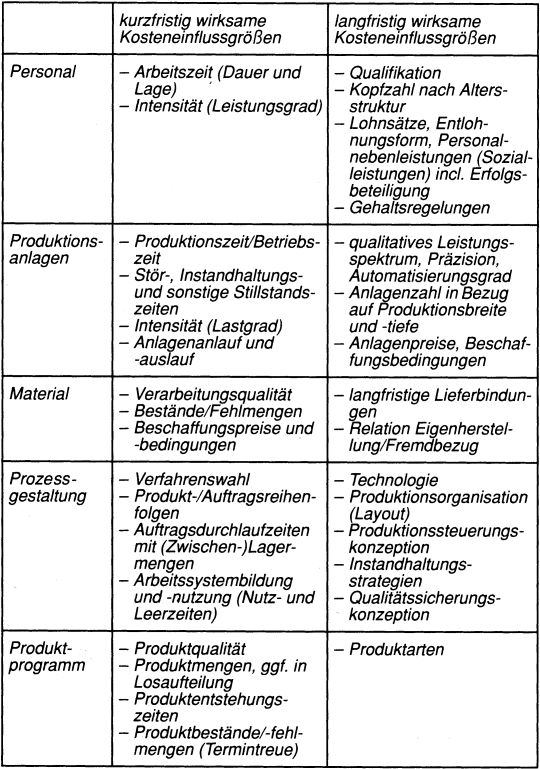
Tab. 1: Kurz- und langfristig disponible Kosteneinflussgrößen (ähnlich Hahn, D./Laßmann, G. 1999)
Literatur:
Busse von Colbe, W./Laßmann, G. : Betriebswirtschaftstheorie, Bd. 1: Produktions- und Kostentheorie, 5. A., Berlin et al. 1991
Chenery, H. B. : Engineering Production Functions, in: QJE, 1949, S. 507 – 531
Ferguson, A. R. : Empirical Determination of Multidimensional Marginal Cost Function, in: Ec, 1950, S. 217 – 235
Franke, R. : Betriebsmodelle, Düsseldorf 1972
Gälweiler, A. : Determinanten des Zeithorizonts in der Unternehmensplanung, in: Strategische Unternehmensplanung, hrsg. v. Hahn, D./Taylor, B., Heidelberg et al. 1992, S. 203 – 220
Gutenberg, E. : Grundlagen der Betriebswirtschaftslehre, Bd. 1: Die Produktion, 24. A., Berlin et al. 1983
Hahn, D./Laßmann, G. : Produktionswirtschaft – Controlling industrieller Produktion, Bd. 3, 1. u. 2. Teilbd., Heidelberg 1993
Hahn, D./Laßmann, G. : Produktionswirtschaft – Controlling industrieller Produktion, Bd. 1 und 2, 3. A., Heidelberg 1999
Heinen, E. : Betriebswirtschaftliche Kostenlehre, 6. A., Wiesbaden 1983
Henderson, B. D. : Die Erfahrungskurve in der Unternehmensstrategie, 2. A., Frankfurt 1984
Henzel, F. : Neuere Tendenzen auf dem Gebiete der Kostenrechnung, in: ZfhF, 1962, S. 347 – 370
Kilger, W. : Flexible Plankostenrechnung und Deckungsbeitragsrechnung, 10. A., Wiesbaden 1993
Kloock, J. : Betriebswirtschaftliche Input-Output-Modelle, Wiesbaden 1969
Küpper, H.-U. : Dynamische Produktionsfunktion der Unternehmung auf Basis des Input-Output-Ansatzes, in: ZfB, 1979, S. 93 – 106
Laßmann, G. : Betriebsplankostenrechnung, in: HWR, hrsg. v. Chmielewicz, K./Schweitzer, M., 3. A., Stuttgart 1993, Sp. 168 – 183
Marshall, A. : Principles of Economics, 8. A., London 1961
Pichler, O. : Kostenrechnung und Matrizenkalkül, in: APF, 1961, S. 29 – 46
Schmalenbach, E. : Kostenrechnung und Preispolitik, 8. A., Köln et al. 1963
Walter, K. D. : Gestaltung und Verwirklichung linearer Modelle zur Unternehmensplanung, Bochum 1977
Wartmann, R./Steinecke, U./Sehner, G. : System der Plankosten- und Planungsrechnung mit Matrizen, IBM-Form: GE 12 – 1345 – 0, Düsseldorf 1975
Wittenbrink, H. : Kurzfristige Erfolgsplanung und Erfolgskontrolle mit Betriebsmodellen, Wiesbaden 1975