|
Break-even-Analyse
Inhaltsübersicht
I. Kurzcharakteristik und Ursprünge
II. Grundmodell der Break-even-Analyse
III. Weitere Varianten der Break-even-Analyse
IV. Erweiterungen der Break-even-Analyse
V. Zusammenfassende Würdigung
I. Kurzcharakteristik und Ursprünge
Break-Even-Analyse (BEA) ist die Bezeichnung für Auswertungsrechnungen zur Ermittlung des Break-even-Punktes (BEP). Hierin entsprechen sich zwei Funktionen, die von derselben Variablen abhängig sind. In dem Grundmodell kann es sich um linear von der Absatzmenge oder dem Absatzwert abhängige Funktionen, wie die Umsatz- (total income from sales) und die Kostenfunktion (total cost of sales), handeln (vgl. unter II.1.). Dieses Konzept findet auch Anwendung in der Definition des Cournot\'schen Punktes, im Rahmen der Ermittlung interner Zinsfüße von Investitionsobjekten (Kilger, W. 1965) oder in Kapital-Budgetierungs-Modellen (Dean, J. 1969). BEA werden weiterhin unter die Instrumente der Führungsunterstützung (Haidacher, O.B. 1969), der Erlösplanung und Erlöskontrolle (Dammann, W. 1963) und unter die – auf die Ermittlung kritischer Werte zielenden – Sensitivitätsanalysen eingeordnet.
BEA sind seit langem gebräuchlich, weit verbreitet (Schweitzer, M./Troßmann, E. 1998, S. 15 ff. und 353 ff.) und auch unter Bezeichnungen, wie Deckungspunkt-, Gewinn- oder Nutzschwellen-Analyse, Kosten-Nutzen-Analyse bzw. Cost-Volume-Profit-Analysis (CVPA) anzutreffen. Als „ Begründer “ der BEA gelten im deutschsprachigen Schrifttum Bücher (Bücher, K. 1910) und Schär (Schär, J.F. 1911) und im englischsprachigen Schrifttum Mann (Mann, J. 1904), Williams (Williams, J.H. 1922), Rautenstrauch (Rautenstrauch, W. 1930) und Knoeppel (Knoeppel, C.E. 1933) bzw. Knoeppel/Seybold (Knoeppel, C.E./Seybold, E.G 1937). Der Ausgangspunkt dürfte nach Haidacher (Haidacher, O.B. 1969, S. 172 ff.) jedoch früher liegen (Babbage, C. 1833; Lardner, D. 1850; Hess, H. 1903/1904).
Das ursprüngliche Konzept einer BEA dient einer Erfolgsanalyse auf der Grundlage von Kosten und Erlösen, indem jener Punkt bestimmt wird, bei dem die vollen Kosten die Umsatzerlöse gerade decken. Bei dieser kritischen Beschäftigung (und Ausbringungsmenge) beträgt der Gewinn Null. Er muss erreicht werden, „ um das eingesetzte Kapital in seiner ursprünglichen Höhe zu erhalten “ (Haidacher, O.B. 1969, S. 15). Synonym wird der BEP unter anderem als „ Deckungsauflage, Deckungspunkt, Erfolgsschwelle, Gewinnschwelle, kritischer Punkt, Nutz(en)schwelle, Rentabilitätsschwelle, toter Punkt, Vollkostendeckungspunkt “ (Schweitzer, M./Troßmann, E. 1998, S. 15) bezeichnet.
II. Grundmodell der Break-even-Analyse
1. Prämissen und Lösungskonzepte
Den BEP, also die kritische Beschäftigung, deren Überschreiten zum Eintritt in die Gewinnzone führt, ermittelt man im Grundmodell der BEA aus der BEA-Grundgleichung (Gleichung 1) unter restriktiven Prämissen (Coenenberg, A.G. 1999, S. 301 f.; Schweitzer, M./Troßmann, E. 1998, S. 53 f.):
| - | Gewinnstreben ist ein vordringliches Unternehmensziel. | | - | In einem Ein-Produkt-Unternehmen wird einstufig produziert (keine (mehrstufige) Variantenfertigung). | | - | Die Menge des betrachteten Produkts ist die einzige Aktionsvariable (einziger Kostentreiber, Umsatztreiber, Gewinntreiber). | | - | Alle Daten und Beziehungen, wie Kapazitäten, Absatzorganisation, Produktionsverfahren, Stückerlöse und variable Stückkosten sowie fixe Kosten, sind für den Untersuchungszeitraum bekannt, sicher und konstant. |
Unterstellt wird somit die Zurechenbarkeit aller Fixkosten zu dem Erzeugnis und eine Invarianz von Fixkosten und variablen Stückkosten in Bezug auf Produktionsverfahren (keine Verfahrenswechsel) sowie Produktionsmenge (keine intervallfixen Kosten bzw. Kostenremanenzen, Losgrößenvorteile, Preissteigerungen bei den Inputfaktoren, Kostendegression (Erfahrungskurve usw.). Analog bildet die Umsatzfunktion weder zeitliche, regionale, mengen- oder abnehmerbezogene Preisdifferenzierungen noch fixe Erlöse ab (zum Beispiel bei der Bahncard). Schließlich darf keine Lagerhaltung vorliegen (Identität von Produktions- und Absatzmenge).
Die Ausgestaltungsformen einer BEA ergeben sich aus grundlegenden Umformungen der Gewinnfunktion (zum Beispiel als Umsatz-Gesamtkosten-Modell oder als (Fixkosten-) Deckungsbeitrags-Modell).

Linear von der Produktions- bzw. Absatzmenge (x) abhängig sind die Funktionen Periodenerfolg (G), Umsatzerlöse (U) und Gesamtkosten (K), nicht aber Stückerlös (p), volle Stückkosten (k), variable Stückkosten (kv) und Fixkosten (Kf).
Abb. 1 zeigt das Umsatz-Gesamtkosten-Modell (durchgezogene Linien) und das Deckungsbeitrags-Modell (gestrichelte Linien) in einer Graphik. Sie verdeutlicht, dass ein Wechsel der Zonenzugehörigkeit (Verlustzone oder Gewinnzone) durch Erhöhung der absetzbaren Beschäftigung an die Existenz fixer Kosten gebunden ist. Erfolgsoptimal ist die maximal realisierbare Ausbringungsmenge.
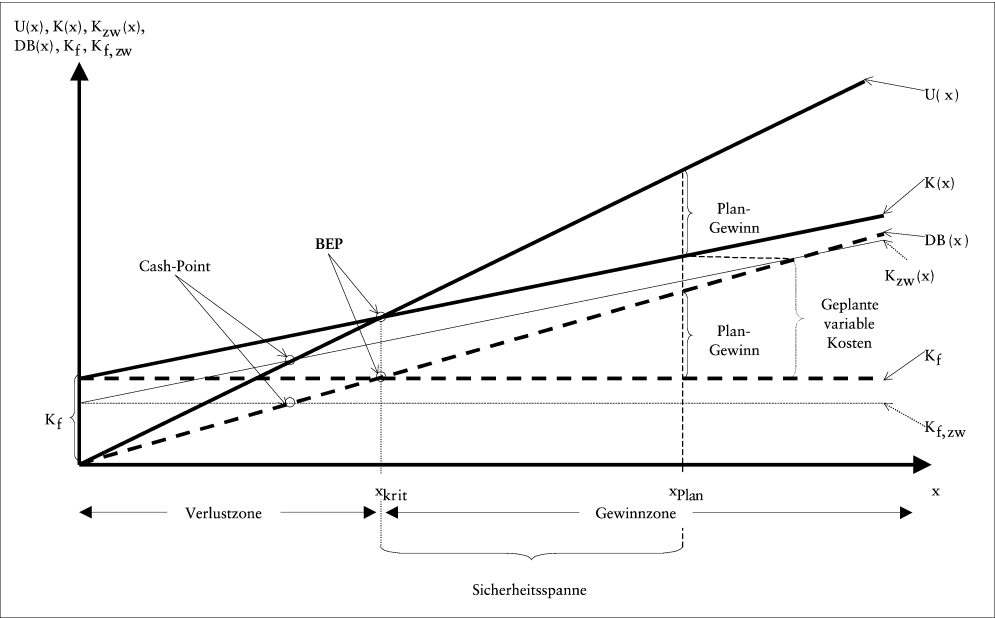
Abb. 1: Break-even-Analyse im Umsatz-Gesamtkosten-Modell und im Deckungsbeitrags-Modell
Die kritische Beschäftigungs- bzw. (Mindest-)Absatzmenge (BEP bzw. xkrit) ergibt sich rechnerisch als Quotient aus Periodenfixkosten und Deckungsbeitrag:
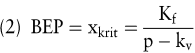
Alternativ kann auf den wertmäßigen Absatz abgestellt werden. Durch Umformungen von Gleichung (2) ergibt sich der (kritische) Break-even-Umsatz (BEU bzw. Ukrit) als Quotient aus Fixkosten und der – zur erfolgsabhängigen Bemessung von Provisionen dem Umsatz überlegenen – Deckungsquote (auch Deckungsbeitrags-Umsatz-Faktor; DBU-Faktor):
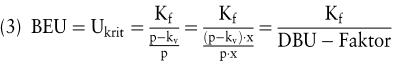
Insofern sind erstens BEA-Grundmodell und Direct Costing/Deckungsbeitragsrechnung konzeptionell verwandt und zweitens die Spaltung der Gesamtkosten in variable und fixe Kosten eine unverzichtbare Anwendungsvoraussetzung einer BEA (Dean, J. 1952).
2. Grundlegende Auswertungsmöglichkeiten von Umsatz-Gesamtkosten- und Deckungsbeitrags-Modell (Grundmodell)
Umsatz-Gesamtkosten-Modell und Deckungsbeitrags-Modell weisen gemäß Abb. 1 übereinstimmend einen in der Gewinnzone liegenden BEP für die geplante (prognostizierte) Beschäftigungsmenge (xPlan) aus. Um einen höheren Gewinn zu erzielen, gibt es zwei kombinierbare Ansatzpunkte: Mengensteigerung oder Vorverlagerung des BEP bei unveränderter Produktions- bzw. Absatzmenge. Letzteres kann durch Verschiebungen oder Drehungen der in Abb. 1 gezeigten Funktionen als Folge höherer Absatzpreise bzw. niedrigerer fixer oder variabler Kosten erreicht werden. Variiert man zum Zwecke preispolitischer Analysen in einem Deckungsbeitrags-Modell Stück-Deckungsbeiträge in kleineren Abständen, ergibt sich eine Schar von Deckungsbeitragsgeraden (sog. Deckungsbeitragsspinne; Kleinebeckel, H. 1976, S. 58). In Abb. 1 wird auch ein sog. Cash-Point ausgewiesen. Es handelt sich um den Schnittpunkt von Deckungsbeitragsstrahl (Umsatzstrahl) und der Funktion der zahlungswirksamen fixen Kosten Kf,zw (zahlungswirksamen Gesamtkosten Kzw(x)).
Die differenzierte Überprüfung der Zugehörigkeit des Datenkranzes der Planung zur Gewinn- oder Verlustzone erfolgt insbesondere durch Bildung von Relativziffern (Salden). Dabei werden Plan-Produktionsmenge, -Kapazitätsauslastung, -Absatzmenge, -Umsatz usw. im Zähler (Minuend) und die jeweiligen Break-even-Werte im Nenner (oder Subtrahend) berücksichtigt. Sind die Werte der Quotienten (Salden) kleiner als eins (kleiner als Null), wird die Gewinnzone verfehlt.
Die im Umsatz-Gesamtkosten-Modell und im Deckungsbeitrags-Modell übereinstimmende und als absoluter Abstand von BEP/BEU zu einer geplanten Beschäftigung zu berechnende Sicherheitsspanne soll zum Beispiel eine Beurteilung darüber erlauben, wie „ sicher “ eine prognostizierte Gewinnerzielung ist. Wird die Sicherheitsspanne in Prozent der Plan-Beschäftigung ausgedrückt, spricht man von einem Sicherheitskoeffizienten (S):
Einzelkaufleute und Personen

Positive (negative) Werte für S bringen zum Ausdruck, um wie viel Prozent die in Geldeinheiten geplante Absatz- bzw. Produktionsmenge bis zum Erreichen des BEP sinken kann (steigen muss). Analog ist der Operating Leverage (OL) zu interpretieren. Diese Bezeichnung trägt die Kennzahl relative Gewinnänderung zu relativer Umsatzänderung. Letztlich handelt es sich hierbei um den Kehrwert von S. Jedoch sind S und OL „ ohne explizite Berücksichtigung von Wahrscheinlichkeitsverteilungen mit gewisser Vorsicht zu genießen “ (Ewert, R./Wagenhofer, A. 2000, S. 226).
Beide in Abb. 1 gezeigten Modelle zeichnen sich durch große Anschaulichkeit aus (vgl. Abb. 1). Aber das Deckungsbeitrags-Modell ist einprägsamer und leichter lesbar. Andererseits weisen beide Modelle explizit unterschiedliche Informationen zu den Determinanten des BEP aus. So ist aus dem Umsatz-Gesamtkosten-Modell (Deckungsbeitrags-Modell) die Höhe der (Stück-)Deckungsbeiträge [variablen (Stück-)Kosten] nicht ersichtlich.
Die Anschaulichkeit einer BEA wird durch einen restriktiven Prämissenkatalog erkauft (vgl. unter II.1.). Daher kann ein Break-even-Chart nur in einem engen Intervall um die geplante (ganzzahlige!) Produktions- und Absatzmenge bzw. Kapazitätsauslastung intensiv ausgewertet werden (Horngren, C.T./Foster, G./Datar, S.M. 1997, S. 306 ff.). Bei stark abweichenden Datenkonstellationen muss das Modell revidiert werden. Dies kann bereits die Berechnung der Sicherheitsspanne erschweren.
3. Weitergehende Auswertungs- bzw. Anwendungsmöglichkeiten (Grundmodell und Varianten) a) Ein-Produkt-Unternehmen
Die BEP-Ermittlung ist ein erster Schritt im Kontext der Analyse der Planung, Steuerung und Kontrolle des Periodenerfolgs. Dabei wird unter anderem im Rahmen von BEA-Varianten hinterfragt, ob die prognostizierte Beschäftigung wohl zur Gewinnerzielung ausreichen wird und wie „ sicher “ dieses Ergebnis ist. Die Analyse des Einflusses von Mengenänderungen im Ein-Produkt-Unternehmen mündet in die zentrale Frage: „ Welche Mengen müssen mindestens verkauft werden, um alle Kosten zu decken? “ . Sie kann auf verschiedene Art gestellt und beantwortet werden (Coenenberg, A.G. 1999, S. 278 ff.):
| - | „ Welche Produktions- und Absatzmenge führt zur Deckung aller Ausgaben? “ Die Antwort gibt der Cash-Point. | | - | „ Welche Produktions- und Absatzmenge ist zur Erreichung eines Mindestgewinns erforderlich? “ Folglich ist Gleichung 1 nicht gleich Null, sondern gleich dem Mindestgewinn zu setzen, was faktisch der Berücksichtigung eines zusätzlichen Fixkostenblocks entspricht. | | - | „ Um welchen Prozentsatz darf die (absetzbare) Kapazitätsauslastung höchstens sinken, ohne dass ein Verlust entsteht? “ Diese Einschätzung ergibt sich aus dem Sicherheitskoeffizienten (vgl. Gleichung 4). | | - | „ Ist die (durch die Fixkosten repräsentierte) Kapazität in Bezug auf die Plan-Produktions- und -Absatzmenge angemessen? “ Dies wird zum Beispiel bejaht, wenn die Berechnung des sog. Kapazitätsgrads (KG) Werte von kleiner als eins ergibt. Der KG lässt sich zum Beispiel als Quotient aus dem planmäßigen Verhältnis aus Deckungsbeitragsvolumen (DBPlan) und Periodenfixkosten ermitteln: |
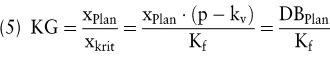 b) Mehr-Produkt-Unternehmen
BEA sind im Mehr-Produkt-Unternehmen nicht mehr eindeutig lösbar (Kilger, W. 1962, S. 95 ff.). Einen Ausweg bietet die Rückführung des Mehr-Produkt-Falls auf den Ein-Produkt-Fall. Zunächst muss der BEP wertmäßig als (kritischer) BEU definiert werden. Damit ist die Umsatzfunktion (im Umsatz-Gesamtkosten-Modell) auf der Winkelhalbierenden des ersten Quadranten abzutragen. Zudem sind feste Mengenrelationen der Produktarten zugrunde zu legen und auf die Zurechnung der Fixkosten auf einzelne Produktarten zu verzichten (sog. globale Fixkostenzurechnung). Die festen Mengenrelationen lassen die Deckungsbeitragskurve gemäß dem durchschnittlichen DBU-Faktor des Produktionsprogramms ansteigen und machen die Errechnung einer Produktmixabweichung bei nachträglichen Abweichungsanalysen notwendig (Schweitzer, M./Troßmann, E. 1998, S. 144 ff.).
Der Deckungsbeitragsgraph kann ceteris paribus auch durch eine fiktive Reihung der Produktarten nach abnehmenden (optimistische Variante; Mindest-BEU) oder zunehmenden DBU-Faktoren (pessimistische Variante; definitiver BEU) abgetragen werden (Anderson, L.K. 1975, S. 32; Ewert, R./Wagenhofer, A. 2000, S. 235 f.). Im Rahmen einer horizontalen Analyse lassen sich dann BEU-Spannen ermitteln, die in Verbindung mit Sicherheitsspannen/-koeffizienten das Risiko im weitesten Sinne erhellen sollen:

Ergänzend kann eine vertikale Analyse der einem BEU zuzuordnenden Deckungsbeitragsspannen erfolgen.
Obwohl weit verbreitet, ist das Reihungskriterium begründungsbedürftig. Es entspricht zum Beispiel nicht dem bei deckungsbeitragsmaximierendem Verhalten im Engpassfall maßgeblichen relativen Deckungsbeitrag je Engpassinanspruchnahme.
Varianten der BEA in Mehr-Produkt-Unternehmen sehen eine differenzierte Fixkostenzurechnung auf die Produktarten vor. Sie sind graphische Veranschaulichungen einer stufenweisen Fixkostendeckungsrechnung (Hahn, D. 1996, S. 400 ff.). Diese Gesamtkonzeption skizziert Abb. 2 bei vollständiger Zurechnung produktbezogener und anteiliger Zurechnung sonstiger Fixkosten. Hierin werden produktbezogene BEA in der Reihenfolge abnehmender DBU-Faktoren aneinander gelegt. Zudem enthält Abb. 2 eine rudimentäre Differenzierung des Fixkostenblocks von Produkt 1. Die in doppelten Linien gezeichneten Graphen repräsentieren die gesamtunternehmensbezogene Perspektive und führen zu alternativen BEU für das Gesamtunternehmen.
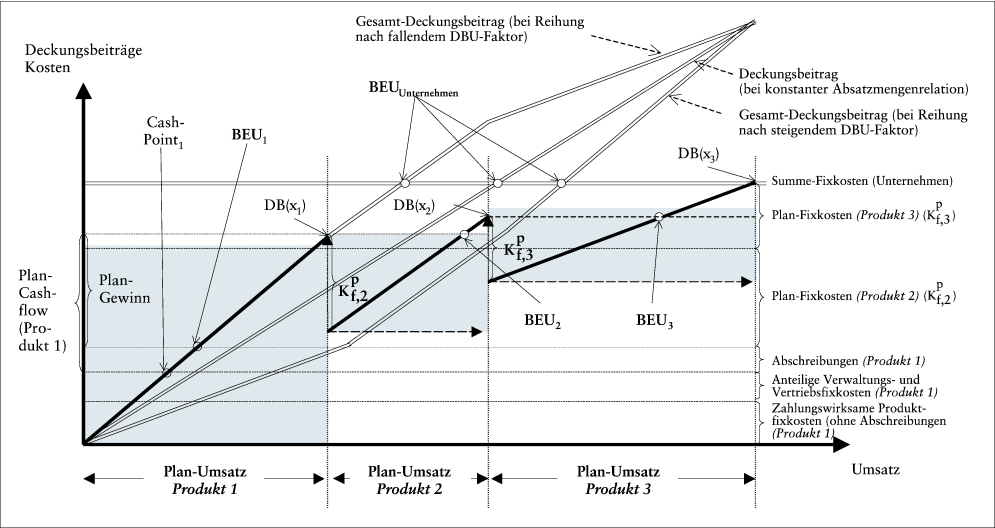
Abb. 2: Break-even-Analyse in einem Drei-Produkt-Unternehmen (Deckungsbeitrags-Modell)
III. Weitere Varianten der Break-even-Analyse
BEA-Varianten (vgl. Schirmeister, R. 2000; Tucker, S.A. 1980) ersetzen zum Beispiel die Umsatz- bzw. Erlösfunktion bei Auswahlentscheidungen im Produktionsbereich (Verfahrenswahl oder Rationalisierungsinvestitionen) oder im Absatzbereich (Reisende oder Vertreter) durch die Kostenfunktion der Alternative. Die Zielgröße muss nicht als kalkulatorischer Gewinn vor Steuern definiert werden. Stattdessen kann man auf eine Umsatzrentabilität (Chmielewicz, K. 1974), auf einen Gewinn nach Steuern (Morse, W.J./Posey, J.A. 1979/80) oder – wie im Rahmen einer externen BEA (Coenenberg, A.G. 2000, S. 1042 ff.; Haidacher, O.B. 1969, S. 84 ff.; Lorson, P. 1992) – auf einen pagatorischen Gewinn abstellen. Weiterhin lassen sich mengenunabhängige Erlöse berücksichtigen. Oder man rechnet zur Abbildung von Lagerbestandsänderungen in einem BEA-Modell den Fertigprodukten nur den absatzmengenbezogenen Anteil der produktionsbedingten Fixkosten zu (Schweitzer, M./Troßmann, E. 1998, S. 95 f.). Andere Anwendungen einer BEA sind schließlich nachträgliche Rechnungen zur Ermittlung absatzbezogener Risikomaße (Biermann, H.jr./Bononi, C.P./Hausman, W.H. 1981; Coenenberg, A.G. 1967): Sicherheitskoeffizient, Fehlentscheidungswahrscheinlichkeit, Risiko-Chance-Relation, erwartete Ungewissheitskosten und Risikograd.
IV. Erweiterungen der Break-even-Analyse
Hervorhebenswerte Richtungen der Erweiterung von BEA sind (Schweitzer, M./Troßmann, E. 1998, S. 122 ff.): mehrstufige, mehrdimensionale, dynamische, nichtlineare, stochastische und verschiedene Ziele berücksichtigende BEA. Mehrstufige BEA heben die Prämisse des einstufigen Produktionsprozesses auf. In Übereinstimmung mit realen Produktionstypen werden dann Zwischenerzeugnisproduktion und individuelle Kostenstrukturen der Produktionsstufen zugelassen. Zudem kann man Erlöse ohne Rückgriff auf Schlüssel allein den Enderzeugnissen zurechnen, wenn die Zwischenprodukte nicht über Verrechnungspreise zwischen den Produktionsstufen gehandelt werden (Lorson, P./Schweitzer, M. 2000, S. 323 ff.; Schweitzer, M./Troßmann, E. 1998, S. 173 ff.). Zur Illustration eines spezifischen Lösungskonzepts einer mehrstufigen BEA sei eine divergierende zweistufige Struktur angenommen. Auf der ersten Stufe wird ein Zwischenerzeugnis hergestellt, das den Input für die zweite Produktionsstufe darstellt, auf der programmbedingt zwei Enderzeugnisse gefertigt werden (Lorson, P./Schweitzer, M. 2000, S. 325): Die kritischen Mengen der Enderzeugnisse ergeben sich dann als Quotient der diesen zurechenbaren fixen Kosten (der zweiten Produktionsstufe; Kf,2_1 bzw. Kf,2_2) und dem Saldo aus Preis und der Summe von variablen Kosten der ersten (Zwischenerzeugnisfertigung; kv,1) und zweiten Produktionsstufe (Enderzeugnisfertigung; kv,2_1 bzw. kv,2_2):

Die Deckung der Fixkosten der ersten Produktionsstufe (Kf,1) erfordert die Erhöhung der Beschäftigungsmengen auf BEP1 = x1,krit bzw. BEP2 = x2,krit. Hierzu sind alle Mengenkombinationen der beiden Enderzeugnisse zulässig, die die nachstehende Gleichung mit nichtnegativen Werten lösen:
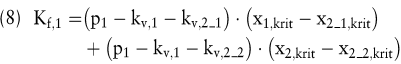
Mehrdimensionale BEA lösen sich von der Prämisse einer linearen Input-Output-Funktion mit konstantem Produktionskoeffizienten. Nun geht man von technischen Prozessfunktionen (Produktionsfunktionen) aus, die von zahlreichen Einflussfaktoren abhängen können (Schweitzer, M./Troßmann, E. 1998, S. 203 ff.). Die Bezeichnung nichtlineare BEA kennzeichnet den angenommenen nichtlinearen Verlauf der Kosten- und Erlösfunktionen aufgrund von sprungfixen Kosten, variierenden Stückkosten, Kostenremanenzen, mengenabhängigen Preisen usw. durch Rekurs auf Modelle der klassischen Preis- und Kostentheorie (Schweitzer, M./Troßmann, E. 1998, S. 284 ff.).
Dynamische BEA führen neben der Erfolgszielorientierung eine Zeitpräferenz ein. Bei der Berechnung der Gewinnschwelle kommt es nicht mehr nur allein auf die Höhe von (saldierten) Einnahmen oder Ausgaben an, sondern auch auf den Zeitpunkt ihres Anfalls. Im Ergebnis wird die Zeitspanne ermittelt, bis die kumulierten diskreten, zeitpunktbezogenen (gegebenenfalls diskontierten) Einnahmen die Ausgaben decken. Diese Amortisationsdauer wird durch Verzinsen regelmäßig beeinflusst (Weingartner, H.M. 1969), i.w.S. zum Beispiel bei einer unternehmenswertorientierten BEA. Unter die dynamische BEA kann man die Erstellung sog. BEP-Erreichungs-Chart (BEP-EC) subsumieren. Hierin werden (Teil-)Perioden auf der Abszisse und die BEP-Erreichung auf der Ordinate abgetragen. Dazu sind die für den Planungszeitraum prognostizierten Absatzmengen bzw. Umsätze Teilperioden zuzurechnen. Die vom Beginn der Planungsperiode an kumulierten Werte der Absatzmengen bzw. Umsätze bilden den Zähler der BEP-Erreichung zu einem bestimmten Zeitpunkt. Im Nenner sind dementsprechend xkrit bzw. BEUkrit zu berücksichtigen. Ein BEP-EC kann nebeneinander Graphen zur BEP-Erreichung im Plan und im Ist enthalten. Auftretende Abweichungen indizieren die Notwendigkeit einer Abweichungsauswertung.
Stochastische BEA berücksichtigen die Unsicherheit der Planung nicht wie bisher durch Sensitivitätsanalysen, sondern durch angenommene Wahrscheinlichkeitsverteilungen für bestimmte Plangrößen. Die Modelle reichen von der Ermittlung deterministischer BEP bis zu stochastischen BEP. Im ersteren Fall wird etwa allein die Absatzmenge als risikobehaftet angesehen und die Wahrscheinlichkeit des Verlassens der Verlustzone ermittelt. Komplexer sind stochastische Modelle, die von gegebenen Verteilungsfunktionen hinsichtlich der Eingangsgrößen Stückdeckungsbeitrag oder Fixkosten ausgehen (Bierman, H.jr. 1963; Jaedicke, R.K./Robichek, A.A. 1964; Schweitzer, M./Troßman, E. 1998, S. 203 ff.; Welzel, O. 1987). Sie sollen zum Beispiel durch Simulation die Wahrscheinlichkeitsverteilung von Gewinnfunktion bzw. BEP/BEU ermitteln und die Fragen „ Wie wahrscheinlich ist das Erreichen von BEP/BEU? “ oder „ Wie hoch ist der Periodenerfolg bei einer Wahrscheinlichkeit von x %? “ beantworten.
Die verschiedene Ziele berücksichtigende BEA kennt zwei Ausgestaltungsformen (Schweitzer, M./Troßmann, E. 1998, S. 336 ff.). Die erste ist auf Nicht-Gewinnziele ausgerichtet; die zweite auf die gleichzeitige Berücksichtigung mehrerer Ziele. Letztere Entwicklungsrichtung basiert auf Modellen der Linearen Optimierung (Charnes, A./Cooper, W.W./Ijiri, Y. 1963) oder des Multi-Goal-Programming bei Mehrfachzielsetzungen.
V. Zusammenfassende Würdigung
Die Logik der BEA ist bestechend. Allerdings leiden die sehr robusten, leicht zu handhabenden und schnell auszuwertenden Grundmodelle angesichts des Prämissenkorsetts unter einer Realitätsferne. Realitätsnähere Modelle sind aber komplexer und sensibler hinsichtlich der Qualität der Inputdaten. Dies spiegeln die Resonanz in der Unternehmenspraxis und Beurteilungen von BEA-Konzepterweiterungen im Schrifttum wider. Daher muss BEA-Anwendern in jedem Fall dazu geraten werden, flankierend andere geeignete Management-Instrumente zu nutzen.
Literatur:
Anderson, Lane K. : Expanded Break even Analysis for a Multi-Product Company, in: Management Accounting, Jg. 57, 1975, S. 30 – 32
Babbage, Charles : On the Economy of Machinery and Manufactures, London et al., 3. A., 1833
Bierman, Harold : Topics in Cost Accounting and Decisions, New York et al. 1963
Biermann, Harold jr./Bononi, Charles P./Hausman, Warren H. : Quantitative Analysis in Business Decisions, Homewood (Ill) et al., 6. A., 1981
Bücher, Karl : Das Gesetz der Massenproduktion, in: Zeitschrift für die gesamte Staatswissenschaft, Jg. 66, 1910, S. 429 – 444
Coenenberg, Adolf Gerhard : Jahresabschluß und Jahresabschlußanalyse, Landsberg am Lech, 17. A., 2000
Coenenberg, Adolf Gerhard : Kostenrechnung und Kostenanalyse, Landsberg am Lech, 4. A., 1999
Coenenberg, Adolf Gerhard : Die Berücksichtigung des Absatzrisikos im Break-even-Modell, in: BFuP, Jg. 19, 1967, S. 343 – 355
Charnes, Abraham/Cooper, William W./Ijiri, Yuji : Break-even Budgeting and Programming to Goals, in: JAR, Jg. 1, 1963, S. 16 – 43
Chmielewicz, Klaus : Gewinnschwellenanalyse (Break-even-Analyse), in: Wirtschaftswissenschaftliches Studium, Jg. 3, 1974, S. 49 – 54
Dammann, Winfried : Break-even-Analyse: Ein Instrument der Gewinnplanung, in: KRP, 1963, S. 111 – 119
Dean, Joel : Capital Budgeting, New York/London, 8. A., 1969
Dean, Joel : Methods and Potentialities of Break Even-Analysis, in: Studies in Costing, hrsg. v. Solomons, D., London 1952, S. 227 – 266
Ewert, Ralf/Wagenhofer, Alfred : Interne Unternehmensrechnung, Berlin et al., 4. A., 2000
Hahn, Dietger : PuK – Controllingkonzepte, Wiesbaden, 5. A., 1996
Haidacher, Oskar B. : Der Break-even-Punkt als Instrument unternehmerischer Führung, München 1969
Hess, H. : Manufacturing: Capital, Costs, Profits, and Dividends, in: The Engineering Magazine, 1903/1904, Bd. 26, S. 367 – 379
Horngren, Charles T./Foster, George/Datar, Srikant M. : Cost Accounting, Upper Saddle River, New Jersey et al., 9. A., 1997
Jaedicke, Robert K./Robichek, Alexander A. : Cost-Volume-Profit Analysis under Conditions of Uncertainty, in: Acc.R, Jg. 39, 1964, S. 917 – 926
Kilger, Wolfgang : Kritische Werte in der Investitions- und Wirtschaftlichkeitsrechnung, in: ZfB, Jg. 35, 1965, S. 338 – 353
Kilger, Wolfgang : Kurzfristige Erfolgsrechnung, Wiesbaden 1962
Kleinebeckel, Herbert : Break-even-Analysen, in: ZfbF (Teil 1), Jg. 28, 1976, S. 51 – 58
Kleinebeckel, Herbert : Break-even-Analysen, in: ZfbF (Teil 2), Jg. 28, 1976, S. 117 – 124
Knoeppel, Charles Eduard : Profit Engineering, New York et al. 1933
Knoeppel, Charles Eduard/Seybold, Edgar G. : Managing for Profit: Working Methods for Profit Planning and Control, New York 1937
Lardner, Dionysius : Railway Economy: A Treatise on the New Art of Transport, its Management, Prospects, and Relations, Commercial, Financial and Social, London et al. 1850
Lorson, Peter : Möglichkeiten und Grenzen der Break-Even-Analyse als Instrument der Betriebsanalyse, in: Deutsches Steuerrecht, Jg. 30, 1992, S. 300 – 307
Lorson, Peter/Schweitzer, Marcus : Kostenrechnung, in: Saarbrücker Handbuch der betriebswirtschaftlichen Beratung, hrsg. v. Küting, Karlheinz, Herne/Berlin, 2. A., 2000, S. 233 – 373
Mann, John : Oncost or Expenses, in: Encyclopaedia of Accounting, Bd. V, hrsg. v. Lisle, George, Edinburgh et al. 1904, S. 199 – 223
Morse, Wayne J./Posey, Imogene A. : Income Taxes Do Make a Difference in C-V-P Analysis, in: Management Accounting, Jg. 61, Dezember/1979/80, S. 20 – 24
Rautenstrauch, Walter : The successful Control of Profits, New York 1930
Schär, Johann Friedrich : Allgemeine Handelsbetriebslehre, Bd. 1, Leipzig 1911
Schirmeister, Raimund : Break-even-Analyse, in: Kosten-Controlling, hrsg. v. Fischer, Thomas M., Stuttgart 2000, S. 207 – 234
Schweitzer, Marcell/Troßmann, Ernst : Break-even-Analysen, Berlin, 2. A., 1998
Tucker, Spencer A. : Profit Planning Decisions with the Break-Even-System, New York, 2. A., 1980
Weingartner, H. Martin : Some New Views on the Pay back Period and Capital Budgeting Decisions, in: Management Science, Jg. 15, 1969, S. B 594 – B 607
Welzel, Otmar : Möglichkeiten und Grenzen der stochastischen Break even-Analyse als Grundlage von Entscheidungsverfahren, Heidelberg 1987
Williams, J.H. : A technique for the Chief Officer, in: Bulletin of the Taylor Society, New York, Jg. 7, 1922, S. 47 – 68
|