|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||
Die (im Falle einer Risikosituation bekannten)
Zustandswahrscheinlichkeiten bezeichnen wir mit p1,p2,?, wobei
pi = P (Zustand zi tritt ein).
Im Falle eines kontinuierlichen Zustandsraumes ist anstelle
der Zustandswahrscheinlichkeiten natürlich eine Wahrscheinlichkeitsdichte zu
verwenden.
2. Mischformen zwischen Risikosituationen und
Ungewissheitssituationen
Mischformen entstehen, wenn Zustandswahrscheinlichkeiten nur
unzureichend bekannt sind. Dies kann mehrere Ursachen haben. Betrachten wir zur
Erläuterung der ersten Ursache einen zweielementigen Zustandsraum Z = {z1,z2} wie etwa im
Kreditnehmer-Beispiel des vorangegangenen Abschnitts. Ist hierfür nur bekannt,
dass der Zustand z1 mindestens so wahrscheinlich wie der Zustand z2 ist, so liegt zwar eine verlässliche Angabe
oder Restriktion p1 ≥ p2 bzgl. der Zustandswahrscheinlichkeiten
vor. Die Angabe ist jedoch zu rudimentär,
um die für eine Risikosituation benötigte Zustandsverteilung eindeutig
festzulegen. So sind im Rahmen der Angabe beispielsweise die
Zustandsverteilungen
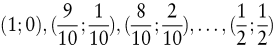
sowie (unendlich) viele weitere Verteilungen möglich. Das
Analoge gilt auch bei Angaben vom Typus
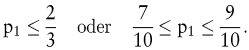
Bei mehr als zwei Zuständen wird die Vielfalt von denkbaren
Restriktionen und damit verträglichen Zustandsverteilungen naturgemäß noch viel
größer. Können alle Restriktionen in Form von linearen Gleichungen und
Ungleichungen formuliert werden, so liegt eine lineare partielle Information
(LPI) vor. (Wegen derartiger Modelle sei beispielsweise auf Kofler,
E./Menges, G. 1976; Kofler, E.
1989; Bamberg,
G./Coenenberg, A.G. 2000 verwiesen.)
Neben dem Vorliegen von handfesten aber zu rudimentären
Informationen bzgl. der Zustandsverteilung sei noch eine weitere Ursache
für Mischformen betrachtet. Sie liegt in den Schwierigkeiten begründet, die
reale Entscheidungsträger mit der Wahrnehmung und Handhabung von
Wahrscheinlichkeitsverteilungen haben. So könnte (vielleicht aufgrund
mangelnder Recherchen oder Phantasie) eine Gleichverteilung über alle Zustände
für möglich erachtet werden, ohne dass der Entscheidungsträger sonderlich davon
überzeugt ist, dass dies die „ wahre Zustandsverteilung “ ist. Dann liegt zwar
eine eindeutige, gleichzeitig aber wenig
vertrauenswürdige Zustandsverteilung vor. In der Entscheidungstheorie
wurden auch hierauf zugeschnittene Entscheidungsregeln entwickelt, wie etwa die
Hodges-Lehmann-Regel (vgl. Mag, W.
1990). An dieser Stelle könnte man sich zu Recht fragen, ob zwischen objektiven
und subjektiven Wahrscheinlichkeiten nicht strenger unterschieden werden
sollte. Objektive Wahrscheinlichkeiten treten bei klassischen Glücksspielen
(Lotto, Roulette u. dgl.) auf und können mithilfe von Symmetrien, Annahmen über
die Ordnungsmäßigkeit von Geräten usw. deduziert werden. Die meisten ökonomisch
relevanten Situationen sind jedoch nicht von diesem Typus. Selbst in der
Lebensversicherung, in der man es mit beeindruckend vielen empirischen Daten zu
tun hat, ist es unmöglich, aufgrund der heutigen Sterbetafeln die objektiven
Sterbewahrscheinlichkeiten für aktuell gewonnene Versicherungsnehmer zu
deduzieren. In aller Regel sind die bei praxisrelevanten Entscheidungssituationen
verwendeten Wahrscheinlichkeiten stets in einem mehr oder minder großen Maße
subjektiv, auch wenn noch so viele empirische Daten oder Expertenmeinungen die
Festlegung bzw. Schätzung der Wahrscheinlichkeiten stützen. Deshalb werden
in der Entscheidungstheorie gleichermaßen subjektive wie objektive
Wahrscheinlichkeiten benutzt.
Die mangelnde Verarbeitungskapazität von Wahrscheinlichkeiten
durch reale Entscheidungsträger verursacht einen weiteren Effekt, der zu
Mischformen Anlass gibt. Es handelt sich um den Ambiguitäts-Effekt, gemäß dem
in verschiedenen Situationen, die vom wahrscheinlichkeitstheoretischen
Standpunkt aus äquivalent sind, diejenigen bevorzugt werden, bei denen sich der
Entscheidungsträger ein klareres Bild von den Wahrscheinlichkeiten machen kann.
In einer experimentellen Untersuchung hat Weber (Weber, M.
1989) den Ambiguitäts-Effekt in Finanz- und Kapitalmärkten nachgewiesen.
3. Maßnahmen zur Verbesserung des
Informationsstandes
Eine Verbesserung des Informationstandes erfordert im
allgemeinen Zeit, Mühen und Geld. Mithilfe des Begriffs des Informationswertes,
der in vielen entscheidungstheoretischen Lehrbüchern (z.B. Dinkelbach,
W. 1982; Mag, W.
1990; Laux, H.
1998; Bamberg,
G./Coenenberg, A.G. 2000) behandelt wird, kann man entscheiden, ob
sich die (mit Kosten verbundene) Inanspruchnahme einer Informationsquelle lohnt
oder nicht lohnt. Mit demselben Begriff kann man auch das Problem lösen, aus
verschiedenen konkurrierenden Informationsquellen die beste herauszusuchen.
II. Entscheidungen bei
Risiko
Im Gegensatz zu Kapitel I soll die Wahrscheinlichkeitsverteilung
der Zustände nicht weiter problematisiert werden. Interessanterweise treten
nämlich die Schwierigkeiten, die mit verschiedenen Lösungskonzepten und
Entscheidungsregeln verbunden sind, auch dann schon auf, wenn rein objektive,
d.h. aus den Axiomen der Wahrscheinlichkeitstheorie ableitbare,
Zustandswahrscheinlichkeiten gegeben sind. Dann ist auch für jede Aktion
a,b,c,? eine Zufallsvariable Xa,Xb, Xc,? festgelegt, deren Realisation mit dem
jeweiligen Ergebnis der Aktion bei dem realisierten Zustand identisch ist.
Aktion a →
Zufallsvariable Xa
Zur Illustration sei beispielsweise die Aktion
betrachtet. Vereinfachend werde ein vierelementiger
Zustandsraum Z = {z1,z2,z3,z4} angenommen
mit
z1/2/3/4 = Kassakurs am
Ultimo ist 65, – /70, – /75, – /80, –
Die Zustandswahrscheinlichkeiten seien
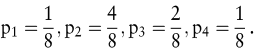
Schließlich sei als Ergebnis der Aktion der jeweilige Gewinn
unter Vernachlässigung von Transaktionskosten und Steuern verstanden.
Infolgedessen entspricht a der Zufallsvariablen Xa
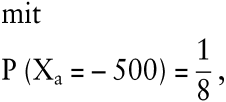
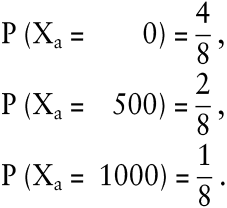
1. Klassische Entscheidungsprinzipien
Die Wahl zwischen zwei risikobehafteten Entscheidungen a und
b entspricht also der Wahl zwischen den beiden zugehörigen Zufallsvariablen Xa und Xb. Die klassischen
Entscheidungsprinzipien postulieren, dass für die Präferenz bzw. Indifferenz
zwischen zwei Zufallsvariablen nicht die gesamte Wahrscheinlichkeitsverteilung,
sondern nur einige wenige Verteilungskennzahlen maßgeblich sind. Spielt nur der
Erwartungswert μ eine Rolle, so spricht man vom μ-Prinzip. Das
prominenteste klassische Entscheidungsprinzip besagt jedoch, dass sowohl der
Erwartungswert μ als auch die Standardabweichung σ für die Bestimmung
der Rangfolge zwischen den Aktionen relevant sind. Dementsprechend heißt das
Prinzip auch das (μ, σ)-Prinzip.
In Anbetracht der vielen weiteren denkbaren
Verteilungsparameter (Median, Modalwert, Schiefe, Wölbung,
Verlustwahrscheinlichkeit, Verlusterwartungswert, Semivarianz, Spannweite, Risikomaße,
Minimum, Maximum usw.) sowie der Möglichkeit, diese allein zu betrachten, zu
Gruppen von je zwei, je drei,? zusammenzufassen, erkennt man, dass es so viele
klassische Entscheidungsprinzipien gibt, wie die Phantasie reicht. Hinzu kommt
noch ein weiterer Spielraum für die Phantasie. Denn die Zugrundelegung eines
klassischen Entscheidungsprinzips setzt nur einen Rahmen. Eine definitive
Rangfolge der zur Debatte stehenden Aktionen erhält man erst, wenn genau
festgelegt ist, wie die relevanten Verteilungsparameter zu einer
Bewertungsziffer kombiniert werden. Erst diese letztere Festlegung macht aus
dem Entscheidungsprinzip eine
Entscheidungsregel. Betrachten wir
dazu wieder das (μ,σ)-Prinzip und bezeichnen wir die gemäß der
jeweiligen Entscheidungsregel gebildete Bewertungs- oder Güteziffer mit
Φ(μ,σ), so sind beispielsweise Φ(μ,σ) = μ-
0,15 ·σ oder Φ(μ,σ) = μ – 0,03 ·σ2 denkbare Entscheidungsregeln. Gilt für die
Ergebnisse der risikobehafteten Aktionen „ je größer, desto besser “ , was bei
Renditen, Gewinnen, Endvermögen usw. zutrifft, so sollte eine plausible
(μ,σ)-Regel die Eigenschaften haben, daß Φ(μ,σ)
monoton mit μ steigt und mit σ fällt.
Die zweite Eigenschaft drückt Risikoaversion des
Entscheidungsträgers aus. Beim Vergleich einer Zufallsvariablen X mit dem
sicheren Ergebnis in Höhe von μ = E(X) präferiert er Letzteres: E(X) X.
Denn die sichere Alternative hat die Bewertungsziffer
Φ(μ,0), wohingegen X nur die kleinere Bewertungsziffer
Φ(μ,σ) besitzt. Obige (μ,σ)-Regeln erfüllen beide
Plausibilitätsforderungen. Man wird sich häufig für das sichere Ergebnis s
interessieren, sodass der Entscheidungsträger indifferent zwischen s und X ist:
s ~ X. Dieses s bezeichnet man als Sicherheitsäquivalent von X. Risikoaversion
liegt demnach vor, wenn das Sicherheitsäquivalent kleiner als E(X) ist; der
Entscheidungsträger gibt sich mit einem Ergebnis zufrieden, das kleiner als der
Erwartungswert ist. Gilt umgekehrt s > E(X), so bezeichnet man das Verhalten
als risikofreudig. Gilt schließlich stets s = E(X), so liegt Risikoneutralität
vor. In der Portfoliotheorie
müssen risikofreudige (sowie risikoneutrale) Akteure aus folgendem Grunde
ausgeklammert werden: Existieren beispielsweise eine risikobehaftete
Anlagemöglichkeit mit einer erwarteten Rendite von 10% und ein risikofreier
Zinssatz von 8% (zu dem beliebige Beträge ge- oder verliehen werden können), so
würde ein risikofreudiger oder risikoneutraler Investor einen beliebig hohen
Kredit aufnehmen und das Geld risikobehaftet anlegen. Es gäbe mithin weder eine
optimale Kombination von risikobehafteter und risikofreier Anlage noch ein
Kapitalmarktgleichgewicht. Bei risikoaversen Investoren existieren keine
derartigen Probleme. Das optimale Portfolio kann im Prinzip einfach bestimmt
werden; eine graphische Darstellung ist in Abb. 1 zu finden. In der
Abbildung wurden ausschließlich risikobehaftete Portfolios berücksichtigt.
Wegen der vielfältigen Ergänzungen (risikofreie Anlage, Leerverkäufe,
differierender Soll- und Habenzins usw.) sei auf Standard-Lehrtexte zur Finanz-
und Kapitalmarktheorie verwiesen (beispielsweise auf Uhlir,
H./Steiner, P. 1994; Spremann, K.
1996; Kruschwitz,
L. 1999; Franke,
G./Hax, H. 1999; Perridon,
/Steiner, 1999).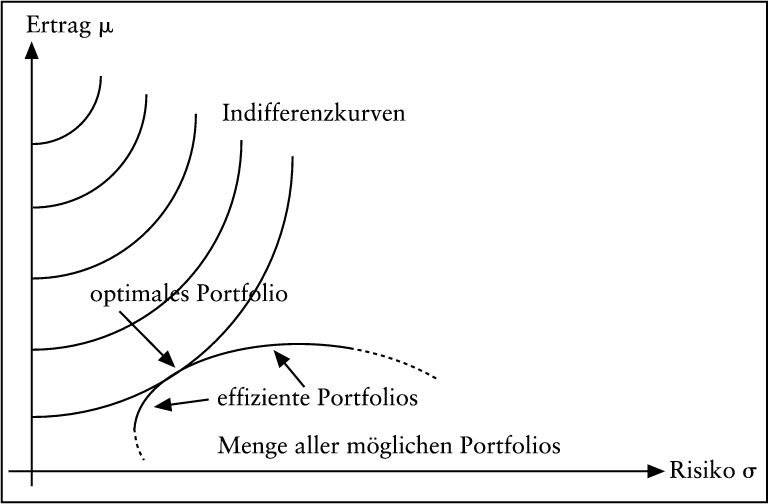
Abb. 1: Jedem Portfolio entspricht ein Punkt der
(σ,μ)-Ebene. Der Tangentialpunkt der Effizienzkurve mit einer
Indifferenzkurve bestimmt das optimale Portfolio.
2. Das Bernoulli-Prinzip
Bei der Diskussion der klassischen Entscheidungsregeln wurde
auf den großen Spielraum (bzw. die Willkür) bei der Fixierung einer Regel
hingewiesen. Trotz dieses Spielraumes ist jede der auswählbaren Entscheidungsregeln
mit einer relativ großen Inflexibilität behaftet. So müssen bei einer
(μ,σ)-Regel Ergebnisverteilungen zwangsläufig als gleichwertig
gelten, wenn sie in Bezug auf diese beiden Parameter übereinstimmen. Man kann
leicht Beispiele konstruieren, bei denen diese Indifferenz weder plausibel noch
empirisch gestützt ist.
Das Bernoulli-Prinzip besitzt diesen Mangel an Flexibilität
nicht, da es die Ergebnisverteilung in ihrer Gesamtheit einbezieht. Es ist nach
Daniel Bernoulli benannt, der bereits 1738 zutreffend erkannt hatte, dass die
alleinige Orientierung am Ergebniserwartungswert reales Verhalten nicht adäquat
beschreibt und dass eine für den Entscheidungsträger typische Einstellung zum
Risiko mit einbezogen werden muss. Das Bernoulli-Prinzip (im Englischen
„ expected utility hypothesis “ ) besagt:
Es gibt für jeden
Entscheidungsträger eine (auf der Menge aller Ergebnisse definierte und bis auf
eine wachsende lineare Transformation eindeutige) Nutzenfunktion u mit der
Eigenschaft, dass die verschiedenen Aktionen aufgrund des zugehörigen
Nutzenerwartungswertes beurteilt werden.
Die nachfolgenden Bemerkungen sollen diese abstrakt wirkende
Aussage kommentieren und verständlicher machen.
a) Sind Xa und Xb die zu den risikobehafteten Aktionen a und b
gehörenden Zufallsvariablen, so besagt das Bernoulli-Prinzip
a ≻ b genau dann wenn E u(Xa) > E u(Xb),
a ~ b genau dann wenn E u(Xa) = E u(Xb);
d.h. die Bewertungsfunktion Φ, die jeder Aktion a
eine Güteziffer zuordnet, besitzt beim Bernoulli-Prinzip die Form
Φ(a) = E u(Xa).
b) Betrachten wir beispielsweise die eingangs dieses Kapitels
präzisierte Aktion a (= Kauf von 100 DaimlerChrysler-Aktien und Verkauf zum
Jahresultimo), so bestimmt sich der Nutzenerwartungswert gemäß
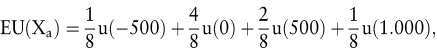
was sich bei konkret gegebener Funktion u unschwer als reelle
Zahl ausrechnen lässt.
c) Die im Vergleich zu den klassischen
Entscheidungsprinzipien erhöhte Flexibilität entsteht dadurch, dass jedes
einzelne Ergebnis x in eine (subjektive) Größe u(x) transformiert werden kann.
Es mag der Verdacht aufkommen, dass es sich beim Bernoulli-Prinzip infolge
dieser großen Flexibilität um ein tautologisches Konzept handeln könnte. Dass
dies nicht der Fall ist, zeigen Beispiele, bei denen die vom
Entscheidungsträger geäußerte Präferenz zwischen risikobehafteten Aktionen dem
Bernoulli-Prinzip widersprechen kann. Geht man andererseits von der Gültigkeit
des Bernoulli-Prinzips aus, so lässt sich aus dem Verhalten von
Entscheidungsträgern in sehr einfach strukturierten Entscheidungssituationen
die Funktion u empirisch ermitteln. Wegen Details sei auf die Literatur
verwiesen (beispielsweise auf Bitz, M.
1981; Schneeweiß,
Ch. 1991; Bamberg,
G./Coenenberg, A.G. 2000).
d) Das Bernoulli-Prinzip kann aus einigen
Rationalitätspostulaten (für die Präferenzordnung zwischen den
Zufallsvariablen) gefolgert werden. Einige Postulate sind vom normativen
Standpunkt aus sehr natürlich und fast zwingend. Einige andere sind umstritten
und haben einen geringeren normativen Gehalt. Wiederum sei auf die eben
zitierte Literatur verwiesen.
e) Ist die Bernoulli-Nutzenfunktion u streng monoton wachsend
und stetig, so kann das Sicherheitsäquivalent s folgendermaßen dargestellt
werden:
s = u – 1 [E u(X)].
f) Als (lokale) Maßzahl für den Grad der Risikoaversion wird
im Rahmen des Bernoulli-Prinzips das Arrow-Pratt-Maß
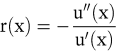
verwendet. Es ist positiv für risikoaverse, negativ für risikofreudige
und gleich Null für risikoneutrale Entscheidungsträger. Je größer die Funktion
r(x) ist, desto größer ist der Unterschied zwischen E(X) und dem
Sicherheitsäquivalent s und damit die als Risikoprämie bezeichnete Differenz
E(X) – s. Für risikoneutrale Entscheidungsträger ist die Risikoprämie gleich
Null.
g) In den Journalen „ Zeitschrift für Betriebswirtschaft “ und
„ Zeitschrift für betriebswirtschaftliche Forschung “ , neuerdings auch in der
„ Betriebswirtschaftlichen Forschung und Praxis “ sowie dem „ OR Spektrum “ , fanden
verschiedene Diskussionsrunden statt, wobei es um die Sinnhaftigkeit des
Bernoulli-Prinzips, die Interpretation von u und schließlich um den
Zusammenhang von u(x) mit den Werten h(x) der (ohne Bezugnahme auf
Risikoaspekte) auf den Ergebnissen x definierten kardinal messenden
Höhenpräferenzfunktion h ging. Die Kritiker des Bernoulli-Prinzips verfochten
den Standpunkt, dass aus logischen Gründen u(x) = h(x) gelten muss. Definiert
man die Ergebnisse richtig, d.h. als h(x) und nicht als x, so reduziert
sich der Nutzenerwartungswert des Bernoulli-Prinzips auf den schlichten
Erwartungswert der (richtig aufgefassten) Ergebnisse. Infolgedessen ist das
Bernoulli-Prinzip nicht in der Lage, verschiedene Einstellungen gegenüber dem
Risiko zu erfassen. Vielmehr kann es nur Risikoneutralität ausdrücken und ist
damit unflexibler als die meisten klassischen Prinzipien. Die „ Kritiker der
Kritiker “ wiesen jedoch nach, dass u(x) = h(x) nicht aus logischen Gründen
zwingend folgt. Deshalb kann das Bernoulli-Prinzip sehr wohl eine breite
Palette unterschiedlicher Einstellungen gegenüber dem Risiko abbilden. (Wegen
einer ausführlichen Darstellung dieser Diskussion sei verwiesen auf Kürsten, W.
1992; Dyckhoff, H.
1993; Bamberg,
G./Coenenberg, A.G. 2000.)
3. Weitere Entscheidungsprinzipien bei Risiko
Wohl bei jedem Entscheidungsprinzip kann man geeignete Situationen
konstruieren, in der die Mehrzahl der Entscheidungsträger gegen das auf dem
Prüfstand befindliche Prinzip verstoßen. Auch beim Bernoulli-Prinzip hat es
seit der in den frühen 1950er-Jahren von Allais
vorgebrachten Kritik nicht an derartigen Versuchen gemangelt (Allais, M.
1953). Diese Experimente gaben oft den Anstoß für alternative Theorien, für die
allerdings auch wieder empirische oder theoretische Kritikpunkte gefunden
wurden. Relativ bekannt wurden die „ duale Theorie “ sowie die „ rank dependent
expected utility “ -Theorie. (Wegen einer ausführlichen Darstellung sei
beispielsweise auf Weber,
M./Camerer, C. 1987; und Trost, R.
1991 verwiesen.)
III. Entscheidungen bei
Ungewissheit
Wenn keine Wahrscheinlichkeiten für die „ Kalkulation des
Risikos “ zur Verfügung stehen, bleiben im Wesentlichen nur die beiden
Möglichkeiten,
a) die effizienten Aktionen auszusondern und als
gleichwertige Lösungen zu offerieren;
b) mittels einer speziellen Entscheidungsregel alle Aktionen
in einer Rangfolge zu bringen (und damit auch „ den Spitzenreiter “ zu
identifizieren).
Dabei heißt eine Aktion effizient,
wenn keine der restlichen Aktionen bzgl. aller Zustände mindestens so gut
und bzgl. eines Zustands (oder auch mehrerer Zustände) besser ist als die
fragliche Aktion. Es sei wieder das Eingangsbeispiel von Kapitel II betrachtet.
Die Aktion a (Kauf von 100 DaimlerChrysler-Aktien) wird nun als a1 bezeichnet. Zusätzlich seien
Damit erhält man die Entscheidungsmatrix
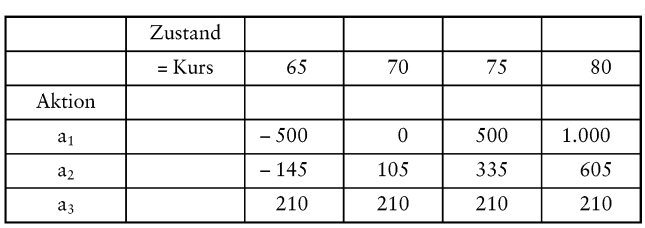
aus der man ersieht, dass alle drei Aktionen effizient sind.
Bezeichnen wir zur Darstellung der exemplarisch betrachteten
Entscheidungsregeln die Elemente der Entscheidungsmatrix mit uij, so ist die
Maximin-Regel durch die Bewertung
Φ (ai) = min uij
j
definiert, die Maximax-Regel durch
Φ (ai) = max uij,
j
die Hurwicz-Regel mit dem Optimismus-Parameter
λ ∊ [0,1] durch
Φ (ai) = λ max uij + (1-λ) min uij,
j j
sowie die Savage-Niehans-Regel durch die (zu minimierende)
Bewertungsziffer
Φ (ai) = max (max ukj – uij) .
j k
Eine ausführliche Diskussion des Pro und Contra sowie weitere
Regeln sind in der Literatur zu finden (beispielsweise in Bitz, M.
1981; Dinkelbach,
W. 1982; Mag, W.
1990; Laux, H.
1998; Homburg, C.
2000; Bamberg,
G./Coenenberg, A.G. 2000). Für unser Beispiel ersieht man, dass a1 optimal bzgl. der Maximax-Regel sowie
bzgl. der Hurwicz-Regel mit Optimismus-Parameter λ = 0,5 ist. Bezüglich
der Savage-Niehans-Regel ist dagegen a2 optimal. Schließlich ist a3 optimal bzgl. der Maximin-Regel.
Literatur:
Allais, M. : Le comportement de l\'homme
rationel devant le risque: Critique des postulats et axiomes de l\'école
américaine, Econometrica 21, 1953, S. 503 – 546
Bamberg, G. : Statistische
Entscheidungstheorie, Würzburg/Wien 1972
Bamberg, G./Coenenberg, A.G. :
Betriebswirtschaftliche Entscheidungslehre, 10. A., München 2000
Bitz, M. : Entscheidungstheorie, München
1981
Dinkelbach, W. : Entscheidungsmodelle,
Berlin/New York 1982
Dyckhoff, H. : Ordinale versus kardinale
Messung beim Bernoulli-Prinzip: Eine Analogiebetrachtung von Risiko- und
Zeitpräferenzen, OR Spektrum 15, 1993, S. 139 – 146
Franke, G./Hax, H. : Finanzwirtschaft des
Unternehmens und Kapitalmarkt, 4. A., Berlin et al. 1999
Homburg, C. : Quantitative
Betriebswirtschaftslehre, 3.A., Wiesbaden 2000
Kofler, E. : Prognosen und Stabilität bei
unvollständiger Information, Frankfurt/New York 1989
Kofler, E./Menges, G. : Entscheidungen
bei unvollständiger Information, Berlin et al. 1976
Kruschwitz, L. : Finanzierung und
Investition, 2. A., München/Wien 1999
Kürsten, W. : Präferenzmessung,
Kardinalität und sinnmachende Aussagen, ZfB 62, 1992, S. 459 – 477
Laux, H. : Entscheidungstheorie,
4. A., Berlin et al. 1998
Mag, W. : Grundzüge der
Entscheidungstheorie, München 1990
Perridon, L./Steiner, M. :
Finanzwirtschaft der Unternehmung, 10. A., München 1999
Schneeweiß, Ch. : Planung I, Berlin et
al. 1991
Schneeweiß, Ch. : Planung II, Berlin et
al. 1992
Schneeweiß, H. : Entscheidungskriterien
bei Risiko, Berlin et al. 1967
Schneider, D. : Investition, Finanzierung
und Besteuerung, 7. A., Wiesbaden 1992
Spremann, K. : Wirtschaft, Investition
und Finanzierung, 5. A., München/Wien 1996
Trost, R. : Entscheidungen unter Risiko:
Bernoulli-Prinzip und duale Theorie, Frankfurt a.M. et al. 1991
Uhlir, H./Steiner, P. :
Wertpapieranalyse, 3. A., Berlin/New York 1994
Weber, M. : Ambiguität in Finanz- und
Kapitalmärkten, ZfbF 41, 1989, S. 447 – 471
Weber, M./Camerer, C. : Recent
Developments in Modelling Preferences under Risk, OR-Spektrum 9, 1987,
S. 129 – 151
Wilhelm, J. : Zum Verhältnis von
Höhenpräferenz und Risikopräferenz – eine theoretische Analyse, ZfbF 38, 1986,
S. 467 – 492
copyright © www.dasWirtschaftslexikon.com 2012 Datenschutzbestimmungen Impressum Nutzungsbedingungen
| | | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
copyright © www.dasWirtschaftslexikon.com 2012 Datenschutzbestimmungen Impressum Nutzungsbedingungen |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| | | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Weitere Begriffe : Rendite | Lernen | Wertpapierbörse