|
Portfoliotheorie, finanzwirtschaftliche
Inhaltsübersicht
I. Einleitung
II. Das Entscheidungsproblem des Investors
III. Präferenzen im Erwartungswert/Varianz-Raum
IV. Effiziente Portfolios
V. Erweiterungen der Portfoliotheorie
VI. Grenzen der Portfoliotheorie
I. Einleitung
Die Portfoliotheorie kann als einer der wesentlichen Meilensteine auf dem Weg zu einer geschlossenen, mikroökonomisch fundierten Finanzierungstheorie angesehen werden. Sie basiert auf den Arbeiten von Harry Markowitz (Markowitz, 1952; Markowitz, 1959). Andere frühe, aber bei weitem nicht so rigorose Ansätze entwickelten Roy (Roy, A. 1952) und Freund (Freund, R. 1956).
Ursprünglich verfolgte Markowitz die Intention, eine normative Theorie im Sinne von Handlungsempfehlungen für Investoren zu entwickeln. Sein Ansatz löste das bis dahin eher diffuse Verständnis von Diversifikation und Portfolio-Bildung (\'Don\'t put all your eggs in one basket\') ab. Als Grundlage hierfür diente die erstmalige explizite Abbildung der Substitutionsbeziehung zwischen Rendite und Risiko einer Kapitalanlage. Darüber hinaus bildet die Portfoliotheorie die Basis für die Modellierung von Gleichgewichtsprozessen auf dem Kapitalmarkt (z.B. Sharpe, W. F. 1964) und erlangt dadurch auch aus positivistischer Sicht einen herausragenden Stellenwert. Die Bedeutung der Portfoliotheorie und ihrer Weiterentwicklungen wurde 1990 mit der Vergabe des Nobelpreises für Wirtschaftswissenschaften an Markowitz und Sharpe (zusammen mit M. H. Miller, ) gewürdigt.
Das zu seiner Zeit revolutionäre Konzept effizienter Portfolios beruht auf der Annahme, dass sich die relative Vorteilhaftigkeit von Kapital-Anlagen hinreichend durch die beiden ersten zentralen Momente ihrer Renditeverteilung, Mittelwert und Varianz, beschreiben lässt. Ein Portfolio wird als effizient bezeichnet, falls kein anderes Portfolio bei gleicher Rendite-Varianz eine höhere erwartete Rendite aufweist. Ein den Erwartungsnutzen maximierender Investor sollte ausschließlich aus der Menge effizienter Portfolios das für ihn optimale Portfolio auswählen. Tobin (Tobin, J. 1958) erweiterte den Ansatz, indem er nachwies, dass die optimale Mischung risikobehafteter Kapitalanlagen bei Existenz einer risikolosen Kapitalanlage unabhängig von der lokalen Risikoaversion, also vom Vermögen des Investors ist. Diese Separations-Eigenschaft hat weitreichende Implikationen im Marktzusammenhang. Bei Homogenität der Erwartungen halten alle Marktteilnehmer im Gleichgewicht das gleiche Portfolio risikobehafteter Kapitalanlagen. Für dieses sogenannte Marktportfolio existiert ein einheitlicher Marktpreis des Risikos, der die Berechnung intersubjektiver Risikoprämien ermöglicht. Auf Basis dieser Überlegungen wurde die Preis-Relation des Capital Asset Pricing Model (CAPM) von Sharpe (Sharpe, W. F. 1964) entwickelt. Ausgehend vom CAPM wird der renditegenerierende Prozess einer Kapitalanlage als lineares Modell (Markt-Modell) beschrieben. Durch die Separierbarkeit des Gesamtrisikos einer Anlage in systematische und unsystematische Bestandteile lässt sich der Aufwand zur Bestimmung effizienter Portfolios stark reduzieren, was den Einsatz der Portfoliotheorie in der Praxis erleichtert.
II. Das Entscheidungsproblem des Investors
Ausgangspunkt der Portfoliotheorie ist der normative Anspruch, dem Investor die Wahl eines optimalen Portfolios zu ermöglichen. Es wird unterstellt, dass die Entscheidungsträger den Erwartungsnutzen des Endvermögens maximieren. Diese Zielformulierung geht auf Bernoulli (Bernoulli, D. 1954) zurück. In Erweiterung des Grundkonzepts wird außerdem angenommen, dass sich die Entscheidungsträger rational im Sinne der von Neumann/Morgenstern-Axiome verhalten (von Neumann, J./Morgenstern, O. 1944).
Das Endvermögen eines Entscheidungsträgers w?1 setzt sich zusammen aus dem Anfangsvermögen w0 und dem unsicheren Portfolio-Einkommen w0 r?p, das funktional von der Allokation des Anfangsvermögens w0 auf die zur Verfügung stehenden Kapitalanlagen abhängt 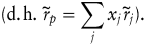 Das Optimierungsproblem des Investors besteht demnach darin, die relativen Portfolio-Anteile xj der zur Verfügung stehenden Kapitalanlagen j=1,...,N so zu wählen, dass der Erwartungsnutzen des Endvermögens maximiert wird. Das Optimierungsproblem des Investors besteht demnach darin, die relativen Portfolio-Anteile xj der zur Verfügung stehenden Kapitalanlagen j=1,...,N so zu wählen, dass der Erwartungsnutzen des Endvermögens maximiert wird.
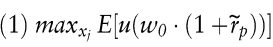
Dabei erfolgt die Formulierung des Endvermögens w?1 unter der impliziten Annahme eines vollkommenen Kapitalmarktes (keine Transaktionskosten oder Steuern, beliebige Teilbarkeit der Kapitalanlagen, vollständige Verfügbarkeit der Erlöse aus Leerverkäufen).
Ökonomisch plausibel und empirisch vertretbar sind des weiteren die Annahmen der Nichtsättigung (u ´ > 0) und der Risikoaversion (u ´ ´< 0) des Entscheidungsträgers.
Die Optimierung kann auch unter diversen Nebenbedingungen erfolgen, die sowohl institutionell bedingt als auch selbst auferlegt sein können. So können beispielsweise Leerverkaufs- bzw. Kreditaufnahmebeschränkungen, d.h. xj ≥ 0 für j E {1, ...,N}, berücksichtigt werden.
Nichtsättigung und Risikoaversion als Eigenschaften der von Neumann/Morgenstern-Nutzenfunktion führen dazu, dass Investoren ceteris paribus Vermögensverteilungen mit höherem erwartetem Endvermögen und niedrigerer Streuung präferieren. Die ausschließliche Berücksichtigung von Erwartungswert und Varianz ist allerdings nur dann ein hinreichendes Kriterium für die Erwartungsnutzenmaximierung, wenn der Erwartungsnutzen eines Investors vollständig durch die beiden ersten Zentralmomente der Vermögensverteilung beschrieben wird.
Um die Plausibilität dieser Annahme besser beurteilen zu können, wird zunächst die Taylor-Erweiterung des Endvermögensnutzens an der Stelle des erwarteten Endvermögens betrachtet, wobei im Folgenden auf die explizite Kennzeichnung von Zufallsvariablen durch das Symbol ~ verzichtet wird:
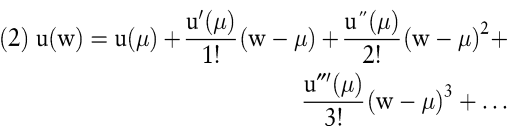
wobei μ = E(w).
Bildet man den Erwartungswert des Nutzens, so entfällt der zweite Term aus (2). Der dritte Term beinhaltet die Varianz, also das zweite zentrale Moment der Vermögensverteilung, die restlichen Terme hängen von den höheren zentralen Momenten der Verteilung ab.
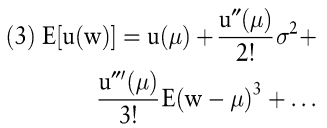
In zwei Fällen ist die Reduktion auf die ersten beiden zentralen Momente eine zulässige Vereinfachung des Präferenzfunktionals:
1) Im ersten Fall wird von einer quadratischen Nutzenfunktion in der allgemeinen Form
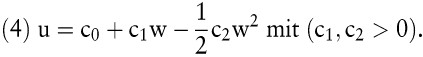
ausgegangen. Da die Ableitungen dritter sowie höherer Ordnung bei quadratischen Nutzenfunktionen gleich Null sind, kann folglich (3) in Abhängigkeit von Erwartungswert und Varianz des Vermögens geschrieben werden als
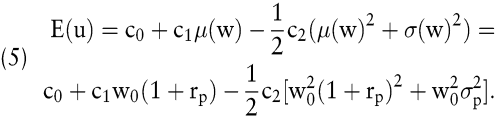
Parametrisiert man E(u), so stellt (5) eine Schar von Indifferenzkurven im μ/σ-Raum dar. Leider hat die quadratische Nutzenfunktion einige ökonomisch unplausible Eigenschaften:
(a) Der Grenznutzen des Portfolio-Einkommens wird negativ falls c1/c2 < w. In diesem Bereich stellt Einkommen ein inferiores Gut dar.
(b) Das Pratt-Maß für die lokale absolute und relative Risikoaversion ist bei quadratischen Nutzenfunktionen eine steigende Funktion des Vermögens (Pratt, J. W. 1964).
2) Im zweiten Fall wird von einer Normalverteilung des Portfolio-Einkommens ausgegangen.
Hinreichende Bedingung für ein normalverteiltes Portfolio-Einkommen ist, dass die Rendite-Verteilungen der einzelnen Kapital-Anlagen im Portfolio multivariat normalverteilt sind.
Wegen der Symmetrie der Normalverteilung verschwinden alle ungeraden höheren Momente in (3) und die geraden höheren Momente lassen sich als Funktionen von E(w) und σ(w) ausdrücken. Daraus folgt, dass die Präferenzen des Investors vollständig als Indifferenzkurvenschar in der μ/σ-Ebene dargestellt werden können. Wie Tobin (Tobin, J. 1958) zeigt, verlaufen die Iso-Nutzen-Linien bei Annahme von Nichtsättigung und Risikoaversion des Investors konvex zum Ursprung. 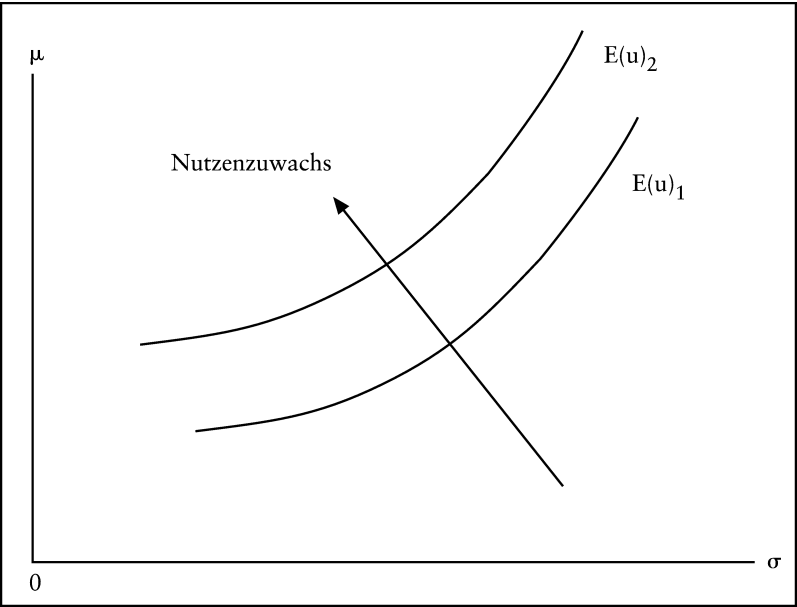
Abb. 1: Indifferenzkurven eines risikoaversen Investors mit rationalen Präferenzen im μ/σ-Raum
Die Annahme multivariater Normalverteilung der Renditen erweist sich als unplausibel und empirisch kaum haltbar. Renditen können zwar unendlich groß werden, aber selbst bei Anlageformen mit unbeschränkter Haftung gibt es eine Renditeuntergrenze (das Vermögen des Investors). Bei Kapitalanlagen mit beschränkter Haftung (z.B. Aktien) beträgt die Renditeuntergrenze – 100%. Die Einkommensverteilungen einzelner Kapitalanlagen sind somit keineswegs symmetrisch, sondern tendenziell rechtsschief. Statistisch liegt Rechtsschiefe bei einem positiven dritten zentralen Moment einer Verteilung vor. Für Aktienrenditen konnte Rechtsschiefe in zahlreichen empirischen Untersuchungen nachgewiesen werden (z.B. Fama, E. F. 1965). Über längere Zeiträume betrachtet entsprechen die Renditen von Aktien eher einer Log-Normalverteilung, denn einer Normalverteilung. Fama (Fama, E. F. 1965) stellt auch für tägliche Aktienrenditen Abweichungen von der Normalverteilungsannahme fest. Zwar kann er die Symmetrie-Hypothese in diesem Fall nicht ablehnen, jedoch weicht das vierte zentrale Moment der Renditeverteilung (die Wölbung) signifikant von der Normalverteilung ab. Die empirischen Verteilungen weisen so genannte \'fat tails\' auf, d.h. im Vergleich zur Normalverteilung verlagert sich Wahrscheinlichkeitsmasse vom Zentrum der Verteilung in die Außenbereiche der Verteilung. Man spricht in diesem Zusammenhang von einer Pareto-Verteilung. Dadurch entsteht das Problem infiniter Varianzen. Dieses macht es für den Investor unmöglich, Portfolio-Entscheidungen anhand des μ/σ-Kriteriums zu treffen. Fama zeigt jedoch, dass bei Stabilität der Renditeverteilung auch andere Dispersionsmaße zur Portfolio-Selektion im Sinne von Markowitz herangezogen werden können.
Bereits Markowitz (Markowitz, 1952) beurteilt jedoch die Annahme stabiler Verteilungen als besonders kritisch, da sich selbst bei kurzen Anlagezeiträumen der Informationsstand des Investors und damit seine Erwartungshaltung bzgl. Rendite und Risiko der Anlagealternativen verändern kann. Eine Verteilung wird als stabil bezeichnet, falls sich ihre Parameter während der Messperiode (also hier während des Anlagezeitraums) nicht verändern. Parameterinstabilitäten lassen sich mithilfe neuerer ökonometrischer Verfahren, wie z.B. mit ARCH- und GARCH-Modellen (Engle, R. 1982; Bollerslev, T. 1987) abbilden. Mit ihrer Hilfe lässt sich beispielsweise das empirische Phänomen des Volatilitäts-Clustering (d.h. die Persistenz der Volatilität) an Finanzmärkten beschreiben.
Eine weitere hinreichende Bedingung für die Annahme eines normalverteilten Portfolio-Einkommens ist erfüllt, falls die Investoren \'wohl diversifizierte Portfolios\' halten. Ein Portfolio wird als \'wohl diversifiziert\' bezeichnet, falls die Anwendung des \'Zentralen Grenzwertsatzes\' (ZGWS) gerechtfertigt ist (Hirshleifer, J./Riley, J. G. 1992). Der ZGWS besagt, dass die Verteilung einer Summe von identisch verteilten Zufallsvariablen, falls diese nicht perfekt miteinander korrelieren, mit zunehmender Summandenzahl gegen eine Normalverteilung konvergiert.
Da weder von strikter stochastischer Unabhängigkeit, noch von identischen Renditeverteilungen ausgegangen werden kann, können \'wohl diversifizierte\' Portfolios nur approximativ gegeben sein. Tendenziell werden die höheren zentralen Momente von Renditeverteilungen durch Bildung näherungsweise \'wohl diversifizierter\' Portfolios eliminiert. Der ausserordentlich hohe Portfolio-Anteil des Humankapitals, sowie die empirisch beobachtbare Präferenz für Lotterien mit rechtsschiefen Verteilungen spricht eher gegen die Annahme, dass Investoren \'wohl diversifizierte\' Portfolios halten.
IV. Effiziente Portfolios
Akzeptiert man, dass Investoren (i) den Erwartungsnutzen des Endvermögens maximieren, (ii) Nutzenfunktionen mit den üblichen Eigenschaften u ´ > 0 (Nichtsättigung) und u ´ ´ < 0 (risikoaversion) besitzen und dass (iii) ihre Präferenzen vollständig im μ/σ-Raum abgebildet werden können, so stellt sich die Frage, welches Portfolio sie aus der Menge aller erreichbaren Portfolios wählen.
Der entscheidende Schritt von Markowitz (Markowitz, 1952) bestand in der Reduzierung des Portfolio-Selektions-Problems des Investors auf die Teilmenge effizienter Portfolios. Nur aus dieser Teilmenge wählt der Investor sein optimales Portfolio. Mathematisch erfolgt bei gegebener Portfoliorendite eine Minimierung der Varianz
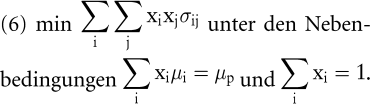
Die Lösung erfolgt mithilfe der Linearen Programmierung. Daraus ergibt sich die im μ/σ-Raum dargestellte Hyperbel der Minimum-Varianz-Portfolios (Möglichkeitslinie). M kennzeichnet dabei das global varianzminimale Portfolio. Effizient ist nur der obere Ast dieser Hyperbel, der die μ/σ-effizienten Portfolios repräsentiert (siehe Abb. 2). μ/σ-effizient sind die Portfolios, die bei gegebener Varianz die höchstmögliche erwartete Rendite bieten. 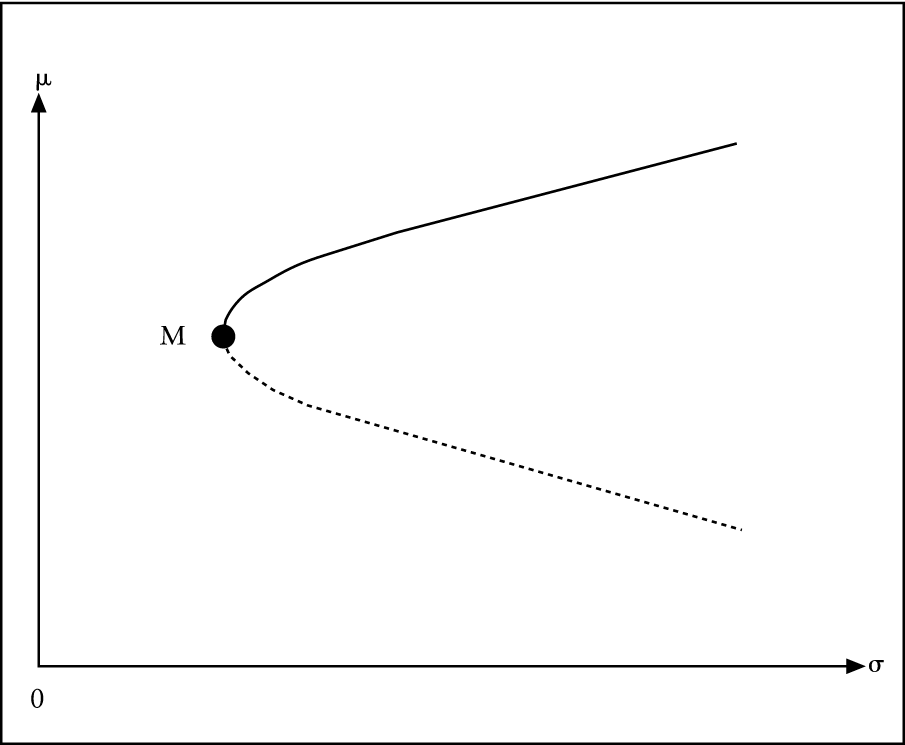
Abb. 2: Die Menge effizienter Portfolios im μ/σ-Raum
Existiert zusätzlich eine risikolose Kapital-Anlage (σ=0) mit unbeschränkten Leerverkaufsmöglichkeiten, so besteht die Menge der effizienten Portfolios aus Linearkombinationen zwischen der risikolosen Kapital-Anlage f und dem Tangential-Portfolio T, dem nunmehr einzigen effizienten Portfolio, das ausschließlich aus risikobehafteten Kapitalanlagen besteht. Die erwartete Rendite eines effizienten Portfolios lässt sich in diesem Fall schreiben als
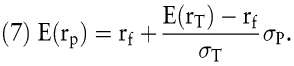
Die Linearität effizienter Portfolios im μ/σ-Raum hat weitreichende Konsequenzen. So ist die optimale Mischung risikobehafteter Kapitalanlagen eindeutig durch das Tangential-Portfolio T bestimmt. Insbesondere ist das Verhältnis der Portfolio-Anteile in T unabhängig vom Vermögen des Investors, also unabhängig von der lokalen Risikoaversion nach Pratt (Pratt, J. W. 1964) und außerdem unabhängig von der globalen Risikotoleranz des Investors. Betrachtet man z.B. zwei Investoren A und B mit unterschiedlicher globaler Risikotoleranz (siehe Abb. 3), so halten beide das Tangential-Portfolio T. Die unterschiedliche Risikoneigung beider Investoren kommt ausschließlich im Anteil von T an den Gesamt-Portfolios von A und B zum Ausdruck. Während A positive Anteile in der risikolosen Kapital-Anlage f und dem Tangential-Portfolio T hält, verkauft B Anteile in der risikolosen Anlage leer und investiert den Erlös in T. Investor A wird daher auch häufig als Gläubiger und Investor B als Schuldner charakterisiert. Die Unabhängigkeit des optimalen Portfolios risikobehafteter Kapitalanlagen von individuellen Investorpräferenzen wird auch als \'Two-Fund-Separation\' bezeichnet und geht auf Tobin (Tobin, J. 1958) zurück.
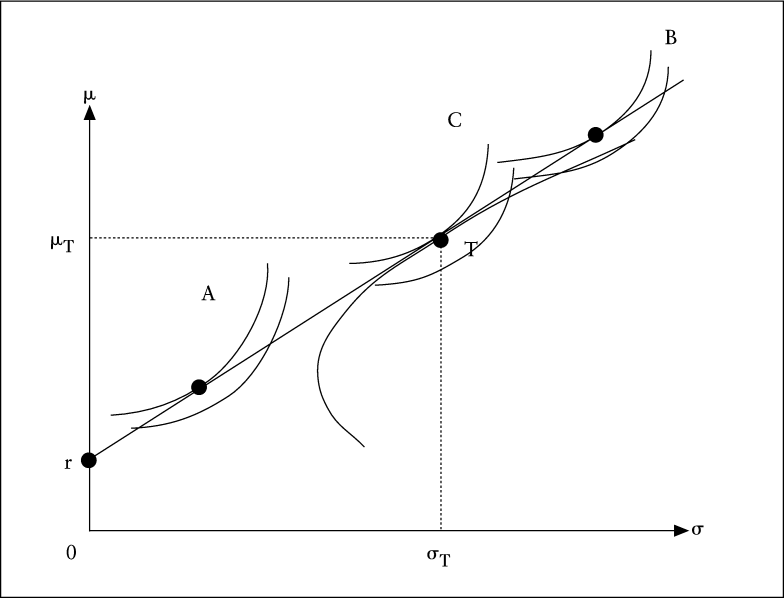
Abb. 3: Menge effizienter Portfolios bei Existenz einer risikolosen Kapital-Anlage
An dieser Stelle sei auf die pareto-verbessernde Wirkung von vollkommenen Kapitalmärkten, d.h. insbesondere von unbeschränkten risikolosen Geldaufnahme- bzw. Anlagemöglichkeiten hingewiesen. In diesem Fall stellen sich, wie in Abb. 3 erkennbar, sowohl Investor A als auch Investor B besser. Beide erreichen höhere Nutzenindifferenzkurven. Gleichzeitig kann sich niemand verschlechtern. Investor C kann als marginaler Investor angesehen werden, da er sich durch die Einführung der risikolosen Kapitalanlage nicht verbessert. Er ist indifferent bzgl. der Existenz von rf, da er 100% seines Budgets in das Tangential-Portfolio investiert, also weder Schuldner noch Gläubiger ist.
V. Erweiterungen der Portfoliotheorie
1. Marktgleichgewicht bei homogenen Erwartungen der Investoren
Das Tangential-Portfolio in Abb. 3 erhält weitergehende Interpretierbarkeit, falls angenommen wird, dass alle Investoren homogene Erwartungen haben, sich also der gleichen Menge μ/σ-dominanter Portfolios gegenübersehen. In diesem Fall wählen alle Investoren das gleiche Portfolio aus risikobehafteten Anlagen. Da im Marktgleichgewicht alle Kapitalanlagen gehalten werden müssen, handelt es sich bei diesem Portfolio um das Markt-Portfolio (MP). Alle Kapitalanlagen gehen im Verhältnis ihres Marktwerts zum Gesamtmarktwert in das MP ein. Die Anteile sind daher stets positiv. Da alle Marktteilnehmer ein Portfolio mit ausschließlich positiven Anteilswerten nachfragen, besteht keinerlei Interesse an Leerverkäufen risikobehafteter Kapitalanlagen.
Die wichtigste Implikation des \'Mutual-Fund-Theorems\' liegt im Bereich eines einheitlichen Marktpreises des Risikos, der durch die Steigung der Effizienzlinie in (7) determiniert ist. Diese Effizienzlinie wird als Kapitalmarktlinie bezeichnet. Durch den einheitlichen Marktpreis des Risikos werden ähnlich wie bei der Fisher-Separation (Fisher, I. 1930) Investitionsentscheidungen an Agenten delegierbar. Sie hängen nicht von den Risikopräferenzen der Kapitalgeber ab. Im Marktgleichgewicht entsprechen alle subjektiven marginalen Raten der Substitution (MRS) bezüglich μ/σ dem Marktpreis des Risikos.
Aus der zusätzlichen Bedingung, dass im Marktgleichgewicht die Überschussnachfragen nach risikobehafteten Anlagen gleich Null sein müssen, lässt sich zudem die Preisrelation des Capital Asset Pricing Model (Sharpe, W. F. 1964) herleiten, die auch als Wertpapiermarktlinie bezeichnet wird.
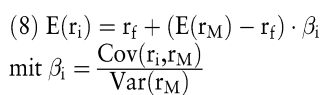
Im Marktgleichgewicht ist die erwartete Rendite einer Kapitalanlage i eine lineare Funktion ihres Kovarianzrisikos. Dieses Kovarianzrisiko wird auch als systematisches Risiko einer Kapitalanlage bezeichnet. Das systematische Risiko ist der Teil des Gesamtrisikos einer Kapitalanlage, der nicht durch die Bildung eines \'wohl diversifizierten\' Portfolios eliminiert werden kann. Aufgrund der Zerlegbarkeit der Gesamtvarianz in systematische und unsystematische Bestandteile kann der renditegenerierende Prozess einer Kapitalanlage mithilfe des folgenden linearen Modells beschrieben werden:
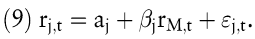
Dieses lineare Modell wird auch als Markt-Modell bzw. als \'Single-Index-Model\' bezeichnet und zur Beschreibung des empirischen Zusammenhangs zwischen der Rendite einer Kapitalanlage j und der Marktrendite verwendet. Der Regressionsparameter βj entspricht dem CAPM-Beta.
Im CAPM-Marktgleichgewicht muss gelten, dass die Residualrenditen des Markt-Modells in einer Querschnittsbetrachtung über alle Kapitalanlagen unkorreliert sein müssen. Die Varianz/Kovarianz-Matrix der Portfolio-Residualrenditen weist daher die so genannte Diagonaleigenschaft auf, d.h. die Matrix besitzt nur auf ihrer Hauptdiagonalen von Null abweichende Einträge.
Durch Bildung eines \'wohl-diversifizierten\' Portfolios geht der Residualvarianzanteil gegen Null. Bei endlicher Anzahl von Kapitalanlagen verschwindet die Residualvarianz eines Portfolios somit zwar nicht vollständig, wird jedoch schon ab N=10 vernachlässigbar klein. Folglich besteht, bei hinreichender Diversifikation, die Portfolio-Varianz zumindest approximativ ausschließlich aus systematischen Bestandteilen, nämlich den mit ihren Portfolio-Anteilen gewichteten Kovarianzrisiken. Durch Anwendung des Diagonal-Modells lassen sich somit zumindest annähernd effiziente Portfolios bestimmen.
Ein praktischer Vorteil dieser Vorgehensweise liegt in einer erheblichen Verminderung des Schätz- und Rechenaufwandes bei der Portfolio-Optimierung. Bei Anwendung der Markowitz-Methode zur Bestimmung von Minimum-Varianz-Portfolios erweist sich bereits die Parameterschätzung bei hinreichend großer Anzahl zur Verfügung stehender Anlagealternativen als äußerst komplexes Problem. Im N-Anlagen-Fall hat der Investor neben N Erwartungswerten und N Varianzen noch (N2-N)/2 Kovarianzen zu schätzen. Hinzu kommt, dass für jede vorgegebene erwartete Rendite ein konvexes Programmierungsproblem mit mindestens 2 Nebenbedingungen zu lösen ist. Kommen Leerverkaufsbeschränkungen hinzu, so wächst die Anzahl der Nebenbedingungen um die Anzahl der nicht leerverkaufbaren Anlagealternativen. Zieht man die Vielfalt der in der Realität existierenden Anlagealternativen in Betracht, so stellt die Bestimmung minimum-varianz-effizienter Portfolios eine kaum lösbare Aufgabe für den Investor dar.
Neben der nur approximativen Bestimmbarkeit effizienter Portfolios besteht ein weiteres Problem des Markt-Modells darin, dass das Markt-Portfolio im Praxis-Einsatz durch einen Markt-Index abgebildet wird, der jeweils nur eine Teilmenge der Gesamtpopulation von Kapitalanlagen repräsentiert.
Der hier vorgestellte μ/σ-Ansatz der Portfolio-Selektion und seine Erweiterungen sind sowohl aus normativer wie auch aus deskriptiver Sicht nur dann akzeptabel, falls seine Prämissen als zulässige Vereinfachungen der Realität akzeptiert werden können. Hierzu ist sowohl die Konfrontation der Modellaussagen mit der Empirie, als auch die Frage nach der Robustheit der Theorie-Implikationen bei Aufweichung einiger restriktiver Annahmen notwendig. Im Rahmen dieser Abhandlung wird nur kurz auf Letzteres eingegangen. Für eine Zusammenfassung empirischer Ergebnisse kann auf Copeland/Weston (Copeland, T. E./Weston, J. F. 1988), Fama (Fama, 1991) und Campbell et al. (Campbell, /Lo, /MacKinlay, 1997) verwiesen werden.
Die bei der Herleitung der \'Two-Fund-Separation\' und des CAPM gemachte Annahme einer risikolosen und unbeschränkten Kapitalanlagemöglichkeit widerspricht unmittelbar der empirischen Beobachtung. Sie ist schon alleine deshalb unplausibel, weil bei der gleichzeitig gesetzten Prämisse multivariat normalverteilter Renditen immer eine positive Konkurswahrscheinlichkeit des Investors gegeben ist. Des weiteren ist die Einheitlichkeit des risikolosen Zinssatzes aufgrund von Marktunvollkommenheiten, z.B. Transaktionskosten, zumindest nicht für alle Marktteilnehmer gegeben. Trotzdem lassen sich Separationseigenschaft und CAPM-Preisrelation bei Existenz eines so genannten Zero-Beta-Portfolios retten (Black, F. 1972). Ein Zero-Beta-Portfolio ist ein Portfolio, dessen Rendite stochastisch unabhängig von der Marktrendite ist. Black zeigt die Existenz und die Eindeutigkeit eines solchen Portfolios. Bildet man nun Linear-Kombinationen zwischen dem Zero-Beta-Portfolio und dem Markt-Portfolio, so erhält man eine Effizienzlinie im μ/σ-Raum, die sich von der Kapitalmarktlinie nur durch die Substitution der risikolosen Kapitalanlage durch das Zero-Beta-Portfolio unterscheidet. Ein einheitlicher Marktpreis des Risikos existiert in diesem Fall allerdings nur unter der Prämisse unbeschränkter Leerverkaufsmöglichkeiten für das Zero-Beta-Portfolio.
Lintner zeigte, dass die wesentlichen Implikationen des CAPM auch bei heterogenen Erwartungen der Marktteilnehmer erhalten bleiben (Lintner, J. 1969). Der einzige Unterschied zum Ursprungsmodell besteht bei Lintner darin, dass Erwartungswerte und Kovarianzen komplexe gewichtete Durchschnitte der Investoren-Erwartungen sind. Allerdings ist unmittelbar einsichtig, dass im Fall heterogener Erwartungen die Separationseigenschaft verloren geht, d.h. nicht alle Investoren das gleiche Portfolio aus risikobehafteten Kapitalanlagen wählen. Folglich ist das Markt-Portfolio nicht mehr notwendigerweise effizient. Dieser Umstand stellt die empirische Testbarkeit des CAPM ernsthaft in Frage (Roll, R. 1977). Als weitere Implikation des Lintner-CAPM besitzen Marktpreise für die Marktteilnehmer Informationscharakter. Hierzu entstand ausgehend von Grossman (Grossman, S. J. 1976) und Grossman/Stiglitz (Grossman, S. J./Stiglitz, J. E. 1976) eine umfangreiche Literatur zur Verarbeitung von Informationen in Kapitalmärkten.
4. Mehrperiodige Portfolio-Selektions- und Asset-Pricing-Modelle
Bisher wurde vereinfachend von einem Portfolio-Auswahlproblem mit einperiodigem Entscheidungshorizont des Investors ausgegangen. Diese Myopik könnte unter Umständen die Gültigkeit des vorgestellten μ/σ-Ansatzes in Frage stellen. Es wurden daher Modelle entwickelt, die nicht nur den Erwartungsnutzen des Endvermögens, sondern den Erwartungsnutzen des Lebenszeit-Konsums (inkl. des Erbgutes) maximieren.
Im statischen/einperiodigen Kontext agieren die Entscheider als Maximierer ihres erwarteten Endvermögens. Hier sollte aber beachtet werden, dass das letzte Ziel des Wirtschaftens nicht die Vermögensmaximierung, sondern der Konsum ist. Im einperiodigen Zusammenhang stellt dies kein Problem dar, da implizit die Annahme getroffen wird, dass am Ende der Modellperiode das angesammelte Vermögen konsumiert wird. Im mehrperiodigen Kontext ändert sich die Situation: Die Unterscheidung zwischen der Ausrichtung der individuellen Entscheidungen am erwarteten Vermögen oder am optimalen intertemporalen Konsum wird dann relevant.
Merton (Merton, 1971) gelang es nachzuweisen, dass das optimale Portfolio eines Investors, bei kontinuierlicher Portfolio-Revision, die gleiche Separationseigenschaft aufweist wie im Einperioden-Modell von Tobin (Tobin, J. 1958). In einer Erweiterung dieses Ansatzes zeigt Merton (Merton, R. C. 1973), dass bei stochastischer risikoloser Anlage die \'Two-Fund-Separation\' in eine \'Three-Fund-Separation\' übergeht, d.h. dass alle Investoren ihr individuelles Portfolio aus 3 \'Funds\' zusammenstellen, dem Markt-Portfolio, der risikolosen Anlage und einem Hedge-Portfolio, das sie gegen unerwartete Veränderungen des risikolosen Zinssatzes absichert. Für die zusätzliche Statusvariable Unsicherheit des risikolosen Zinses wird ein Risikozuschlag verlangt. Die Interpretation ist jedoch kontraintuitiv in bezug auf das Standard-CAPM, da der Zusammenhang zwischen dem Wert eines Assets und seinem marginalen Beitrag zum Vermögen im intertemporalen CAPM so nicht mehr vorhanden ist.
Das von Breeden (Breeden, D. 1979) entwickelte Konsum-CAPM ist die probate dynamische Formulierung in Analogie zum statischen Modell des Standard-CAPM. Das Konsum-CAPM setzt um, dass im intertemporalen Zusammenhang die entscheidende Größe der individuelle intertemporale Konsumplan ist. Damit kann der Wert eines Assets nicht mehr von seinem marginalen Beitrag zum Endvermögen (einperiodig), sondern von seinem marginalen Risikobeitrag zum Konsumplan abhängt. Die Wachstumsrate des Pro-Kopf-Konsums ersetzt die Rendite des Marktportefeuilles als determinierende Variable der Gleichgewichtsrenditen der Assets, diese werden also in Abhängigkeit ihrer Kovarianz mit dem aggregierten Konsum bepreist. Dies ergibt dann als Konsequenz in Analogie zum Standard-CAPM das Konsum-Beta als erklärende Variable der Assetrenditen.
VI. Grenzen der Portfoliotheorie
Die Portfoliotheorie hat für ein halbes Jahrhundert die empirische und theoretische Kaptalmarktforschung beherrscht. Sie hat in dieser Zeit zahlreiche Erweiterungen und Verfeinerungen erfahren, durch die z.B. auch beschränkt rationales Verhalten über so genanntes Noise Trading (Röckemann, Ch. 1995; von Heyle, D. 1995) in die ansonsten auf der Prämisse vollkommener Märkte basierende Postfoliotheorie eingebaut wurde. Zunehmend wird in der Kapitalmarktforschung aber herausgearbeitet, dass zwischen den Gesellschaften und Managern eines Unternehmens Interessenskonflikte auftreten, dass Informationsassymetrien die Finanzierung behindern und Anleger sentimental (Gerke, 2000) statt rational handeln.
Im Rahmen von Behavioral Finance-Ansätzen (Shefrin, H. 2000; DeBondt, W. F. M./Thaler, R. H. 1995) wird die Irrationalität der Anleger betont. Insbesondere kurzfristig handeln zahlreiche Investoren irrational. Sie folgen mit so genanntem Herdenverhalten (Devenow, A./Welch, I. 1996) Zeittrends, verhalten sich in Verlustsituationen anders als in Gewinnsituationen (siehe zum Dispositionseffekt Shefrin, H./Statman, M. 1985; Gerke, W./Bienert, H. 1993). Überreaktionen prägen die Marktpreise (Shiller, R. J. 2000; Bank, M. 2001). Die Behavioral Finance-Ansätze werden aber immer den Nachteil aufweisen, dass sie die Stringenz und Geschlossenheit der Portfoliotheorie in ihren Aussagen nicht erreichen können.
Literatur:
Bank, M. : Behavioral Finance und Börsenkursmanipulation, unveröffentlichte Habilitationsschrift, Nürnberg 2001
Bernoulli, D. : Exposition of a New Theory on the Measurement of Risk, Original aus dem Jahre 1738, übersetzt von Sommer, L., in: Econometrica 1954, S. 23 – 36
Black, F. : Capital Market Equilibrium with Restricted Borrowing, in: JBus. 1972, S. 444 – 455
Bollerslev, T. : A Conditional Heteroscedastic Time Series Model for Speculative Prices and Rates of Return, in: REStat. 1987, S. 542 – 547
Breeden, D. : An Intertemporal Asset Pricing Model with Stochastic Consumption and Investment Opportunities, in: Journal of Financial Economics, 1979, S. 265 – 296
Campbell, J. Y./Lo, A. W./MacKinlay, : The Econometrics of Financial Markets, Princeton, 1997
Copeland, T. E./Weston, J. F. : Financial Theory and Corporate Policy, 3. A., Reading (MA) 1988
DeBondt, W. F. M./Thaler, R. H. : Financial Decision-Making in Markets and Firms: A Behavioral Perspective, in: Finance, Handbooks in Operations Research and Management Science, hrsg. v. Jarrow, R. A. et al., Amsterdam 1995, S. 385 – 410
Devenow, A./Welch, I. : Rational herding in financial economics, in: European Economic Review 40, 1996, S. 603 – 615
Engle, R. : Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of U. K. Inflation, in: Econometrica 1982, S. 987 – 1008
Fama, E. F. : The Behavior of Stock Market Prices, in: JBus. 1965, S. 34 – 105
Fama, E. F. : Efficient Capital Markets: II, in: JoF 1991, S. 1575 – 1617
Fisher, I. : The Theory of Interest, New York 1930
Freund, R. : The Introduction of Risk into a Programming Model, in: ENM 1956, S. 253 – 263
Gerke, W. : Portefeuille-Theorie, in: Handwörterbuch der Betriebswirtschaft, 5. A., Teilband 2, hrsg. v. Wittmann, W./Kern, W./Köhler, R./Küpper, H. U./v. Wysocki, K., Stuttgart 1993, S. 3263 – 3273
Gerke, W./Bienert, H. : Überprüfung des Dispositionseffektes und seiner Auswirkungen in computerisierten Börsenexperimenten, in: Zeitschrift für betriebswirtschaftliche Forschung, Sonderheft 31, 1993, S. 169 – 194
Gerke, W. : Herrschaft der Androiden? Konsequenzen der Kapitalmarkttheorie für das Anlegerverhalten, in: Psychologie für Börsenprofis, hrsg. v. Jünemann, /Schellenberger, D., Stuttgart 2000, S. 21 – 46
Gerke, W./Bank, M. : Finanzierung, Stuttgart, 1998
Grossman, S. J. : On the Efficiency of Competitive Stock Markets where Traders have Diverse Information, in: Journal of Finance, 1976, S. 573 – 585
Grossman, S. J./Stiglitz, J. E. : Information and Competitive Price Systems, in: American Economic Review, 1976, S. 247 – 253
Hirshleifer, J./Riley, J. G. : The Analytics of Uncertainty and Information, Cambridge 1992
Lintner, J. : The Aggregation of Investor\'s Diverse Judgements and Preferences in Purely Competitive Security Markets, in: Journal of Financial and Quantitative Analysis 1969, S. 347 – 400
Markowitz, H. : Portfolio Selection, in: JoF 1952, S. 77 – 91
Markowitz, H. : Portfolio Selection: Efficient Diversification of Investments, Yale 1959
Merton, R. C. : Optimum Consumption and Portfolio Rules in a Continuous-time Model, in: JETheory 1971, S. 373 – 413
Merton, R. C. : An Analytic Derivation of the Efficient Portfolio Frontier, in: Journal of Financial and Quantitative Analysis 1972, S. 1851-1872
Merton, R. C. : An Intertemporal Capital Asset Pricing Model, in: ENM 1973, S. 867 – 888
Pratt, J. W. : Risk Aversion in the Small and in the Large, in: ENM 1964, S. 122 – 136
Röckemann, Ch. : Börsendienste und Anlegerverhalten: ein empirischer Beitrag zum noise trading, Diss., Wiesbaden 1995
Roll, R. : A Critique of the Asset Pricing Theory\'s Tests, in: JFE 1977, S. 129 – 176
Roy, A. : Safety First and the Holding of Assets, in: ENM 1952, S. 431 – 449
Samuelson, P. A. : Lifetime Portfolio Selection by Dynamic Stochastic Programming, in: REStat. 1969, S. 239 – 246
Samuelson, P. A. : The Fundamental Approximation Theorem of Portfolio Analysis in Terms of Means, Variances and Higher Moments, in: REStud. 1970, S. 537 – 542
Sharpe, W. F. : Capital Asset Prices: A Theory of Market Equilibrium under Conditions of Risk, in: JoF 1964, S. 425 – 442
Shefrin, H./Statman, M. : The Disposition of Sell Winners too Early and Ride Losers too Long: Theory and Evidence, in: JoF, Vol. 40, 1985, S. 777 – 790
Shefrin, H. : Beyond Greed and Fear: understanding behavioral finance and the psychology of investing, 2000
Shiller, R. J. : Irrational Exuberance, Princeton 2000
Tobin, J. : Liquidity Preference as a Behavior Towards Risk, in: REStud. 1958, S. 65 – 86
von Heyle, D. : Noise als finanzwirtschaftliches Problem, Frankfurt a. M. 1995
von Neumann, J./Morgenstern, O. : Theory of Games and Economic Behavior, Princeton 1944
|