|
Unsicherheitstheorie
Inhaltsübersicht
I. Sicherheit versus Unsicherheit
II. Risiko, Ungewissheit, Mischformen
III. Bernoulli-Prinzip versus Shortfall-Ansätze
I. Sicherheit versus Unsicherheit
In der Regel hängen die Konsequenzen wirtschaftlicher Entscheidungen von zukünftigen Entwicklungen ab. Typischerweise sind die zukünftigen Entwicklungen (Verhalten von Konkurrenten und Kunden, Änderungen von Rahmenbedingungen, Kursen, Zinsen etc.) nicht mit Sicherheit vorhersehbar. Bezeichnet man die Nichtexistenz von Sicherheit mit Unsicherheit, so herrscht bei wirtschaftlichen Entscheidungen eine mehr oder weniger ausgeprägte Unsicherheit vor. Der Extremfall der Sicherheit ist entscheidungstheoretisch unproblematisch, es sei denn, die Ergebnisse der Entscheidungen betreffen mehrere Ziele, mehrere Zeitpunkte oder mehrere Personen.
Entscheidungssituationen, bei denen die Ergebnisse „ von Hause aus “ durch eine Zahl (Gewinn, Rendite, Endvermögen etc.) gegeben sind, erweisen sich bei Vorhandensein von Unsicherheit ebenfalls entscheidungstheoretisch als problematisch. Nur durch Zugrundelegung eines geeigneten Entscheidungskriteriums wird die Definition von „ optimal “ ermöglicht sowie eine „ vollständige Hitparade “ aller relevanten Aktionen erreichbar. Auf zwei wichtige Spezialfälle von Unsicherheit, nämlich Risiko und Ungewissheit, geht der nächste Abschnitt ein.
II. Risiko, Ungewissheit, Mischformen
1. Risiko und Ungewissheit
Eine Risikosituation ist dadurch charakterisiert, dass (subjektive oder objektive) Wahrscheinlichkeiten für das Eintreten der verschiedenen Zustände der Realität bekannt sind. Bei einer Ungewissheitssituation sind die Zustandswahrscheinlichkeiten per definitionem nicht bekannt. Die Frage liegt nahe, ob man statt dieser Klassifikation nicht strenger zwischen dem Vorliegen von objektiven oder lediglich von subjektiven Wahrscheinlichkeiten unterscheiden sollte. Mit objektiven Wahrscheinlichkeiten hat man es allerdings nur bei klassischen Glücksspielen (Lotto, Roulette und dgl.) zu tun. Hierbei können die Wahrscheinlichkeiten mittels Symmetrien, Annahmen über die Ordnungsmäßigkeit von Geräten usw. deduziert werden. Da die meisten ökonomisch relevanten Situationen jedoch nicht von diesem Typus sind, müssen die bei praxisrelevanten Entscheidungssituationen benutzten Wahrscheinlichkeiten stets mit einer mehr oder minder großen Subjektivität behaftet sein, auch wenn noch so viele empirische Daten oder Expertenmeinungen die Schätzung bzw. Festlegung der Wahrscheinlichkeiten stützen. Deshalb werden in der Entscheidungstheorie subjektive und objektive Wahrscheinlichkeiten „ gleichberechtigt “ behandelt und stattdessen die beiden polaren Fälle der Risikosituation und der Ungewissheitssituation gemäß obiger Definition unterschieden.
Bezeichnen wir die „ Zustände der Realität “ mit z1, z2,..., so ist der Zustandsraum (= Menge aller relevanten Zustände) durch
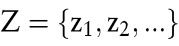
gegeben. Häufig ist es zweckmäßig, einen diskreten (aber sehr umfangreichen) Zustandsraum durch ein Kontinuum zu approximieren. Dabei ist im Falle einer Risikosituation die Wahrscheinlichkeitsverteilung über Z durch eine adäquate Dichte zu beschreiben. Beispielsweise könnte Z die positive Halbachse sein, falls die DAX-Notierungen am Periodenende als Zustände aufgefasst werden.
Vergleicht man die Risikosituation und die Ungewissheitssituation in Bezug auf ihre Bedeutung, so ist festzustellen, dass die Risikosituation in der BWL-Literatur zu Recht als der weitaus wichtigere Fall gilt. In puncto Relevanz der Ungewissheitssituation werden dabei verschiedene Standpunkte vertreten. So liest man bei Eisenführ/Weber (Eisenführ, F./Weber, M. 1999, S. 260): „ Da wir von der betriebswirtschaftlichen Relevanz des Konzepts der Ungewissheit nicht überzeugt sind, wird der Leser in diesem Buch kein Kapitel mit Entscheidungsregeln bei Ungewissheit finden. “ Andere entscheidungstheoretische Lehrbücher enthalten bewusst Abschnitte über Entscheidungen bei Ungewissheit, wobei im Wesentlichen zwei Argumente ins Feld geführt werden:
| - | Versuchspersonen reagieren in Risikosituationen und Ungewissheitssituationen durchaus unterschiedlich (vgl. nachfolgendes Beispiel 1) | | - | Auch partielle Informationen über Zustandswahrscheinlichkeiten führen auf Ungewissheitssituationen (vgl. Beispiel 2 im nächsten Abschnitt). |
Beispiel 1: Präsentiert man Versuchspersonen eine fifty-fifty Lotterie mit den beiden gleich wahrscheinlichen Ergebnissen 0 und 100 und erhebt man den Verkaufspreis (= Sicherheitsäquivalent), zu dem die Probanden ihr Recht zur Teilnahme an der Lotterie abtreten würden, so registriert man variierende Verkaufspreise, die sich jedoch recht ausgeprägt auf den Bereich von 20 bis 50 konzentrieren. Konfrontiert man dieselben Versuchspersonen mit der Ungewissheitssituation, 0 oder 100 zu bekommen (wobei die beiden Wahrscheinlichkeiten gänzlich unbekannt sind), so registriert man deutlich niedrigere Verkaufspreise, die sich etwa im Bereich von 5 bis 25 bewegen.
2. Mischformen zwischen Risiko- und Ungewissheit
Mischformen entstehen, wenn die Zustandswahrscheinlichkeiten
| - | nur partiell bekannt sind oder | | - | als wenig vertrauenswürdig eingestuft werden müssen. |
Zur Erläuterung des ersten Typs diene das Beispiel 2.
Beispiel 2: Für den Absatzmarkt einer neuen Produktvariante sei der dreielementige Zustandsraum relevant mit
z1 = hohe Nachfrage
z2 = mittlere Nachfrage
z3 = niedrige Nachfrage.
Können der Produkt-Manager oder das beauftragte Team nur ermitteln, dass z1 mindestens so wahrscheinlich wie z2 ist und z2 mindestens so wahrscheinlich wie z3 ist, so liegt die partielle Information
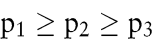
vor, wobei pi = P (Zustand zi tritt ein) bedeutet. Diese Angabe ist zu rudimentär, um die für eine Risikosituation benötigte Wahrscheinlichkeitsverteilung eindeutig festlegen zu können. Beispielsweise sind im Rahmen der gegebenen partiellen Information für (p1, p2, p3) noch
(1, 0, 0) , (½, ¼, ¼) oder (⅓, ⅓, ⅓)
sowie (unendlich) viele weitere Wahrscheinlichkeitsverteilungen möglich.
Mischformen des in Beispiel 2 beschriebenen Typs werden in der Entscheidungstheorie so behandelt, dass alle mit der partiellen Information verträglichen Zustandsverteilungen als neue Zustände aufgefasst werden. Da bezüglich dieser Zustände Ungewissheit vorherrscht, kommen die einschlägigen Entscheidungskriterien bei Ungewissheit (z.B. Maximin-Regel) zum Einsatz. Können alle Restriktionen in Form von linearen Gleichungen oder Ungleichungen formuliert werden, so liegt eine lineare partielle Information (LPI) vor. Im Beispiel 2 liegt eine LPI vor, andere LPI wären beispielsweise p1 = 0,5 oder 0,1 ≤ p3 ≤ 0,2. LPI-Modelle sind bei Kofler/Menges, Kofler, oder Bamberg/Coenenberg detaillierter abgehandelt (Kofler, E./Menges, G. 1976; Kofler, E. 1989; Bamberg, G./Coenenberg, A.G. 2000).
Für reale Entscheidungsträger ist die Wahrnehmung und Handhabung von Wahrscheinlichkeitsverteilungen sicherlich problembehaftet. Daraus entstehen weitere Typen von Mischformen. So könnte (vielleicht aufgrund mangelnder Recherchen oder anderer Ursachen) eine Gleichverteilung über alle Zustände zugrunde gelegt werden, ohne dass der Entscheidungsträger sonderlich davon überzeugt ist, damit die „ wahre Zustandsverteilung “ korrekt erfasst zu haben. In der Entscheidungstheorie wurden Kombinationen aus dem Maximin-Prinzip und dem Bernoulli-Prinzip zur Verarbeitung derartiger (wenig vertrauenswürdiger) Zustandsverteilungen vorgeschlagen. Sie sind als Hodges-Lehmann-Regeln (vgl. Mag, W. 1990 oder Bamberg, G./Coenenberg, A.G. 2000) bekannt geworden.
Zur Beschreibung einer Unsicherheitssituation benötigt man neben der bereits diskutierten Menge Z der relevanten Zustände z noch die Menge A der zur Debatte stehenden Aktionen a sowie eine Ergebnisfunktion g, die für jede Konstellation (a, z) aus ergriffener Aktion a und eingetretenem Zustand z das resultierende Ergebnis g(a, z) quantifiziert. Wenn von einer Reduktion der Unsicherheit die Rede ist, so ist damit auch stets eine Variation des primär gegebenen Aktionenraums A gemeint. Die Entscheidung darüber, ob die (kostenverursachende) Reduktion vorgenommen werden sollte, ist allerdings unter der ursprünglichen Informationsstruktur (Risiko oder Ungewissheit) zu fällen.
Beispiel 3: Kann bei einer Unsicherheitssituation (A, Z, g) der wahre Zustand durch eine kostenintensive Maßnahme (aufwendige Testmarktuntersuchung, teure Materialtests bei Produkthaftungsproblemen etc.) zweifelsfrei ermittelt werden, so ist nach Einsatz dieser Maßnahme die Unsicherheit völlig ausgeschaltet. Bei der Entscheidung, ob sich die Informationsbeschaffung in Anbetracht der entstehenden Kosten lohnt, muss man die bisherigen Aktionen aus A in Konkurrenz zu der zusätzlichen Aktion
a0 = „ Information beschaffen, Kosten tragen, in der resultierende Sicherheitssituation optimal entscheiden “
sehen. Das Entscheidungsproblem mit der so erweiterten Aktionenmenge hat bzgl. Z allerdings noch dieselbe Struktur (Risiko oder Ungewissheit) wie das primäre Problem (ohne Informationsbeschaffungs-Möglichkeit). In der Entscheidungstheorie werden diejenigen Kosten, für die sich die Informationsbeschaffung (gerade noch) lohnt, als Informationswert bezeichnet; er ist in fast allen einschlägigen Lehrbüchern (z.B. Adam, D. 1993; Dinkelbach, W./Kleine, A. 1996; Meyer, R. 1999) beschrieben.
Eine echte Reduktion der primär vorhandenen Unsicherheit ist in Situationen erreichbar, in denen eine Informationsasymmetrie in dem Sinne herrscht, dass andere Personen besser über die Realität informiert sind als der Entscheidungsträger selbst. In derartigen Fällen ist es vielfach möglich und sinnvoll, anreizkompatible Schemata einzusetzen. Hierbei bedeutet anreizkompatibel, dass der Nutzen der besser informierten Seite dadurch maximiert wird, dass sie den Entscheidungsträger wahrheitsgemäß informiert. Wegen Details dieser Schemata, die variable Entlohnungen, Sanktionen, Soll-Ist-Abweichungen und dgl. beinhalten können, sei auf die Literatur verwiesen (z.B. Pfingsten, A. 1989; Ewert, R./Wagenhofer, A. 2000; Bamberg, G./Trost, R. 1998; Krapp, M. 2000).
In diesem Abschnitt werden nur Risikosituationen betrachtet. Die aus einer Aktion a resultierenden Ergebnisse g(a, z) definieren eine Zufallsvariable X. Sofern es der Klarheit dient, werden wir diese Zufallsvariable auch mit Xa bezeichnen.
1. Vor- und Nachteile des Bernoulli-Prinzips
Das (in der Entscheidungstheorie begründete) Bernoulli-Prinzip besagt bekanntlich: Für den Entscheidungsträger existiert eine auf den Ergebnissen x definierte Funktion u (utility-Funktion, Bernoulli-Funktion), sodass die Präferenz zwischen den Aktionen durch den Vergleich der Nutzenerwartungswerte widergespiegelt wird. D.h. die Aktion a wird gegenüber der Aktion b präferiert, wenn zwischen den Nutzenerwartungswerten der zugehörigen Zufallsvariablen Xa und Xb die Ungleichung
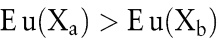
besteht. Bei Indifferenz zwischen a und b gilt statt der Ungleichung die Gleichung. In theoretischen Untersuchungen volks- oder betriebswirtschaftlicher Fragestellungen dient das Bernoulli-Prinzip als unverzichtbares „ Arbeitspferd “ , wenn es beispielsweise darum geht, wie Investoren oder Konsumenten auf bestimmte Änderungen der Rahmenbedingungen reagieren oder wie erfolgsabhängige Entlohnungsschemata wirken. Konkrete Anwendungen sind jedoch nur dann möglich oder relativ unproblematisch, wenn
| - | die Risikonutzenfunktion des Entscheidungsträgers bekannt ist oder ohne großen Aufwand verlässlich zu ermitteln ist, | | - | die Risikonutzenfunktion zwar nicht bekannt ist, jedoch unterstellt werden kann, dass sie zu einer relativ großen und plausiblen Klasse von Funktionen gehört (z.B. monoton wachsend oder zusätzlich noch Risikoaversion beinhaltend). Zudem muss eine Präferenzaussage „ a ist besser als b “ erzielt werden, die in dem Sinne robust ist, dass sie für alle fraglichen Risikonutzenfunktionen gültig ist. In diesem letzeren Fall liegt eine stochastische Dominanz von a über b vom Grade 1 oder 2 vor (vgl. Bamberg, G./Coenenberg, A.G. 2000). |
Damit ist auch bereits angedeutet, dass echte Praxisanwendungen des Bernoulli-Prinzips relativ selten sind. Insbesondere sind sie in der externen Unternehmensrechnung schwer vorstellbar.
2. Vor- und Nachteile von Shortfall-Kriterien
Die Nachteile des (auch in Risikosituationen anwendbaren) Maximin-Prinzips beruhen auf der extrem pessimistischen Grundeinstellung. Die alleinige Orientierung am „ theoretischen Worst Case “ macht es für viele Planungs- und Entscheidungsprobleme untauglich. So würde das Prinzip bei Anlageentscheidungen eine ausschließliche Investition in die risikolose Anlage vorschreiben und damit alle Chancen auf einen höheren Anlageerfolg zunichte machen. Bei der Rückstellungsdotierung würde das Maximin-Prinzip exorbitant hohe Beträge erzwingen. Deshalb ist folgende Abmilderung des Pessimismus und damit verbundene Neudefinition des „ Worst Case “ sinnvoll: Eine (kleine) Wahrscheinlichkeit α wird vorgegeben mit der Eigenschaft, dass der „ Katastrophenfall “ höchstens mit dieser tolerierten Wahrscheinlichkeit α eintreten darf. Der „ Katastrophenfall “ umfasst den „ theoretischen Worst Case “ und entsprechende Nachbarfälle. Diese werden aus der Betrachtung ausgeblendet. Auf die (mit Wahrscheinlichkeit (1 – α) auftretenden) „ Normalfälle “ wird das Maximin-Kriterium angewandt. Registriert man als Ergebnisse Gewinne, so entsprechen Ergebnisse links vom α-Fraktil der Ergebnisverteilung dem Katastrophenfall. Registriert man als Ergebnisse dagegen Verluste oder Schäden, so entsprechen die Ergebnisse rechts vom (1 – α)-Fraktil dem Katastrophenfall (vgl. Abb. 1). Das so abgemilderte Maximin-Prinzip heißt Kataoka-Kriterium (nach Kataoka, S. 1963).
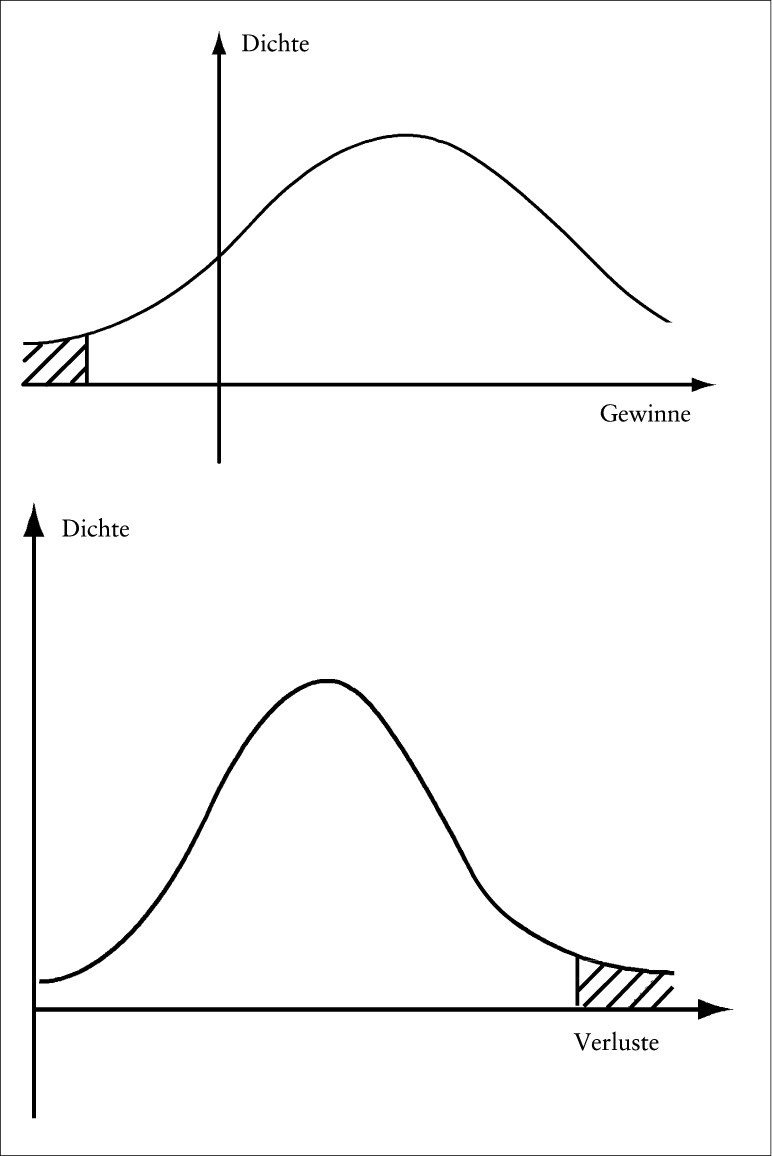
Abb. 1: Beim Kataoka-Kriterium wird eine (kleine) Wahrscheinlichkeit α vorgegeben, mit der der (für die Planung ausgeklammerte) Katastrophenfall eintreten darf. Beurteilungsgröße einer Aktion bzw. der zugehörigen Ergebnisverteilung ist das α -Fraktil (oben in Abb. 1) bzw. das (1 – α)-Fraktil (unten).
Der für die Eigenkapitalunterlegung von Bankaktivitäten bekannte Value at Risk (vgl. z.B. Huschens, S. 1998; Oehler, A./Unser, M. 2001) ist das (1 – α)-Fraktil des Verlusts, wobei üblicherweise α = 1 % und eine Haltedauer von 10 Tagen zugrunde gelegt werden.
Die alleinige Orientierung an einem Verteilungsfraktil ist i. Allg. mit dem Bernoulli-Prinzip unverträglich, worauf bereits Schneeweiß (Schneeweiß, H. 1967, S. 108) deutlich hingewiesen hat. Die Verletzung der dem Bernoulli-Prinzip zugrunde liegenden Rationalitätspostulate kann sich beispielsweise dadurch manifestieren, dass das Kataoka-Kriterium eine Alternative a gegenüber b präferiert, obwohl a von b stochastisch dominiert wird. Kürzlich haben Guthoff/Pfingsten/Wolf anhand von Beispielen demonstriert, dass durch die Verwendung des Value at Risk im Bankbereich suboptimale Entscheidungen resultieren können (Guthoff, A./Pfingsten, A./Wolf, J. 1998).
Diesen Nachteilen stehen als Pro-Argumente gegenüber:
| - | Durch die tolerierte Ausfallwahrscheinlichkeit α ist auch für einen Außenstehenden (wie die Bankenaufsicht) das „ Restrisiko “ gut einschätzbar. | | - | Der Anwender kann die tolerierte Wahrscheinlichkeit α leichter verstehen und spezifizieren als eine Risikonutzenfunktion. | | - | Für gewisse Verteilungsklassen (z.B. Normalverteilungen) verschwinden die oben genannten Inkonsistenzen. |
Die beiden nachfolgenden Beispiele sollen die Wirkungsweise des Kataoka-Kriteriums illustrieren und die Verbesserung gegenüber dem reinen Maximin-Kriterium herausarbeiten.
Beispiel 4: Wird für eine rückstellungsbegründende Bilanzposition angenommen, dass die potenziellen Schadenshöhen logarithmisch normalverteilt sind (vgl. Zimmermann, J. 1991),
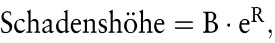
wobei R normalverteilt ist mit den Parametern μ und σ, so ist bei der Spezifizierung μ = – σ2/2 der Faktor B gerade die erwartete Schadenshöhe, z.B. B = 1.000.000. Wählt man als Rückstellungsbetrag a diesen Erwartungswert, so verstößt man gegen das Vorsichtsprinzip. Orientiert man sich am Maximin-Prinzip, so ist kein finiter Rückstellungsbetrag a ausreichend. Nach dem Kataoka-Kriterium erhält man für α = 1 % den Rückstellungsbetrag
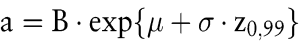 , ,
wobei z0,99 = 2,33 das 99 %-Fraktil der Standardnormalverteilung bedeutet. Setzt man zusätzlich noch σ = 0,1, so errechnet sich die realistische und in 99 % der Fälle ausreichende Rückstellung von
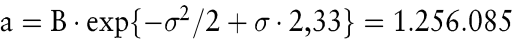 . .
Beispiel 5: Das Standardproblem eines Privatanlegers besteht darin, den Anteil a seines Anfangsvermögens v risikobehaftet (etwa in DAX-Partizipationsscheinen) zu investieren und den restlichen Anteil (1 – a) risikofrei zum Zinssatz r. Beträgt der Anlagehorizont T Perioden, so ist das (stochastische) Endvermögen durch
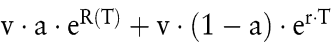
gegeben, wobei die stochastische stetige Rendite R(T) gemäß dem bekannten Black/Scholes-Modell normalverteilt ist mit dem Parametern μ · T und 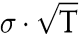 Beschränken wir uns auf a ≤ 1 (d.h. kein Aktienkauf auf Kredit) sowie a ≥ 0 (kein Leerverkauf von Aktien), so schreibt das Maximin-Prinzip a = 0 vor: Alles ist risikolos zu investieren. Demgegenüber ist die Anlage-Empfehlung des Kataoka-Kriteriums weitaus differenzierter. Als α-Fraktil des Endvermögens errechnet man Beschränken wir uns auf a ≤ 1 (d.h. kein Aktienkauf auf Kredit) sowie a ≥ 0 (kein Leerverkauf von Aktien), so schreibt das Maximin-Prinzip a = 0 vor: Alles ist risikolos zu investieren. Demgegenüber ist die Anlage-Empfehlung des Kataoka-Kriteriums weitaus differenzierter. Als α-Fraktil des Endvermögens errechnet man
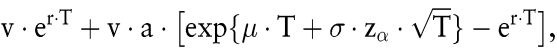
wobei zα wiederum das α-Fraktil der N(0,1)-Verteilung ist. Das Optimum ist leicht abzulesen: Falls der Faktor bei a positiv ist, muss a größtmöglich (d.h. a = 1) sein. Falls der Faktor negativ ist, muss a = 0 sein. Falls der Faktor Null ist, sind alle a gleichwertig. Für den realistischen Fall μ > r ist die Anweisung des Kataoka-Kriteriums durch Abb. 2 illustriert
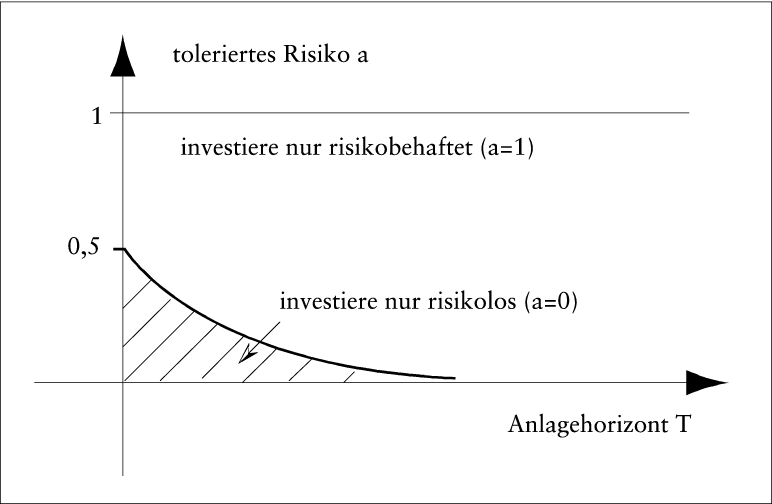
Abb. 2: Das Kataoka-Kriterium schreibt vor, im schraffierten Bereich (d.h. kleine tolerierte Ausfallwahrscheinlichkeit und kleiner Anlagehorizont) das Anfangsvermögen gänzlich risikolos zu investieren. Der größere unschraffierte Bereich entspricht der Anweisung, alles risikobehaftet zu investieren.
Obwohl die Wahrscheinlichkeit α des Kataoka-Kriteriums auch als Shortfall-Wahrscheinlichkeit bezeichnet wird, enthalten die unter der Bezeichnung Shortfall-Kriterien firmierenden Ansätze noch einen zusätzlichen Bestandteil, nämlich ein gesetztes Ziel, das meist als Zielrendite (Benchmark-Rendite) angesetzt wird. Berücksichtigt man im Beispiel 5 zusätzlich die (stetige) Zielrendite r*, so tritt der Shortfall genau dann ein, wenn das Endvermögen kleiner als v · er* · T ist. Die Shortfall-Wahrscheinlichkeit ist demnach
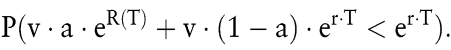
Darf diese höchstens gleich α sein, so ist das Entscheidungsproblem durch das Tripel (α,T,r*) aus toleriertem Risiko, Anlagehorizont und Anlageziel beschrieben, also durch Größen, die auch außerhalb des akademischen Bereichs vermittelbar sind. Wegen der vielfältigen Ausgestaltung der Shortfall-Modelle sei auf die Literatur verwiesen, (z.B. auf Kaduff, J. 1996; Albrecht, P./Maurer, R./Möller, M. 1998; Guthoff, A./Pfingsten, A./Wolf, J. 1998; Bamberg, G./Dorfleitner, G./Lasch, R. 1999; Spremann, K. 2000; Oehler, A./Unser, M. 2001).
Literatur:
Adam, Dietrich : Planung und Entscheidung, Wiesbaden, 3. A., 1993
Albrecht, Peter/Maurer, Raimond/Möller, Matthias : Shortfall-Risiko/Excess-Chance-Entscheidungskalküle: Grundlagen und Beziehungen zum Bernoulli-Prinzip, in: Zeitschrift für Wirtschafts- und Sozialwissenschaften, 1998, S. 249 – 274
Bamberg, Günter/Coenenberg, Adolf G. : Betriebswirtschaftliche Entscheidungslehre, München, 10. A., 2000
Bamberg, Günter/Dorfleitner, Gregor/Lasch, Rainer : Does the Planning Horizon Affect the Portfolio Structure?, in: Classification in the Information Age, hrsg. v. Gaul, Wolfgang/Locarek-Junge, Hermann, New York et al. 1999, S. 110 – 114
Bamberg, Günter/Trost, Ralf : Anreizsysteme und kapitalmarktorientierte Unternehmenssteuerung, in: Rechnungswesen als Instrument für Führungsentscheidungen, hrsg. v. Möller, Hans-Peter/Schmidt, Franz, Stuttgart 1998, S. 91 – 109
Dinkelbach, Werner/Kleine, Andreas : Elemente einer betriebswirtschaftlichen Entscheidungslehre, Berlin et al. 1996
Eisenführ, Franz/Weber, Martin : Rationales Entscheiden, Berlin et al., 3. A., 1999
Ewert, Ralf/Wagenhofer, Alfred : Interne Unternehmensrechnung, Berlin et al., 4. A., 2000
Guthoff, Anja/Pfingsten, Andreas/Wolf, Juliane : Der Einfluß einer Begrenzung des Value at Risk oder des Lower Partial Moment One auf die Risikoübernahme, in: Credit Risk and Value-at-Risk Alternativen, hrsg. v. Oehler, Andreas, Stuttgart 1998, S. 111 – 153
Huschens, Stefan : Messung des besonderen Kursrisikos durch Varianzzerlegung, in: Kredit und Kapital, 1998, S. 567 – 591
Kaduff, Jochen V. : Shortfall-Risk-basierte Portfolio-Strategien, Bern et al. 1996
Kataoka, Shinji : A Stochastic Programming Model, in: Econometrica, Jg. 31, 1963, S. 181 – 196
Kofler, Eduard : Prognosen und Stabilität bei unvollständiger Information, Frankfurt/Main 1989
Kofler, Eduard/Menges, Günter : Entscheidungen bei unvollständiger Information, Berlin et al. 1976
Krapp, Michael : Kooperation und Konkurrenz in Prinzipal-Agent-Beziehungen, Wiesbaden 2000
Mag, Wolfgang : Grundzüge der Entscheidungstheorie, München 1990
Meyer, Roswitha : Entscheidungstheorie, Wiesbaden 1999
Oehler, Andreas/Unser, Matthias : Finanzwirtschaftliches Risikomanagement, Berlin et al. 2001
Pfingsten, Andreas : Der Einsatz von monetären Anreizsystemen in der Planung, in: ZfB, Jg. 59, 1989, S. 1285 – 1296
Schneeweiß, Hans : Entscheidungskriterien bei Risiko, Berlin et al. 1967
Spremann, Klaus : Portfolio-Management, München 2000
Zimmermann, Jochen : Zur Bewertung von Rückstellungen aus risikotheoretischer Sicht, in: ZfbF, Jg. 43, 1991, S. 759 – 782
|